R and herd immunity

Brief summary

The reproduction ratio, R, of a disease (often called the R number in the media) is the average number of people an infected person goes on to infect. If R>1, the epidemic of the disease will spread, the larger the R the quicker it will spread. And if R<1 the disease will die out.

The general idea behind herd immunity is that if you have a population where many people are immune to a disease, the disease can't take hold and grow into an epidemic, thereby protecting those people who aren't immune. The population (perhaps unfortunately called a herd) protects vulnerable individuals.

Two key concepts in epidemiology the reproduction ratio, R, of a disease and herd immunity. As you will find out in this article, the two are closely related.

The basic reproduction ratio, R₀

As we saw in our easy introduction to the reproduction ratio, the value of R, of a disease is the average number of people an infected person goes on to infect. When everyone in the population is susceptible to the disease (say when it first emerges) then this number is also called the basic reproduction ratio, R₀. For seasonal strains of flu, the basic reproduction ratio between 0.9 and 2.1, and for measles it is a whopping 12 to 18.

You can see how a large enough $R_0$ leads to a rapid spread of the disease. For example, if $R_0$ is equal to 2 then a single infected person generates the following growth of new infections:

1st generation: 2 new infections
2nd generation: 4 new infections
3rd generation: 8 new infections
4th generation: 16 new infections....

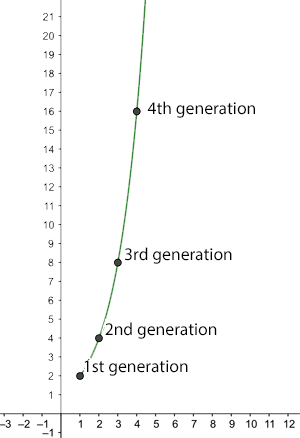
The number of new infections after n generations for R₀=2.

Generally, there are $2^ n$ new infections in the $n$ th round of new infections. Assuming a person is only infectious for a week, at this rate the entire world population (7.8 billion) would be infected after slightly over 32 weeks.

When $R_0$ is less than 1 a very different picture emerges. As an illustration, imagine we have $R_0=0.5.$ Now obviously, an infected person can't go on to infect half a person, but remember that this is an average: it means that 10 people can be assumed to go on to infect 5 others, or that 100 people can be assumed to go on to infect 50 others. To make the numbers simpler, let's assume there are 10,000 infected people to start with, then the number of new infections behaves like this:

1st generation:5,000 new infections
2nd generation: 2,5000 new infections
3rd generation: 1,250 new infections
4th generation: 650 new infections....

Generally, there are $(0.5)^ n$ new infections in the $n$ th round of infections. This number becomes smaller and smaller as the number of generations, $n$ , becomes larger. A dead end for the disease.

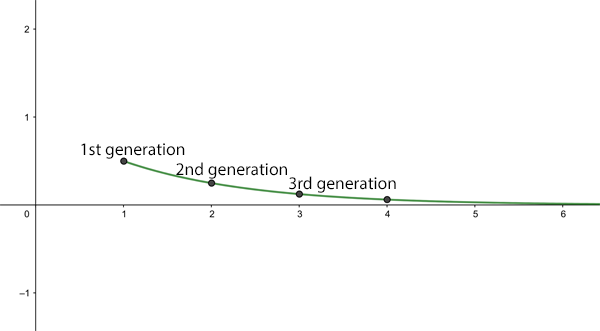
The average number of new infections (in ten thousands) after n generations for R₀=0.5.

What if $R_0=1$ ? In this case the disease will be present in the population, but the number of cases will stay roughly steady over time. When the reproduction ratio is 1 we are not dealing with an epidemic.

The effective reproduction ratio, R

Back to the Epidemiology for beginners collection.

So, given that the $R_0$ of measles, or some strains of seasonal flu, is greater than 1, how come the whole world hasn't been infected with these diseases a long time ago? The reason is that $R_0$ is the average number of people an infected person goes on to infect, given that everyone in the population is susceptible. In real life, this might be the case if someone who has become infected with a disease elsewhere enters a part of the world where the disease has never been seen before, so people don't have immunity and there isn't a vaccine to protect them. An $R_0$ of $2$ then means that, at the beginning, the number of infected people will grow wildly, as we've described above.

However, once a person has recovered from the disease they will (hopefully) gain some immunity. This means that after a while we're not dealing with a totally susceptible population anymore. Indeed, there may be other reasons why some people in the population aren't susceptible. There may be a vaccine available or perhaps behavioural interventions (such as social distancing or infected people isolating) may be reducing the chance of people catching or passing on the disease.

In most real life situations we should be looking at the effective reproduction ratio of the disease, usually denoted by $R$ : the average number an infected person goes on to infect in a population where some people are immune or some other interventions are in place that reduce transmission. Of course $R_0$ and $R$ are related. Writing $s$ for the proportion of the population that is susceptible to catching the disease, we have

$R=sR_0.$

As an example, if only half the population is susceptible, so $s=0.5$ , we have $R=0.5R_0$ . In this case, if $R_0$ is less than or equal to $2$ , then $R$ is less than or equal to $1$ and the disease won’t turn into an epidemic. The ideal aim of any intervention, be it vaccination or social distancing, is to get the effective reproduction ratio down to under 1.

Herd immunity

What does all this have to do with herd immunity? The general idea behind herd immunity is that if you have a population where many people are immune a disease can't take hold and grow into an epidemic, thereby protecting those people who aren't immune. The population (perhaps unfortunately called a herd) protects vulnerable individuals.

So how many people in a population need to be immune to have herd immunity? Imagine a disease has a basic reproduction ratio $R_0$ , which is greater than 1 so an epidemic threatens. As we have seen, if the effective reproduction ratio $R$ is less than 1, then the disease will eventually fizzle out. So to achieve herd immunity we need to somehow get the effective reproduction ratio $R$ to under 1. Since $R=sR_0$ , where $s$ is the proportion of the population that is susceptible, we need

$sR_0<1.$

Rearranging, this gives

$s<1/R_0.$

In other words, we need to get the proportion of susceptible people in the population to under $1/R_0.$ How many people need to be immune to achieve this? If the proportion of susceptible people is $s$ , then the proportion of people who are not susceptible, in other words immune, is $1-s$ . Now

$s<1/R_0$

means

$1-s>1-1/R_0.$

So, to achieve herd immunity we need to make sure that at least a proportion of $1-1/R_0$ of the population is immune. For an $R_0$ of 2, the higher end of the estimates for flu, this means that we need to get at least a proportion of $1-1/2=0.5$ of the population immune, which translates to at least 50%. If there were a vaccine that’s 100% effective, then you’d want to reach at least that proportion with a vaccination programme. For vaccines that aren’t 100% effective you need to adjust the calculation.

The herd immunity calculation for vaccination

As we saw only a proportion of 1-1/R₀ of the population need to be immune to achieve herd immunity, where R₀ is the basic reproduction number of the disease.

If a vaccine has an effectiveness of x%, then this means that only x% of people who receive it are immune. To achieve herd immunity we therefore require that x% of the proportion of people who are vaccinated translate to a proportion of at least 1-1/R₀ of the population. In other words,

$P \times \frac{x}{100} \geq 1-1/R_0,$

where $P$ is the proportion being vaccinated. This gives

$P \geq \frac{100(1-1/R_0)}{x}.$

Substituting $R_0=2.8,$ gives

$P \geq \frac{64}{x}.$

For a vaccine that is 95% effective we therefore need to vaccinate at least a proportion of

$\frac{64}{95} = 0.67$

people, which equates to 67%.

For a vaccine that is 70% effective we need to vaccinate at least a proportion of

$\frac{64}{70}= 0.91$

people, which equates to 91%.

This article is based on a chapter from the book Understanding numbers by the Plus Editors Rachel Thomas and Marianne Freiberger.

This article is part of our collaboration with JUNIPER, the Joint UNIversities Pandemic and Epidemiological Research network. JUNIPER is a collaborative network of researchers from across the UK who work at the interface between mathematical modelling, infectious disease control and public health policy. You can see more content produced with JUNIPER here.