
The risk of death for sickle cell disease
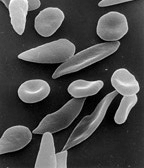
Sickle cell disease deforms red blood cells into a sickle-like shape.
Researchers from Boston University School of Medicine (BUSM) and Boston University School of Public Health (BUSPH) have developed a mathematical method to estimate the severity of sickle cell disease and to predict the risk of death in people with the disease.
The term "sickle cell disease" refers to a whole collection of genetic disorders that cause a patient's red blood cells to deform into a sickle shape. The deformed cells can get stuck in narrow blood vessels and hamper the delivery of oxygen to tissue, causing organ damage or failure, for example stroke.
A major problem with sickle cell disease is that the underlying genetic disorders can express themselves in a variety of different ways — the disease has a wide range of phenotypes. Some people with the disease will experience a whole range of symptoms and health problems — collectively known as clinical events — while others will have few or even none. Some patients die in childhood, while others live to a ripe old age. Blood test results can vary widely between people, and there is a range of genetic variants that impact on the disease. With so many factors to consider, forecasting the severity of the disease in an individual patient and predicting the chance of near-term death is extremely difficult, and at the moment doctors have no satisfactory method for doing so.
The new research, led by Paola Sebastiani and published in the June issue of the journal Blood, addresses this problem. The scientists analysed existing data from 3,380 patients to establish the interdependency of a number of factors. They used a mathematical data mining technique called Bayesian network modelling, named after the eighteenth century mathematician Thomas Bayes.

Thomas Bayes, 1702 - 1761.
Bayes is best-known for his formula for calculating conditional probabilities: the probability that event A will occur, given that event B has occurred. Conditional probabilities are important in medicine, because they give a way of accounting for new evidence and test results. When a doctor first encounters a person with, say, sickle cell disease, there is nothing much to distinguish this individual from others with the disease. In the absence of further information, a general measure of the probability that the person will die prematurely is the proportion of people with the disease that have died prematurely in the past: if half of the patients that were observed in the past died early, then the probability of premature death is 0.5. But once the doctor has observed a clinical event indicating that the patient is already severely damaged by the disease, for example that the patient has had a stroke in the past, this probability may have to be revised. Bayes' theorem provides a way of calculating the revised chance of death (see the tags below for more on Bayes' theorem).
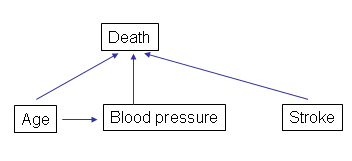
A simplified example of a Bayesian network. It represents the causal relationships between age, blood pressure, stroke and death. Such a network facilitates calculating probabilities of inter-related variables.
In practice doctors treating sickle cell disease have to consider not just one clinical event or test result, but a whole range of them. Updating the chance of near-term death based on a patient profile becomes a complicated business, especially since it is not entirely clear how the various variables impact on each other. This is where Bayesian networks come in. In a Bayesian network each node represents a certain variable and two nodes are linked by an arrow if one impacts on the other. A Bayesian network gives a clear picture of the mutual and hierarchical interdependencies in the system. It comes with probability distributions describing the nature of dependency between nodes, and there are sophisticated computer algorithms for updating the probabilities when the value of one or more variables changes.
To represent the variables associated to disease severity as a Bayesian network, Sebastiani and her colleagues analysed the data from their sample of 3,380 patients. A computer algorithm chomped its way through more than a thousand possible networks, eventually coming up with a particular one which it calculated to be 150 times more likely to be accurate than all others. The nodes of the network represent various clinical events — for example stroke or leg ulceration — laboratory tests, the genotype of the disease, and of course death itself. It describes how the various factors are interconnected and combine to increase the risk of death.
Doctors can enter blood test results and other observations from an individual patient into an online calculator that determines the risk of death within five years.
The researchers used their network to construct a quick-and-easy scoring system to estimate the chance of death within the next five years, based on an individual patient profile. The Sickle Cell Disease Severity Calculator allows doctors to enter information on the variables that, according to the network, significantly impact on the risk of death, for example whether the patient experiences pain or has had a stroke, and the outcome of laboratory tests. A computer algorithm then whizzes through the network, updating the conditional probabilities, and returns a number between 0 and 1 representing the probability of death. "This model can be used to compute a personalised disease severity score allowing therapeutic decisions to be made according to the prognosis," said senior author Martin Steinberg, professor of medicine at BUSM. "The severity score could also serve as an estimate of overall disease severity in genotype-phenotype association studies and provide an additional method to study the complex pathophysiology [the many ways in which the disease can affect the body] of sickle cell disease."