Smale's chaotic horseshoe

On November 30th 1889 the French mathematician Henri Poincaré had a problem. He had been awarded a mathematical prize, offered by no lesser person than King Oscar II of Sweden, for his work on a question that was bothering mathematicians. Using Newton's laws of motion and gravitation you can in theory work out how a number of objects (say stars, planets and moons) should move due to the gravitational pull they exert on each other. If there are only two bodies involved the answer is straight-forward: they move along curves that are easy to describe (ellipses in the case of a planet orbiting a star). The problem was, what happens if you throw a third object into the mix?

Stephen Smale talks about the horseshoe at a (somewhat noisy) press conference at the Heidelberg Laureate forum 2017. Click here to see a video of Smale talking about other aspects of his work, and his career in general.

Things get tricky in this case, but Poincaré did some outstanding work trying to characterise motions that could result in a system with three bodies. The problem he had in November 1889 was that the work contained a mistake. Poincaré did the right thing. He owned up and even paid for the copies of his work that had already been printed. He revised his competition entry, still got the prize, and later wrote more extensively about what the mistake had revealed to him. What it had revealed was the existence of chaos.

Fast forward to 1960 and the beaches of Rio, where the mathematician Stephen Smale was thinking about a problem inspired by the maths of radio waves. The complexity of the problem worried him, especially since he had previously conjectured that there was no such thing as chaos. "I made some pretty bad predictions," he says. "[Norman] Levinson at MIT pointed out that there were these old papers by a pair of English mathematicians [Mary Cartwright and J. L. Littlewood]. They had interesting results which contradicted what I had predicted, and I wanted to understand what they did. So I put what I did in a very geometric context so I could understand it."

The result is now know as Smale's horseshoe map. It beautifully encapsulates how chaotic dynamics can arise in mathematics and goes straight to the heart of the problems Poincaré had encountered when thinking about his three-body problem. "Poincaré got a big mess, and [the horseshoe] put order in the mess."

The horseshoe

Look at the region $D$ shown below, made up of a square $S$ with two rounded-off ends stuck on at the top and at the bottom. Imagine picking this region up, squeezing it in the horizontal direction and stretching it into the vertical direction so that it becomes long and thin, and then bending it round to the right to form a horseshoe. Now place it back down into the original region $D$ as shown. (We could describe this operation using mathematical formulae, but the beautiful thing is that we don’t need to — as you’ll see, the essence of the dynamics can be captured conceptually.)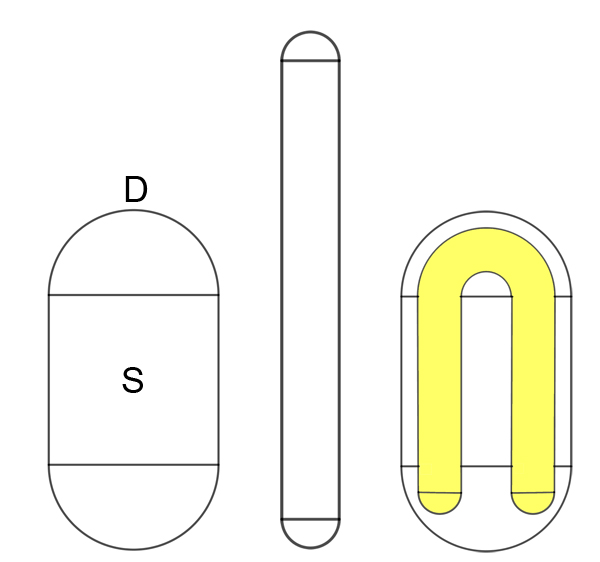

The horseshoe map.

Since the horseshoe is part of the original region $D$ we can ask what happens to it when we perform the squeezing, stretching and bending operation on $D$ again. This squeezes and stretches the horseshoe and then folds it into a "four-stranded" horseshoe sitting within the simple horseshoe.

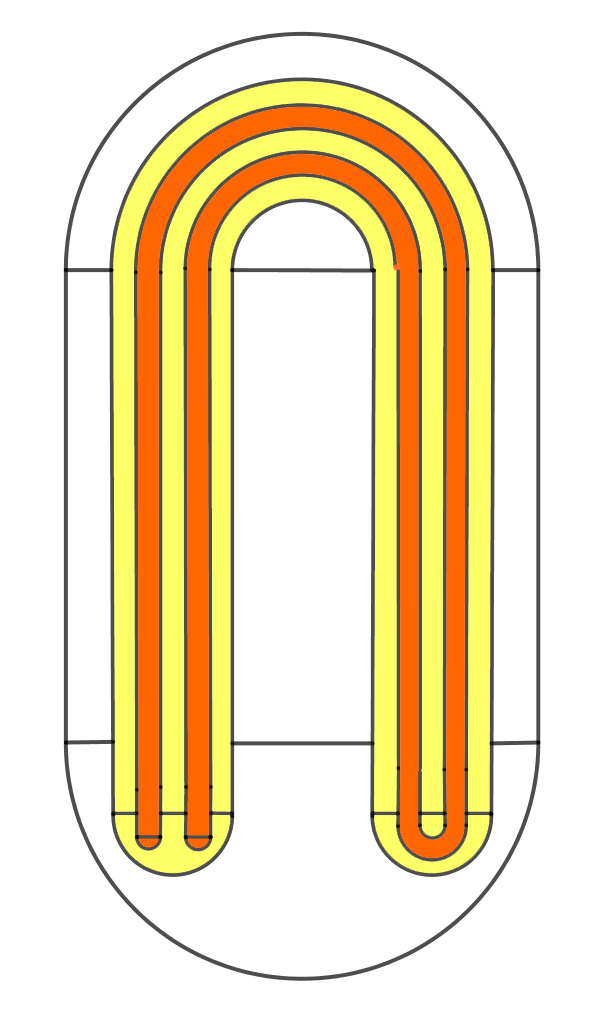
Applying the horseshoe map twice to the region D gives a folded horseshoe.

Performing the operation on $D$ again turns the four-stranded, once-folded horseshoe into a horseshoe that’s folded over twice and has eight strands. You can imagine how this continues as you perform the operation again and again: you get ever more snaky horseshoes with ever more strands. The simple horseshoe operation leads to quite a bit of complexity when you apply it repeatedly.

Horseshoe dynamics

The operation gives a dynamical system: as you apply the operation repeatedly, points in the region $D$ are moved around $D$ . A point $x_0$ in $D$ is moved by the operation (which we’ll call $f$ ) to another point $x_1$ in the horseshoe, which in turn is moved to a point $x_2$ in the folded horseshoe when you apply $f$ again, and so on. You can continue like this indefinitely to get an infinite sequence $x_0, x_1, x_2, x_3,...$ of points. That sequence is called the forward orbit of $x_0$ .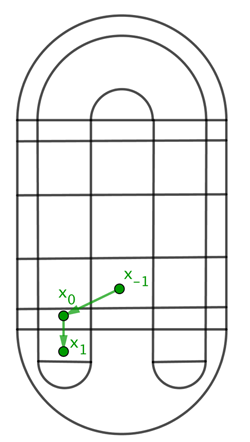

The point x_-1

maps to the point x₀ under f, which in turn maps to x₁.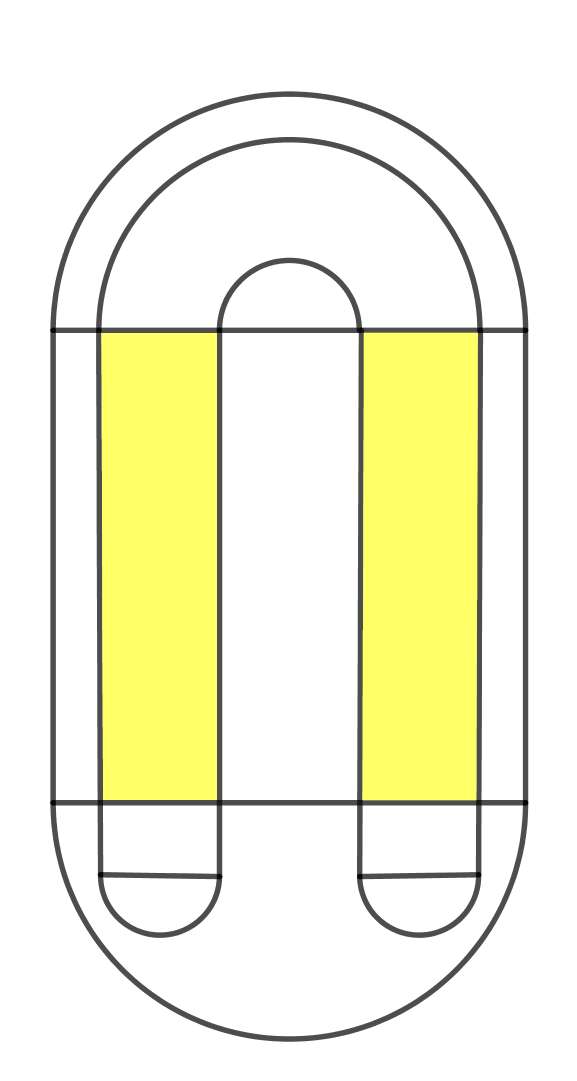

We can also go the other way around. Rather than asking where a point $x_0$ goes to under $f$ you can ask where it comes from. Is there a point in $D$ that goes to $x_0$ when you apply $f$ to it? There may not be such a point, but if there is we call it $x_{-1}$ . Similar we write $x_{-2}$ for the point that goes to $x_{-1}$ under $f$ (if it exists), $x_{-3}$ for the point that goes to $x_{-2}$ under $f$ (if it exists), and so in. The sequence $x_{-1}, x_{-2}, x_{-3},...$ is called the backward orbit of $x_0$ .

All the exciting things happen on the Square $S$ that forms the body of the shape $D$ . If $x_0$ is in $S$ , then there’s no guarantee that $x_1$ is also in $S$ — it could lie in the U-bend above $S$ or in the two ends sticking out from its bottom edge. However, for some points $x_0$ , the point $x_1$ does lie in $S$ : if that’s the case then $x_1$ lies in one of the two vertical strips in which the horseshoe intersects the square $S$ .

If x₀ is in S and x₁ is also in S, then x₁ lies in one of these two vertical strips.

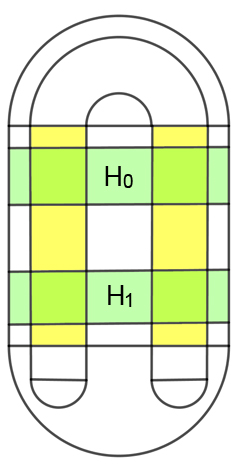
A bit of thought will convince you that $x_0$ must therefore lie in one of two horizontal strips, $H_0$ and $H_1$ . As you apply $f$ to the square, these horizontal strips get squeezed horizontally and stretched vertically, and after the horseshoe has been formed, get put down on our two vertical strips. Points in $S$ that are not within these horizontal strips get mapped to the U-bend, or the two ends sticking out from the bottom edge.

If x₀ is in S and x₁ is also in S, then x₀ lies in one of the two horizontal strips.

What can we say about points $x_0$ whose entire forward and backward orbits lie in $S$ ? You can start drawing pictures of where horseshoes with increasing number of folds go to or come from as you apply $f$ , or $f$ backwards, repeatedly. It’ll give you a headache after a while, but it’s worth it, as the structure you’ll find is very interesting. However, we won’t do this here: there’s a neater way to figure out the dynamics of $f$ on the collection of points whose orbits never leave $S$ .

First, write $L$ for this collection of points whose forward and backward orbits don’t leave $S$ . Given a point $x_0$ in $L$ think of any other point $x_ n$ in the orbit of $x_0$ , where $n$ can be positive or negative. The point $x_{n+1}$ is the next point along the orbit. And since the entire forward and backward orbit of $x_0$ lie in $S$ , we know that $x_ n$ and $x_{n+1}$ both lie in $S$ . By exactly the same reasoning as above, this means that $x_{n+1}$ lies in one of the two vertical strips, which in turn means that $x_ n$ lies in one of the two horizontal strips $H_0$ or $H_1$ . That’s true for any $n$ , in other words, it’s true for every point in the forward and backward orbits of $x_0$ . As you move through the orbits, the points bounce around between $H_0$ and $H_1$ .

Shifty dynamics

This means we can write down a sequence for each $x_0$ in $L$ . First, write down a $0$ if $x_0$ in $H_0$ and a $1$ if $x_0$ in $H_1$ . Now look at $x_1$ and write down a $0$ if $x_1$ in $H_0$ and a $1$ if it’s in $H_1$ . Then look at $x_2$ and write down a $0$ if $x_2$ in $H_0$ and a $1$ if it’s in $H_1$ . And so on. For each point $x_ n$ in the forward orbit of $x_0$ you write down a $0$ or a $1$ . This gives you an infinite sequence of $0$ s and $1$ s.

We can write down a sequence for the backward orbit of $x_0$ in a similar way, only now we write it from right to left. The first entry (on the right) is $0$ if $x_{-1}$ is in $H_0$ and $1$ if $x_{-1}$ is in $H_1$ . The second entry (from the right) is $0$ if $x_{-2}$ is in $H_0$ and $1$ if $x_{-2}$ is in $H_1$ . And so on. This gives a sequence of $0$ s and $1$ s, infinite in the left.

Now glue the two sequences together, with a dot between the sequence to separate them. For example the sequence

$...11111111.111111111...$

denotes the point $p$ whose entire backward and forward orbits lie in $H_1$ .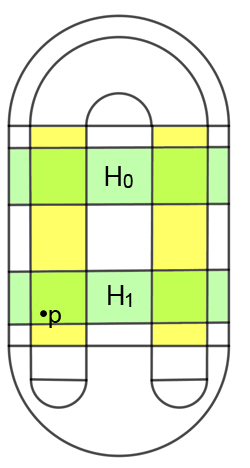

The point p whose sequence consists entirely of 1s.

It turns out that the correspondence between these bi-infinite sequences and points in $S$ whose orbits never leave the square is exact. You can prove that for every point in $L$ there is a unique bi-infinite sequence with a dot, and for every bi-infinite sequence with a dot there is a unique point in $L$ . If two points in $S$ are close to each other, then their corresponding sequences agree to a large number of places to the left and right of the dot, and vice versa — the closer they are, the more places agree. And best of all, applying the map $f$ to a point in $S$ corresponds to shifting the dot in its sequence to the right by one place, and applying $f$ backwards corresponds to shifting it along to the right by one place. This kind of symbolic dynamics is used a lot in the theory of dynamical systems and it often makes things marvellously transparent, as we will see next.

About this article

Marianne Freiberger is editor of Plus. She talked to Stephen Smale at the Heidelberg Laureate forum 2017.

Comments

Hmmm...

Hey now - is someone trying to make a Damascus horseshoe here...?