Solving quadratics in pictures

The area of this larger rectangle is $x^2+px$ which, by our equation, is equal to $q.$ But it turns out that we can rearrange it to very nearly form a square. Simply slice the small rectangle into two strips with sides of lengths $x$ and $p/2$: And move one strip so it aligns with the bottom edge of the square: Let's call this region $R$. It still has area $x^2+px = q.$ But if we add a little square of side length $p/2$ to the bottom right corner of $R$ we get a big square with side length $x+p/2$ and area $\left(x+p/2\right)^2.$ Therefore, $$ \mbox{Area of the big square} = \left(x+p/2\right)^2 = \mbox{Area of R}+ \left(p/2\right)^2 = q + \left(p/2\right)^2.$$ Taking the square root of both sides gives $$x+p/2 = \pm{\sqrt{q + p^2/4}}.$$ Subtracting $p/2$ from both sides gives \begin{equation}x = \pm{\sqrt{q + p^2/4}}-p/2.\end{equation} How is that related to the quadratic formula we learn about at school? We usually write a general quadratic equation as $$ax^2+bx+c=0.$$ Dividing through by $a$ so that the coefficient of $x^2$ is 1 gives $$x^2 + \frac{b}{a}x + \frac{c}{a} = 0.$$ Bringing $\frac{c}{a}$ over to the other side gives $$x^2 + \frac{b}{a}x = -\frac{c}{a}.$$ So comparing with our equation above we see $p=\frac{b}{a}$ and $q=-\frac{c}{a}.$ Substituting these for $p$ and $q$ in expression (1) recovers the general quadratic formula $$x = \frac{-b\pm{\sqrt{b^2-4ac}}}{2a}.$$

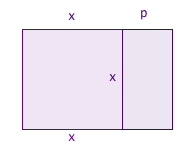
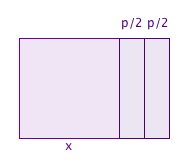
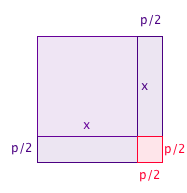
To say that the Babylonians knew this formula is a little misleading. Firstly, they didn't know about negative numbers, so they could only solve quadratics that had a positive solution. Also, they didn't write their maths using symbols and letters as we do, but using words. So a Babylonian student might be given questions such as:

If I add to the area of a square twice its side, I get 48. What is the side?

Which, writing $x$ for the side, translates to the equation $$x^2+2x=48.$$ The Babylonians knew about sequences of steps they could perform to find the solution to such a question — which is why we say they knew about the quadratic formula.