Is space like a chessboard?

Physicists at the University of California, Los Angeles (UCLA) set out to design a better transistor and ended up with a discovery which suggests a new explanation of electron spin and may even lead to a new understanding of the nature of space.

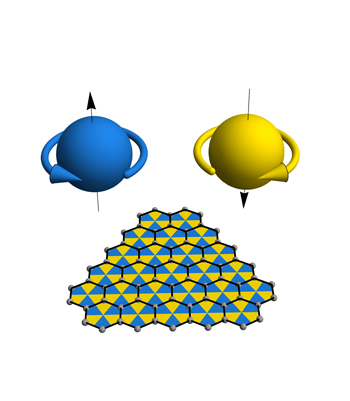
An electron in graphene hops from carbon atom to carbon atom as if moving on a chessboard with triangular tiles. At low energies the individual tiles are unresolved, but the electron acquires an internal spin quantum number which reflects whether it is on the blue or the gold tiles. Thus the electron's spin could arise not from rotational motion of its substructure, but rather from the discrete, chessboard-like structure of space. (Image: Chris Regan/CNSI)

Space is usually considered infinitely divisible — given any two positions, there is always a position halfway between. But in a recent study aimed at developing ultra-fast transistors using a new material called graphene, researchers from the UCLA Department of Physics and Astronomy and the California NanoSystems Institute show that dividing space into discrete locations, like a chessboard, may explain how point-like electrons, which have no finite radius, manage to carry their intrinsic angular momentum, or spin.

While studying graphene's electronic properties, professor Chris Regan and graduate student Matthew Mecklenburg found that a particle can acquire spin by living in a space with two types of positions — dark tiles and light tiles. The particle seems to spin if the tiles are so close together that their separation cannot be detected. "An electron's spin might arise because space at very small distances is not smooth, but rather segmented, like a chessboard," Regan said. Their findings are published in the March 18 edition of the journal Physical Review Letters.

In quantum mechanics, spin up and spin down refer to the two types of states that can be assigned to an electron. That the electron's spin can have only two values — not one, three or an infinite number — helps explain the stability of matter, the nature of the chemical bond and many other fundamental phenomena.

However, it is not clear how the electron manages the rotational motion implied by its spin. If the electron had a radius, the implied surface would have to be moving faster than the speed of light, violating the theory of relativity. And experiments show that the electron does not have a radius; it is thought to be a pure point particle with no surface or substructure that could possibly spin.

In 1928, British physicist Paul Dirac showed that the spin of the electron is intimately related to the structure of spacetime. His elegant argument combined quantum mechanics with special relativity, Einstein's theory of spacetime.

Dirac's equation, far from merely accommodating spin, actually demands it. But while showing that relativistic quantum mechanics requires spin, the equation does not give a mechanical picture explaining how a point particle manages to carry angular momentum, nor why this spin is two-valued.

Unveiling a concept that is at once novel and deceptively simple, Regan and Mecklenburg found that electrons' two-valued spin can arise from having two types of tiles — light and dark — in a chessboard-like space. And they developed this quantum mechanical model while working on the surprisingly practical problem of how to make better transistors out of a new material called graphene.

Graphene, a single sheet of graphite, is an atomically-thin layer of carbon atoms arranged in a honeycomb structure. First isolated in 2004 by Andre Geim and Kostya Novoselov, graphene has a wealth of extraordinary electronic properties, such as high electron mobility and current capacity. In fact, these properties hold such promise for revolutionary advances that Geim and Novoselov were awarded the 2010 Nobel Prize a mere six years after their achievement.

Regan and Mecklenburg are part of a UCLA effort to develop extremely fast transistors using this new material. "We wanted to calculate the amplification of a graphene transistor," Mecklenburg said. "Our collaboration was building them and needed to know how well they were going to work." This calculation involved understanding how light interacts with the electrons in graphene.

The electrons in graphene move by hopping from carbon atom to carbon atom, as if hopping on a chessboard. The graphene chessboard tiles are triangular, with the dark tiles pointing "up" and light ones pointing "down." When an electron in graphene absorbs a photon, it hops from light tiles to dark ones. Mecklenburg and Regan showed that this transition is equivalent to flipping a spin from up to down.

In other words, confining the electrons in graphene to specific, discrete positions in space gives them spin. This spin, which derives from the special geometry of graphene's honeycomb lattice, is in addition to and distinct from the usual spin carried by the electron. In graphene the additional spin reflects the unresolved chessboard-like structure to the space that the electron occupies.

"My adviser [Regan] spent his Ph.D. studying the structure of the electron," Mecklenburg said. "So he was very excited to see that spin can emerge from a lattice. It makes you wonder if the usual electron spin could be generated in the same way."

"It's not yet clear if this work will be more useful in particle or condensed matter physics," Regan said, "but it would be odd if graphene's honeycomb structure was the only lattice capable of generating spin."

Jennifer Marcus works for the UCLA newsroom.

Further reading

• Find out more about graphene in the Plus article And the Nobel Prize in Mathematics goes to...
• Find out more about electron spin in the Plus article In a spin
• Find out more about the structure of space at the smallest level in the Plus article Quantum geometry.