Stanley Osher

"You open a door and strange things come from new directions. It's overwhelming, like being drunk." This is how Stanley Osher, winner of the Gauss Prize at the International Congress of Mathematicians 2014, describes his lifelong pursuit of interesting mathematical challenges outside of mathematics. His curiosity about other areas of science, his ability to learn their languages and his insatiable appetite to make algorithms better have resulted in a revolutionary impact in areas including medical imaging, sonic booms, movie animation and microchip design and manufacture.

It was the movement of flames that Osher and his colleage James Sethian were interested in describing in the 1980s. Flames are tricky to describe mathematically as they split and merge as they burn. Think of a fire lit in a field of dry grass. As it burns it creates a ring of fire that moves outward, growing in size. Traditionally you'd describe this changing shape by picking points on the burning edges, keeping track of their positions and how they are connected, and then describing how these points move. But what if two fires are burning and their edges cross over – the two fires coalescing into one – or if a single fire front splits into two? Then this edge-point description quickly become very complicated as you have to remove points from or add points to your description and keep track of which are now connected along the burning edges.

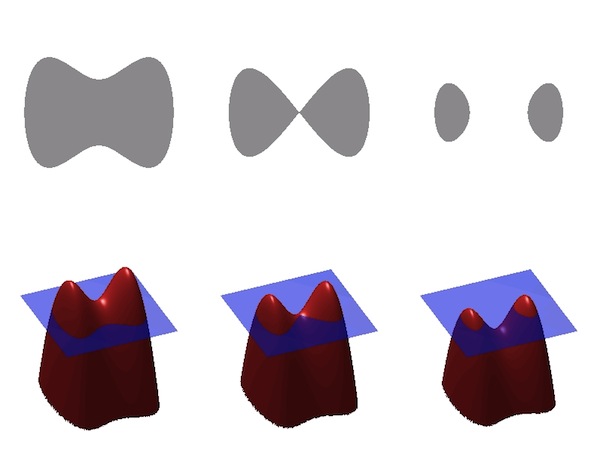
You can think of a changing two-dimensional shape as a slice moving through an unchanging three-dimensional shape.

Instead Osher and Sethian imagined the burning edges as a slice through a three dimensional surface: the changing shape of these edges corresponded to moving the slice through the three dimensional surface. Think of a mountain range with two peaks. A slice near the top of this surface gives you two separate closed edges, one for each peak. But as you move the slice down the mountain range and pass through the valley, the separate edges in the slice merge together.

This method of describing how shapes change by imagining them as a slice through a higher-dimensional surface is called the level set method. Our example was describing how a shape in a two dimensional plane changes (the burning edges of the fires in a field) by thinking of it as a slice moving though an unchanging surface in three dimensions. You can extend this mathematics to higher dimensions, for example describing how a shape changes in three dimensions (such as the dancing shapes of the flames themselves) by thinking of them as a slice moving through a four-dimensional object.

"We didn't know the level set method would take the universe by storm," says Osher. It is now a fundamental technique in a wide range of areas, including Hollywood. It is used by almost every movie studio in the animation of complex shapes such as water, flames and snow. Osher's past student Ron Fedkiw, now a professor of computer science as UCLA, won an Academy Award in 2007 for his work developing film animation software using these methods.

A sonic boom (Image from NASA)

One of the most astonishing things about Osher is how he has translated work and concepts in one area into another. He estimates that he spends at least half his time working with scientists from outside of mathematics: "It's good to get out there and listen to what they have to say. There might be a language barrier but you have to be friendly and learn the language."

Such a collaboration came about with Leonid Rudin, a computer scientist who had realised that the discontinuities in shockwaves, such as the sonic boom caused by the instantaneous change in pressure at the nose of a supersonic jet, is a similar problem to automatically detecting the edges in images. After a discussion they realised the maths Osher and colleagues had developed to deal with the discontinuities in the airflow around jets (called shock capture) could be applied to image analysis. (You can read more about the maths behind sonic booms here.)

This has revolutionised image analysis leading to improvements in medical imaging both in reducing the time these scans take and in the accuracy of the image. Osher and Rudin's company built on these techniques, Cognitech produces software and training is now widely used by police for forensic image analysis. Famously the company helped to identify perpetrators of a vicious attack on a truck driver from blurry police footage from the LA riots in 1992.

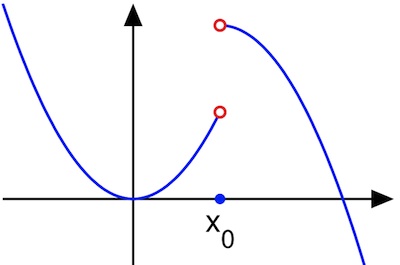
A discontinuous function

Much of Osher's work comes from dealing with discontinuities. Discontinuities are where life gets interesting – whether the abrupt change in colour defining the outlines of features in an MRI scan, the instantaneous drop in air pressure at the nose of a supersonic jet or the edges of the dancing flames in your fireplace.

But discontinuities are hard to handle mathematically. Imagine you have a function (such as the one on the right) with a sharp discontinuity – a point at which the the function jumps. A typical approach to describing a complicated function is to approximate it using well understood smooth functions. But if you use these techniques to describe what is going on near a discontinuity you will either smooth the discontinuity out, so missing out that important information, or you will introduce new spurious values.

"The level set method is different," says Osher. It allows a discontinuity – such as the point where a shape merges or splits – to be described by a higher-dimensional object that is not discontinuous. Rather than having to keep track of all the different pieces separately and how they join or split, you instead have one function, describing the higher dimensional surface, that tracks all of the pieces at the same time. "By adding an extra dimensions you get rid of all the emotional involvement."

Osher is still busy learning new languages and seeing where he can make techniques better. He's currently learning about quantum mechanics to see how these ideas can be applied to material physics. He is also actively involved in improving the accuracy of medical scans of brain and heart signals. "These are very different applications but use very similar mathematics."

The universal nature of mathematics and its resulting power is what have motivated Osher's mathematical career. "We all love maths, the unreasonable effectiveness of maths – it does everything," says Osher. "I like to prove theoreams and all that stuff but I'm more interested in getting something that works. It makes it even more fun when the maths becomes useful."