There are many strange things about quantum mechanics, but perhaps the strangest is that it appears to allow us to edit the past. To understand how this might be possible, we first need to know about the double slit experiment. For this, a brief summary is given below, and a more detailed account is given here.

The double slit experiment

The double slit experiment, first performed in 1801 by the physicist Thomas Young, appeared to provide an unequivocal demonstration that light behaves like a wave. But the importance of the double slit experiment extends far beyond that demonstration because, as Richard Feynman said in 1966:

"In reality, it contains the only mystery ... In telling you how it works, we will have told you about the basic peculiarities of all quantum mechanics."

In Young's experiment the experimental apparatus consists of a barrier with two vertical slits and a screen, as shown in Figure 1 below. Light emanating from each slit interferes with light from the other slit to produce an interference pattern on the screen. This seems to prove conclusively that light consists of waves.

Figure 1: The double-slit experiment. Waves travel from the source (top) until they reach a single slit. A semi-circular wave emanates from the slit until it reaches a barrier, which contains two slits. The two semi-circular waves emanating from these slits interfere with each other, producing peaks and troughs along radial lines that form an interference pattern on a screen (bottom).

However, with modern equipment, we can also see that the interference pattern consists of individual dots, each of which corresponds to a single particle of light, called a photon. This, in essence, the famous wave-particle duality.

Remarkably, even when the light is made so dim that only one photon at a time reaches the screen, the same type of interference pattern builds up over time, as shown in Figure 2. With such a low photon rate, it can take several weeks for the interference pattern to emerge. However, the very fact that an interference pattern emerges at all implies that even a single photon behaves like a wave. This, in turn, seems to imply that each photon passes through both slits at the same time, which is clearly nonsense.

Figure 2: Emergence (a to d) of an interference pattern in a double slit experiment, where each dot represents a photon. Image: Dr. Tonomura and Belsazar, CC BY-SA 3.0.

This raises the question: did the photon really pass through only one slit, and if so, which one?

Did the photon pass through one slit or two?

Before we answer this question, let's think about what we'd see if there was no interference. Imagine we closed one slit, and left the other open, so the photons from that slit are allowed to form a pattern on the screen. Next, only the other slit is left open, and the photons from that slit are allowed to add to their pattern to the screen. Using this procedure, the image captured by the photographic plate is the sum of photons from each slit, with the guarantee that photons from the two slits could not possibly have interfered with each other. The result is a diffraction envelope as shown in Figure 3.

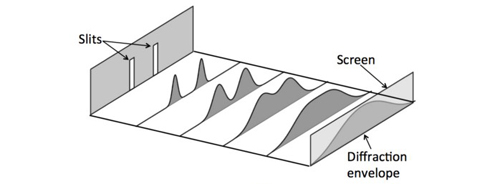
Figure 3: Measuring position at the slits (slit identity) results in a broad diffraction envelope. Here, the height of the curve indicates light intensity.

Now, to attempt to answer the question of whether the photons passed through one or both slits, we could place a photodetector at each slit to find out which slit each photon passed through. However, for reasons that will become clear later, we will consider a different setup. Imagine replacing the screen with an array of long tubes, each of which points at just one slit, as shown in Figure 4. At the end of each tube is a photodetector, such that any photon it detects could have come from only one slit. Note that there should be a pair of detectors at every screen position, with each member of the pair pointing at a different slit. Thus, irrespective of where a photon lands on the screen, the slit from which it originated is measured.

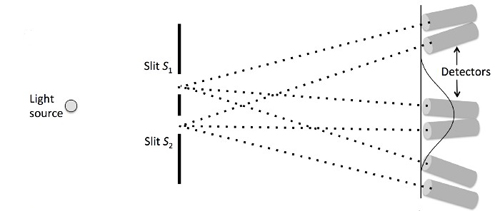
Figure 4: An imaginary experiment for demonstrating wave–particle duality.

If we were to use this imaginary apparatus then we would find that the interference pattern is replaced by the diffraction envelope described above, and as shown in Figure 3. Thus, using detectors to measure which slit each photon passed through (its slit identity) prevents any wave-like behaviour, just as if each photon had travelled in complete isolation as a single particle. If both slits are left open (and no photodetectors are used) then the original interference pattern is restored, as if the individual photons behave like waves (see Figure 5). This wave–particle duality seems to suggest that the way the experiment is measured has a mysterious impact on its outcome.

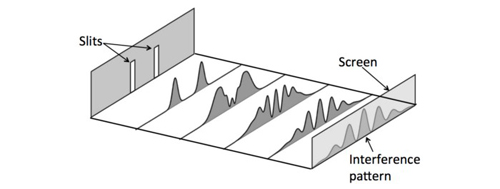
Figure 5: When both slits are left open an interference pattern appears. Here, the height of the curve indicates light intensity.

Heisenberg's uncertainty principle

As counter-intuitive as the result above seems, it is consistent with the most famous principle of quantum physics: Heisenberg's uncertainty principle. It states that it is not possible, in principle, to know with absolute certainty both the position and momentum of a particle – the more accurately the position is known, the less accurately momentum can be known, and vice versa (find out more here). This is not because the measuring instruments are imperfect, but because the notions of position and momentum are inherently fuzzy in the quantum world.

Heisenberg's uncertainty principle relies on the fact that, because both light and matter behave like waves, they can be analysed using Fourier analysis (the main mathematical tool for dealing with waves). This is important because Fourier analysis was used by Heisenberg to derive a mathematical theorem, Heisenberg's inequality (as it is now known), which underpins Heisenberg's uncertainty principle.

In the double slit experiment, the slit identity of a photon can be treated as its position at the barrier. Because the momentum of a particle specifies its direction of travel, the particle's final position on the screen is also specified by its momentum (see Figure 6a). Thus, Heisenberg's uncertainty principle, which is usually stated in terms of position and momentum, guarantees that reducing the uncertainty in slit identity (position) must increase uncertainty in screen position (momentum). So position-momentum uncertainty translates to slit identity-screen position uncertainty in the double slit experiment.

Wheeler's delayed-choice experiment

So far, we have chosen to measure two different aspects of each photon: first, measuring each photon's screen position (which translates into momentum at a slit); and second, using tube detectors to measure slit identity (which translates into position at the barrier).

Measuring photon screen position accurately means that the complementary measurement, slit identity, is uncertain. Because the experimental does not change in the time taken for the photon to travel from the barrier to the screen, this uncertainty makes it seem plausible (or at least acceptable) that each photon could have passed through both slits. Similarly, measuring slit identity accurately, it seems plausible that each photon passes through only one slit.

But there is an alternative experiment, which involves changing the experimental setup while each photon is in transit between the slits and the screen. If the decision about what is measured alters how each photon behaves then it seems reasonable that this decision must be made before each photon starts its journey from the barrier to the screen. However, what if the decision on whether to measure screen position or slit identity is made after each photon has passed through the slit(s), but before it has reached the screen or tube detectors? This is Wheeler's delayed-choice experiment, named after the physicist John Wheeler, and depicted in Figure 6 below.

Such an experiment is conceptually easy to set up. Once a photon is in transit between the slits and the screen, we can decide whether to measure the photon's screen position (by leaving the screen in place, Figure 6b), or slit identity (by removing the screen so that the tube detectors can function, Figure 6a).

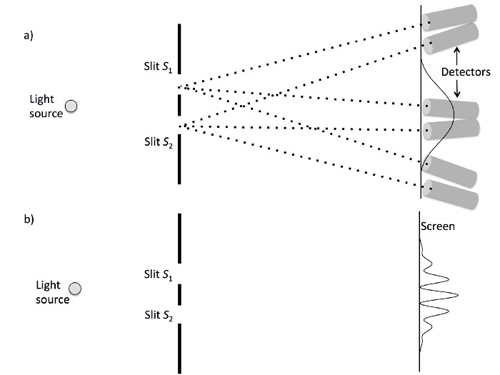
Figure 6: An imaginary experiment for demonstrating wave–particle duality. a) If slit identity (photon position at the barrier) is measured using an array of oriented detectors at the screen then momentum (direction) precision is reduced, and a diffraction envelope is observed on the screen, as in Figure 3. b) If slit identity is not measured then the location at which a photon hits the screen effectively measures its direction (photon momentum) with high precision, then an interference pattern is observed. In Wheeler's delayed-choice experiment, the decision to measure either a) slit identity, or b) photon momentum is made after the photon has passed through the slit(s).

In 2007 the physicist Vincent Jacques and his colleagues, published the results of an experiment which is conceptually no different from the experiment described above, using measurement devices called interferometers. Translating from the Jacques interferometer experiment, the photons' screen positions are effectively measured by leaving the screen in place, yielding an interference pattern on the screen. This fits with the account above: accurate measurement of screen position corresponds to each photon passing through both slits, which is consistent with wave-like behaviour. In contrast, when the screen is removed, an array of detectors is revealed that detects each photon's slit identity, and the resultant diffraction envelope formed is consistent with photons behaving like particles.

Crucially, the decision to measure screen position (by leaving the screen in place) or slit identity (by removing the screen) was made (at random, and by a physical random number generator) after each photon had passed through the slit(s); so the behaviour of each photon as it passed through the slit(s) depended on a decision made after that photon had passed through the slit(s). In essence, it is as if a decision made now about whether to measure slit identity or screen position of a photon (that is already in transit from the slits to the screen) retrospectively affects whether that photon passed through just one slit or both slits.

In principle, the slit–screen distance can be made so large that it takes billions of years for each photon to travel from the slit(s) to the screen. In this case, a decision made now about whether to measure the slit identity or screen position of a photon seems to retrospectively affect whether that photon passed through just one slit or both slits billions of years ago.

As we should expect, these results are consistent with Heisenberg's uncertainty principle. Regardless of when the decision is made, if the detectors measure slit identity then this must increase uncertainty regarding the photon's screen position, which causes the interference pattern to be replaced by a simple diffraction pattern. It is a mystery how any physical mechanism could trade uncertainty in slit identity for uncertainty in screen position, and it is even more of a mystery how this trade could work backwards across time. However, the fact remains that if such a mechanism did not exist then Heisenberg's uncertainty principle would be violated.

Editing the past

So, suppose we wanted to edit the past. First, how could we do so, and second, how far back in time could that edit be?

Well, to answer the first question (and as described above), a decision made now about whether or not to leave the screen in place seems to determine how photons behaved in the past. Specifically, if we wish to ensure that each photon passed through just one slit then we should remove the screen (allowing the detectors to measure which slit each photon exited). Conversely, if we wish to ensure that photons passed through both slits then we should leave the screen in place. In both cases, this decision can be made after the photons have passed through the slit(s).

Second, the temporal range of our edit depends on how long the photons have been in transit from the double slits to the screen/detectors. This looks as if we need to have a double slit experiment that has been set up in the distant past. However, there are natural phenomena, like gravitational lensing, which can be used to effectively mimic the double slit experiment; as if slits are so far away that the photons we measure have been in transit for many years. Thus, in principle, temporal editing can reach back to the big bang, some 14 billion years ago.

Finally, it should be noted that not everyone (including Wheeler) agrees that Wheeler's delayed choice experiment edits the past. Like most of quantum mechanics, the equations that define the results of the delayed choice experiment do not have a single unambiguous physical interpretation. Indeed, the difficulty of interpretation can only be fully appreciated by understanding the equations that govern quantum mechanics. Fortunately, those equations are usually more daunting than the underlying physics they seek to describe.

Further reading

This article is based on an extract from the book The Quantum Menagerie by James V Stone (published December 2020). You can see Chapter 1, the table of contents, and book reviews here.

You can also find out more about quantum mechanics in our package Who killed Schrödinger's cat?

About the author

James V Stone is an Honorary Associate Professor at the University of Sheffield, UK.