
Why are sunsets red?
The city of Santa Fe, NM, USA, lies at the foot of the southernmost range of the Rocky Mountains. It was founded in 1610 by the Spanish conquistadores as the capital of their northern territories in the Americas. They named the nearby mountain range the Sangre de Cristo mountains, meaning "blood of Christ". This name was inspired by the deep red glow that is cast over these mountains just before the Sun disappears below the horizon at the end of the day. But what is it that causes everything to turn red during a sunset?

Last sunlight on the Sangre de Cristo mountains, New Mexico, USA. Image: Wim Hordijk.
Light is a mysterious phenomenon that seems to have a split personality. Sometimes it acts like waves and sometimes like particles. This two-faced phenomenon is known as the wave-particle duality. To understand why sunsets are red (or at least red-ish), we need to consider the wave-like behaviour of light.
Waves
In mathematics, a wave represents a regular oscillating motion over time, going from a high point to a low point and back, just like waves in the ocean. The figure below shows an ideal (mathematical) wave. There are two main properties that define the particular shape of a wave: its wavelength and its amplitude.
A wave's wavelength is the distance between two consecutive high points ("peaks"), or equivalently, the distance between two consecutive low points. A wave's amplitude is the height of its peaks. Both of these properties are also illustrated in the figure.
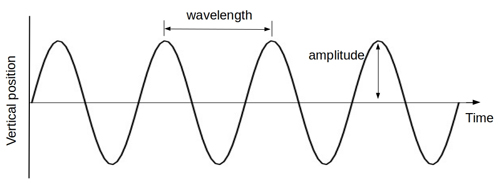
Figure: Wim Hordijk.
Mathematically, such a wave can be described by a sine function (sin):
$$y=A\sin{(wt)}.$$ The variable $t$ is time (the horizontal axis in the figure), and the variable $y$ is the vertical position (vertical axis) at any given time $t$. The parameter $A$ determines the wave's amplitude, and the parameter $w$ its frequency, i.e., the number of wave peaks per unit of time. The frequency of a wave is inversely proportional to its wavelength. If you double the wave's frequency (by making $w$ twice as large), its wavelength will halve.Sound and light as waves
One very familiar form of waves are sound waves that travel from your stereo speakers through the air to your ears. You hear sound waves with very large wavelengths (low frequencies) as very low notes (e.g., from a bass), and sound waves with very small wavelengths (high frequencies) as very high notes (e.g., from a violin).
In fact, there is a direct mathematical relationship between the wavelength (frequency) of a sound wave and the note you hear. The sound wave corresponding to middle C on a piano has a frequency of about 262Hz, meaning 262 peaks per second. The C one octave higher has double that frequency (524Hz), and the C one octave lower has half that frequency (131Hz).
The speed of sound in air at room temperature is about $c=343$ meters per second. You can convert the frequency $w$ of a sound wave to its corresponding wavelength by simply dividing this speed $c$ by the wave's frequency $w$. For example, the wavelength for middle C is $343/262 = 1.31$ meter.Finally, a sound wave's amplitude determines the sound's loudness. A low amplitude will result in a very soft sound, while a high amplitude results in a very loud sound.

Sunset in Lausanne, Switzerland. Image: Wim Hordijk.
When it comes to sunsets, light can also be considered a wave, just like sound. Therefore, light and sound have many things in common. For example, just like the wavelength of a sound wave determines which note you hear, the wavelength of a light wave determines which colour you see.
Now here is another mysterious thing about light. White light, such as that coming from the Sun, contains all wavelengths! This can be seen by shining a ray of sunlight through a prism, as beautifully illustrated in the image below. The glass of the prism, being of a different density than the air, causes the light ray to bend.
However, different wavelengths bend at different angles. For example, shorter wavelengths (around 400nm, which you see as blue and purple) bend more strongly than longer wavelengths (around 700nm, which you see as orange and red). This is why the original white ray of sunlight turns into a beautiful rainbow of colour. (To find out what gives rise to the rainbows we see in the sky see this article).
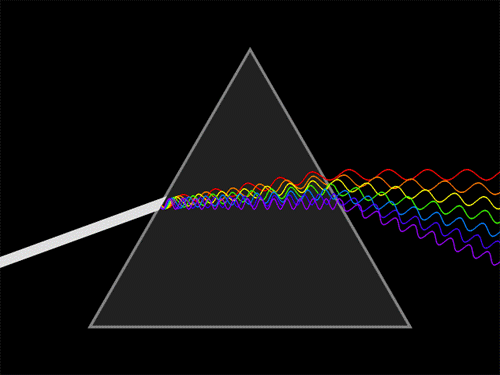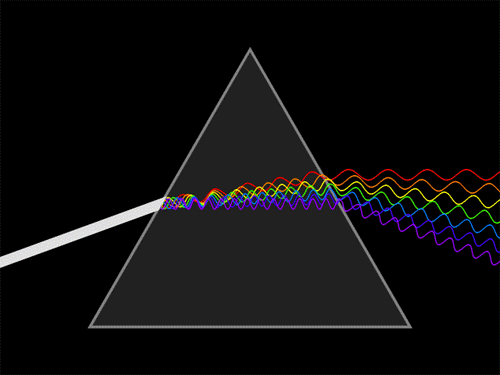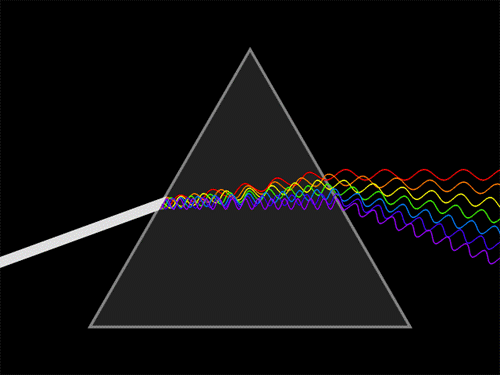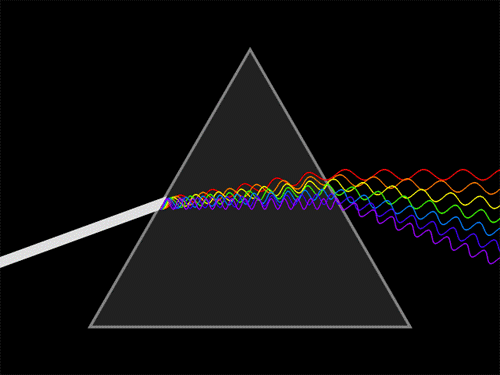
A prism bends light waves with different wavelengths at different angles. Image Lucas V. Barbosa.
Light scattering
When sunlight enters the Earth's atmosphere, it bumps into all kinds of molecules, particles, and water droplets along the way. This causes some of the light to scatter, and thus not all sunlight reaches the Earth's surface. However, just like different wavelengths are bent differently by a prism, they are also scattered differently by the Earth's atmosphere. In fact, as with the prism, shorter wavelengths are scattered more strongly than longer wavelengths.
In the middle of the day, when the Sun is directly above your head, the amount of atmosphere that the sunlight has to travel through to reach you is relatively small (see image below). Thus the overall amount of scattering is also relatively small. However, at sunrise or sunset, the light has to travel through a much larger portion of the atmosphere (as illustrated below). Therefore, the total amount of scattering is also larger.
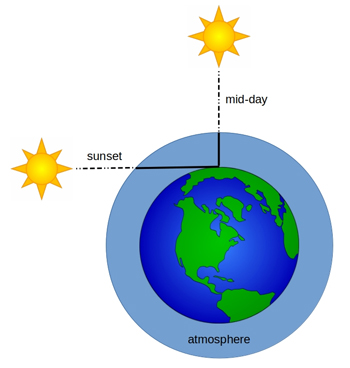
Figure: Wim Hordijk.
When the total amount of scattering is relatively small (i.e., during the day), the different scattering of shorter and longer wavelengths is hardly noticeable, as enough light of each wavelength will still reach you. However, close to sunset this difference does become noticeable.
Shorter wavelengths (blue and purple) are scattered significantly more strongly than longer wavelengths (orange and red) on their long path through the atmosphere. As a consequence, significantly more of the orange-red side of the light spectrum reaches you than of the blue-purple side.
And this is exactly why everything looks orangy-red during sunsets...

Sunset in the Kaikoura mountains, New Zealand. Image: Wim Hordijk.
About the author

Wim Hordijk is an independent and interdisciplinary scientist and popular science writer. He has worked on many research and computing projects all over the world, mostly focusing on questions related to evolution and the origin of life. More information about his research can be found on his website.