
Outer space: Pylon of the month

There are some fascinating websites about, but none more beguiling than the iconic Pylon of the Month site, once devoted to providing monthly pin-ups of the world’s most exciting and seductive electricity pylons. Alas, Pylon of the Month now seems to have become a cobweb site, but there is still something to learn from it, since for the mathematician every pylon tells a story. It is about something so prominent and ubiquitous that, like gravity, it goes almost unnoticed.
Next time you go on a train journey look carefully at the pylons as they pass swiftly by. Each is made of a network of metal struts that make use of a single recurring polygonal shape. That shape is the triangle. There are big triangles and smaller ones nested within them. Even apparent squares and rectangles are merely separate pairs of triangles. The reason forms a small part of an interesting mathematical story that began in the early nineteenth century with the work of the French mathematician Augustin-Louis Cauchy. Of all the polygonal shapes that we could make out of straight struts of metal, the triangle is special. It is the only one that is rigid.
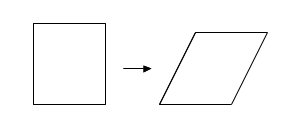
Turning a rectangle into a parallelogram.
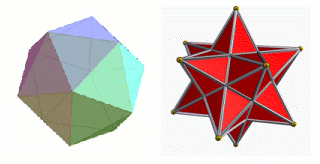
The icosahedron on the left is a twenty-sided convex polyhedron. The small stellated dodecahedron on the right is not convex because some of its faces point inwards. Both polyhedra are rigid. The image on the right was created with Robert Webb's Great Stella software.
If we move on to three-dimensional shapes then the situation is quite different: Cauchy showed that every convex (so the faces all point outwards) polyhedron with rigid faces, and hinged along its edges, is rigid. And, in fact, the same is true for convex polyhedra in spaces with four or more dimensions as well.
What about the non-convex polyhedra, where some the faces can point inwards? Here, the question remained open until 1978 when Robert Connelly, now at Cornell University, found an example with non-convex faces that is not rigid, and then showed that in all the non-rigid cases the total volume remains the same during the shifts.
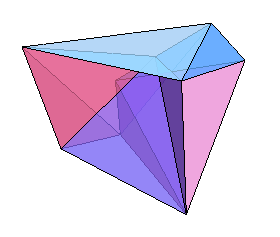
Steffen's flexible polyhedron has 14 triangular faces, 21 edges and 9 vertices. This image is taken from the Wolfram Demonstrations Project, which enables you to download a demonstration of the polyhedron flexing.
Update May 2009: Good news! Pylon of the Month lives again! Plus reader Kevin Mosedale contacted us with news that he has set up a successor site, www.pylonofthemonth.org.