Secrets from a bathroom floor

September 2009

Tilings have adorned buildings from ancient Rome to the Islamic world, from Victorian England to colonial Mexico. In general, the word tiling refers to any pattern that covers a flat surface, like a painting on a canvas, using non-overlapping repetitions of one or more shapes, so that the design does not leave any empty spaces. Contemporary tilings can be found in African-American quilts, Indonesian batiks, molas from the San Blas de Cuna Islands, and Aboriginal paintings.

Tiling was a favorite means of expression for the Dutch artist M. C. Escher (1898-1972), who repeatedly expressed his love for this art form, acknowledging at the same time the influence on his work of the mosaics he admired and sketched from Moorish buildings in Southern Spain. In spite of this influence, Escher's art went far beyond anything seen before. He produced enigmatic tilings, with strange creatures and mutating landscapes that suggest a craft free from any worldly limitation. This perception however, owned to Escher's mastery, is far from true. Tiling is a very precise art, where not much can be left to chance. Even the simplest tilings fall to the spell of mathematical principles. We can push and turn and wriggle, but if the maths is not right, it isn't going to tile.

Not all tiles are created equal

To see how mathematics can limit the fancy of the best tile installer, we first try our hand at tiling with copies of just one regular polygon, that is to say a shape having sides of the same length and equal angles. One of these regular polygons, a square, is shown in figure 1(a), while figures 1(b) and 1(c) show polygons that are not regular. In figure 1(b) not all the angles are equal, and in figure 1(c) not all the sides have the same length.

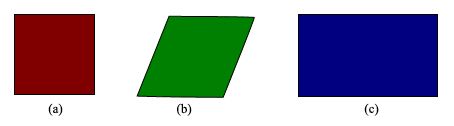
Figure 1: Regular and non-regular polygons.

Not only do we want to use copies of just one regular polygon, but we also want to place them vertex to vertex, that is to say, with the vertices of one copy touching only the vertices of other copies. These tilings are called regular. For instance, in figure 2, tilings (a), (b) and (c) are regular, while tilings (d), (e) and (f) are not: the squares in tiling (d) lie in a sliding mood, while tilings (e) and (f) use more than one kind of regular polygon each, regular octagons and squares for (e), regular hexagons and equilateral triangles for (f).

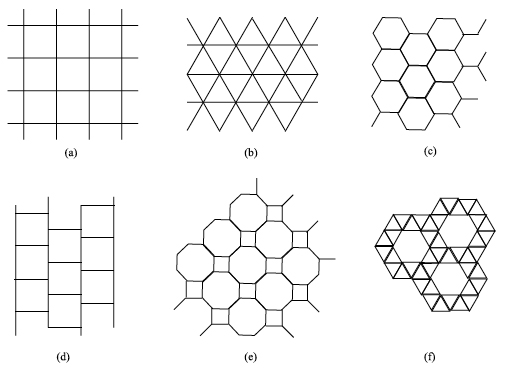
Figure 2: Regular and non-regular tilings.

As the tilings (a), (b) and (c) in figure 2 show, squares, equilateral triangles and regular hexagons do make up regular tilings, a fact that was known to Pythagoras' followers in the fifth century BC. But Mother Mathematics says that no other regular polygon can claim the same. Why? If we look at the regular tilings in figure 2, we see that the angles meeting at each vertex add up exactly to a complete revolution, or 360°. What happens with, say, regular octagons?

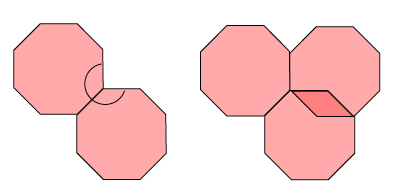
Figure 3: Not all tiles are created equal.

As figure 3 illustrates, two regular octagons fall short of a complete revolution, while three regular octagons produce some overlapping. Tiling (e) in figure 2 shows that the perfect tiling companion of two regular octagons is a smaller square wedged between them.

So, our claim about which regular polygons can tile a plane regularly is really a claim about the size of their angles. To say that a regular polygon will produce a regular tiling of a plane is the same as saying that the size of its angle divides exactly into 360°. It is easy to check that this is true for the regular tilings in figure 2: the square, triangle and hexagon have internal angles of 90°, 60° and 120° and each of these numbers divides 360°.

Now, if we want to show that only equilateral triangles, squares and regular hexagons make up regular tilings, we need to show that the angle of any other regular polygon will not divide exactly into 360°. We can do this using a mix of geometry and algebra. Figure 4(a) shows a regular polygon with $n$ sides and angle $\alpha$ . The generic number of sides $n$ can be 3, 4, 5, and so on. We haven't completed the picture of our polygon because we do not want to fall into thinking about a particular polygon. In figure 4(b) we have highlighted one of the $n$ isosceles triangles that compose our polygon.

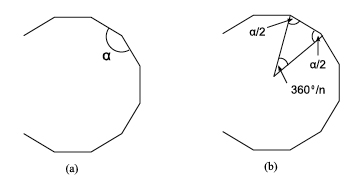
Figure 4: Size of an inner angle.

A little thought shows that the angles of the triangle must be equal to $\frac{\alpha }{2}$ , $\frac{\alpha }{2}$ , and $\frac{360}{n}$ , as the figure suggests. We also know that the sum of these three angles has to be $180^{\circ }$ . Or, in symbols,

$\frac{\alpha }{2} + \frac{\alpha }{2} + \frac{360}{n} = 180,$

$\alpha = 180 - \frac{360}{n}.$

Now we are looking for those regular polygons for which the ratio $\frac{360}{\alpha }$ is a whole number. If we substitute this condition in our newly acquired formula for $\alpha$ , we see that we are looking for those values of $n$ for which $180-\frac{360}{n}$ divides exactly into 360. In other words,

$\frac{360}{180-\frac{360}{n}} = \frac{1}{\frac{1}{2} - \frac{1}{n}}=\frac{2n}{n-2}$

must be equal to a whole number.

At this point, our geometric problem of tiling has become the following algebra problem: To show that $2n$ is divisible by $n-2$ only when $n = 3, 4, 6.$ By division, we can write

$\frac{2n}{n-2}= 2 +\frac{4}{n-2}.$

Now the only way $\frac{4}{n-2}$ can be a number greater or equal to 1 is when $n\leq 6$ , and it is easy to see that $n=5$ is not a possibility. So we are done. We now know for sure that the only regular tilings of the plane using one regular polygon are the first three tilings depicted in figure 2.

Sliding the tile

It has been said that mathematicians do not know where to stop, meaning that we always find yet another wrinkle to explore. Here is our new wrinkle: Tiling (d) in figure 2 shows that we can build a sliding tiling using copies of a square. Is this true for an equilateral triangle? How about a regular hexagon? How about other regular polygons?

Let us consider first the case of equilateral triangles. We can start with two equilateral triangles sitting as in figure 5(a).

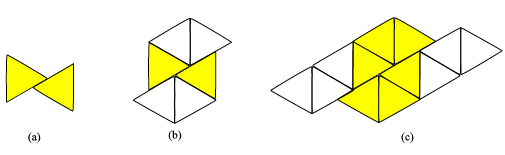
Figure 5: Sliding the tile.

Since 3 × 60° = 180°, we should be able to exactly fit another four copies of the triangle, two above and two below, as shown in figure 5(b). The result is a regular hexagon broken into two halves, with one half slid along the other. Now we can see what is going on: if we break the regular tiling (b) in figure 2 along all or some of the horizontal lines, or along all or some of the slanted lines, and if we slide the strips along the fracture lines, we obtain a tiling, like the one shown in figure 5(c).

We could try to reason in the same way with regular hexagons, but as it happens, doing the same thing does not always guarantee the same outcome. As figure 6 suggests, the angles refuse to cooperate, leaving annoying empty spots.

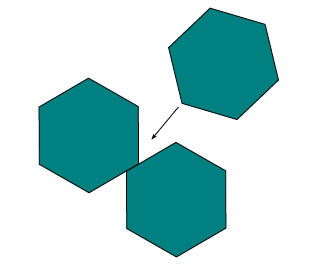
Figure 6: Sliding does not always work.

So, the answer for the triangular wrinkle is yes, while the answer for the hexagonal wrinkle is no. What happens with other regular polygons? A moment's reflection will show that a regular polygon will produce one of these sliding tilings only when its angle divides exactly into 180. Or,

$\frac{180}{180-\frac{360}{n}}$

must be a whole number. Moving around this expression as before, we can see that the viability of the sliding tiling using one regular polygon, goes hand in hand with the condition that

$\frac{n}{n-2} = 1 + \frac{2}{n-2}$

must be a whole number. But $\frac{2}{n-2}$ is a whole number only for $n = 3, 4.$ In other words, only equilateral triangles and squares can produce this kind of sliding tiling using just one regular polygon.

Anything wrong with the pentagon?

You can see how the rules and regulations of mathematics appear very quickly even in the simplest tiling designs. No pentagons in the bathroom floor! No pentagons?

Figure 7: The bathroom floor in Bob Jenkins' house.

Well, let us unveil the secret. We only know that regular pentagons do not work. But, what if we drop the word regular from the specifications? What if we just want to tile with copies of one convex pentagon, which means a five sided shape with all its inner angles less that 180°? If we do, a very different and interesting story will unfold, because there are quite a few convex pentagons that will tile a plane. For instance, how would you like to have one of these patterns on your bathroom floor?

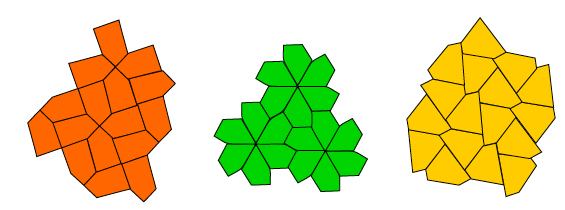
Figure 8: Choosing a pentagonal design.

As you can see, each of them consists of copies of just one convex pentagon. Observe that the third tiling is not vertex to vertex, which is fine. For each of these tilings, we highlight in figure 9 the shape of the convex pentagon tiler and the conditions on its sides and angles.

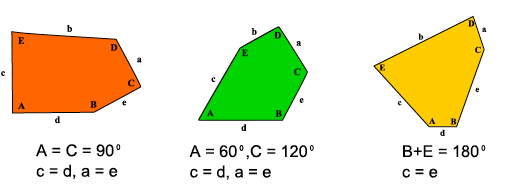
Figure 9: Some good pentagon tiles.

How many kinds of convex pentagons can tile the plane? Before 1968, it was thought that there were five types, which had been discovered by K. Reinhardt in 1918. But between 1968 and 1985 nine new types were discovered. As of today, no new types are known and no one has shown either that the list is complete at fourteen (see here for an illustration of the fourteen known pentagonal tilings of the plane). In other words, the problem of tiling with copies of one convex pentagon remains open. How about trying to come up with other examples of convex pentagon tilers within the known fourteen types? Of course the really serious challenge would be to come up, if possible, with a new type.

Mixed tilings

Summing up, we know now that one regular polygon makes a regular tiling only when it is an equilateral triangle, a square or a regular hexagon. We also know that non-regular pentagons give a lot of choices and seem quite difficult to handle. How about if we get back to regular polygons, but this time we allow more than one shape and size to be used? We have already seen examples of this kind of tilings: tiling (e) in figure 2 uses at each vertex one copy of a square and two copies of a regular octagon, while tiling (f) in figure 2 uses at each vertex one copy of a regular hexagon and four copies of an equilateral triangle.

Figure 2 again: tilings (e) and (f) are mixed tilings.

Inspired by these tilings, we demand of our tilings that polygons with the same number of sides have the same size, that vertices meet at vertices and that the same number of polygons of each shape is used at all the vertices. We will call these patterns mixed tilings. Actually, the three regular tilings (a), (b), and (c) of figure 2 could be considered particular cases of mixed tilings, that use at each vertex four copies of a square, or six copies of an equilateral triangle or three copies of a regular hexagon.

So let's find all possible mixed tilings. As before, we can do it by combining geometry and algebra and, in this case, with some help from a computer. Indeed, let us say that at each vertex a total of $k$ regular polygons meet, with number of sides $n_1, n_2, ... , n_ k$ respectively (note that the numbers $n_ i$ may be repeated). The basic principle is again that the sum of all the angles meeting at a vertex has to be $360^{\circ }$ . Using the formula we found earlier for the angle of any regular polygon, we can write the basic principle as

$\left(180-\frac{360}{n_1}\right)+\left(180-\frac{360}{n_2}\right)+ ... + \left(180-\frac{360}{n_ k}\right) = 360.$

Getting rid of some common factors, we have

$\left(1-\frac{2}{n_1}\right)+\left(1-\frac{2}{n_2}\right)+ ... + \left(1-\frac{2}{n_ k}\right) = 2.$

Or, moving things around,

$\begin{equation} \frac{1}{n_1} + \frac{1}{n_2}+...+\frac{1}{n_ k}=\frac{k-2}{2},\end{equation}$

(1)

which is a rather nasty formula since it has too many unknowns. To simplify things, let us see if we can say something about the number of regular polygons we can use. For starters, the values $k = 1$ or $k=2$ , that is one or two regular polygons, do not work as they lead to the impossible equalities

$\frac{1}{n_1}=-\frac{1}{2}$

and

$\frac{1}{n_1}+\frac{1}{n_2}=0.$

So a mixed tiling has to use no fewer than three regular polygons at each vertex. Could it use any number of regular polygons, say, three, twenty, thirty, two million? Fortunately the answer is no. More precisely, six regular polygons is the maximum number we may be able to use. Regardless of what the combination of regular polygons might be, we know that each regular polygon will have at least three sides. This means that the numbers $n_1, n_2, ... , n_ k$ should all be at least 3. Using this information in (1), we can write

$\frac{k-2}{2}= \frac{1}{n_1} + \frac{1}{n_2}+...+\frac{1}{n_ k} \leq \frac{1}{3}+\frac{1}{3}+ ... +\frac{1}{3} = \frac{k}{3}.$

So, the number $k$ of regular polygons used at each vertex has to satisfy the condition

$\frac{k-2}{2}\leq \frac{k}{3}.$

Solving for $k$ in this inequality we readily conclude that $k \leq 6$ . So, it is true, we cannot have seven or more regular polygons meeting at each vertex. Having settled this point, the next step is to see which combinations of regular polygons are allowed. To do this, we need to find, for each value of $k = 3, 4, 5, 6,$ all $k$ -tuples $(n_1, n_2, ... , n_ k)$ of whole numbers that satisfy (1). Some cases are quite easy to solve, for instance, when $k = 6$ the only possibility is all $n_ i = 3$ (equilateral triangles) since the angle of a regular polygon is at least $60^{\circ }$ and $6 \times 60^{\circ }=360^{\circ }$ (one revolution).

We could, of course, check by hand all other cases, but it's easier to use a computer. See here for a computer algorithm that will do the trick. The algorithm provides the 17 possible solutions listed in the following table:

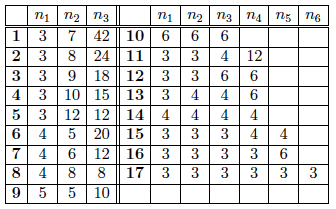
For example, this table tells us that solution 1 uses one equilateral triangle, one regular heptagon and one regular polygon with 42 sides. This makes sense because if we substitute in (1) $k = 3,$ $n_1 = 3,$ $n_2 = 7,$ and $n_3 = 42,$ we get the correct identity

$\frac{1}{3}+\frac{1}{7}+\frac{1}{42}=\frac{3-2}{2}.$

If you wish, you can verify in this way each of the solutions displayed in the table. We notice right a way that solutions 10, 14 and 17 produce the three regular tilings we obtained before (figures 2(a), (b), and (c)). Moreover, solution 8 appears in figure 2(e) and solution 16 appears in figure 2(f). So we know that all these combinations are doable. That is to say, they not only work at one vertex, but they can be repeated again and again at every new vertex, producing a mixed tiling of a plane. This is not the case however, with solutions 1, 2, 3, 4, 6 and 9.

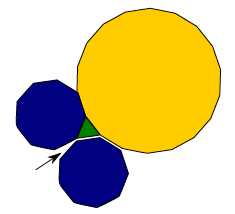
Figure 10: We cannot tile with just the three polygons from Solution 3.

In solution 3, for instance, we can see that once we place the equilateral triangle, the nonagon and the 18-side regular polygon vertex to vertex, as in figure 10, we cannot place a new copy of any of the three polygons that yields a good tiling of the plane. However, we can get a good tiling by combining solutions. For instance, solution 11 cannot work by itself, but when combined with other solutions, like 5, 15, and 17 one gets a good tiling of the plane.

Each one of the other solutions, 5, 7, 12, 13, 15, and 16, produces a mixed tiling of the plane. The catch is that the regular polygons can be rearranged in more than one way! For instance, figure 11 shows two mixed tilings that use solution 12 and figure 12 shows two mixed tilings that use solution 15.

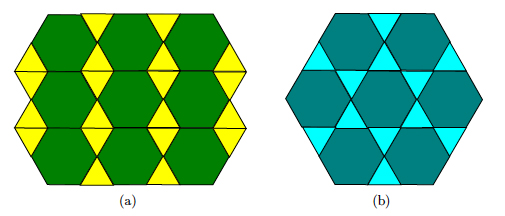
Figure 11: Two arrangements of solution 12.

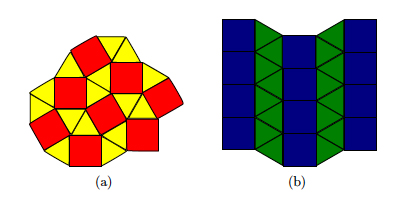
Figure 12: Two arrangements of solution 15.

Observe that in searching for mixed tilings, it is not enough that the shapes work well one vertex at the time, but rather, they have to click at all the vertices simultaneously. Recall that we did not encounter this situation when searching for regular tilings.

Semi-regular tilings

If we now want to eliminate all but a few special mixed tilings, we can make the following additional requirement: at each vertex, the regular polygons should always appear in the same order. For instance, this is the case in figure 12(a), because if we go around any vertex, say, counterclockwise, the regular polygons always appear as a chunk of length five of the sequence ...STSTTSTSTTS..., where S and T mean square and triangle, respectively. Similar chunks can be found in sequences corresponding to figure 12(b) and figure 11(b). However, in figure 11(a), we can see that at some vertices the arrangement is ...THTHTHTHT..., where H stands for hexagon, while at others the arrangement is ...TTHHTTHHTT... .

Here is the final scoop: there are eight mixed tilings that keep the same arrangement at every vertex and are not regular tilings. They are called semi-regular tilings, and they correspond to solutions 5, 7, 8, 12, 13, 15 (two of them) and 16. Solutions 8 and 16 are illustrated in figures 2(e) and 2(f) respectively, while solutions 12 and 15 are shown in figures 11(b) and 12(a) respectively. The remaining three semi-regular tilings are illustrated in figure 13.

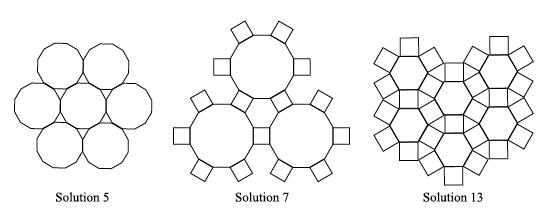
Figure 13: Some more semi-regular tilings.

Useful tilings

You can see that we could go on forever with this tiling business. What if we allow the polygons to get smaller and smaller? What if we use copies of any triangle or copies of any figure with four sides? What if we want to emulate Escher and try to draw some figurative meaning into the tiles? What if we look for patterns that, in some sense, never repeat? Each of these "what ifs", and pretty much any other you may imagine, will open up new fascinating possibilities.

The British mathematician and cosmologist Roger Penrose, for example, has designed non-repeating tilings that now seem to agree with the internal structure of real materials, such as some combinations using aluminum. In a lighter note, Penrose's designs have also caught the attention of a toilet paper manufacturer, because paper embossed with a non-repeating pattern can be rolled without leaving bulging spots. But Penrose had copyrighted the pattern and the manufacturer got a legal spank.

Beyond the fun side of tiling and its more, or less, serious applications, Penrose's interest in tiling relates also to his interest in artificial intelligence and the works of computers. For instance, the tiling problem, that is, whether a given bunch of shapes will tile a plane, belongs to a class of mathematical problems called non-recursive. The tiling problem is answerable in each particular case, but, Penrose says, "there is no systematic procedure that, once implemented on a machine, could give an answer in any case, without requiring any more thinking."

From looking at pretty pictures or making them, to doing mathematics, the choice is yours. For now, we draw the line here.

About the authors

Josefina (Lolina) Alvarez was born in Spain. She earned a doctorate in mathematics from the University of Buenos Aires in Argentina, and is currently a professor of mathematics at New Mexico State University in the United States. Her research interests lie in the areas of functional and harmonic analysis. She is on the editorial board of Matematicalia and writes the column What if...?. She likes to hike, and with husband Larry and dogs Brandywine and Sofia, she has walked many kilometres along the beautiful trails of New Mexico and elsewhere. You can read more about her on her website.

Cesar L. Garcia was born in Mexico City. Under the supervision of W.B. Johnson he obtained his Ph.D. at Texas A&M University. Currently he is a full time professor at Instituto Tecnologico Autonomo de Mexico (ITAM) in Mexico City. In addition to research in functional analysis (geometry of Banach spaces in particular), he enjoys writing mathematical exposition and to participate in juries in national and international mathematical olympiads for kids.

Plus.Maths.org