
Abel Prize 2018: the power of asking good questions
In 1967 a 30-year-old American mathematician, still in the early stages of his career, wrote a 17 page letter to the eminent French mathematician André Weil. The covering note that he sent with the letter said:
"After I wrote [this letter] I realized there was hardly a statement in it of which I was certain. If you are willing to read it as pure speculation I would appreciate that; if not – I am sure you have a waste basket handy."

Robert Langlands (Image Dan Komoda/Institute for Advanced Study)
The letter may have contained many unproved statements, but these turned out to be asking questions that would create a whole area of mathematical research, unmatched in modern mathematics for its scope, deep results and sheer size in terms of the number of mathematicians it has enticed. The author of the letter – Robert Langlands – has been awarded the 2018 Abel Prize for his "visionary program" that bridges previously unconnected areas of mathematics, and is now frequently described as a "grand unified theory of mathematics".
The insights contained in Langlands' letter to Weil, and more fully in his 1970 lecture Problems in the Theory of Automorphic Forms, set out a programme of research that is now referred to as the Langlands program. Langlands made a number of conjectures about the connections between two previously unrelated areas: number theory and harmonic analysis.
From waves to numbers


The sound wave from a tuning fork (top), compared with that of human speech (bottom).
Harmonic analysis explores how functions and signals can be represented as a sum of waves. For example, the sound wave of the middle A on a tuning fork is a perfect example of a sine wave, written mathematically as sin(x). The sound wave of speech is more complicated. But any sound wave, indeed any repeating function, can be broken up into a number of sine waves of various frequencies and intensities, thanks to work that started with Joseph Fourier, in the eighteenth century. (You can read more about this here.) Automorphic forms are a more generalised version of periodic waves, like the familiar sine wave, which operate in more complicated geometric settings.
A large area of number theory – the study of numbers and their properties – is concerned with certain types of solutions to equations. For example, you might remember the quadratic formula from school which gives a way to solve any quadratic equation: the equation $$ ax^2+bx+c=0 $$ (where $a$, $b$ and $c$ are real numbers) has the solutions $$x_1 = \frac{-b+\sqrt{b^2-4ac}}{2a}$$ and $$x_2 = \frac{-b-\sqrt{b^2-4ac}}{2a}.$$
Évariste Galois, in the nineteenth century, began the mathematical study of symmetry by looking at the symmetries that are generated by solutions to equations. For example, the quadratic equation $x^2-2=0$ has two different solutions $\sqrt 2$ and $-\sqrt 2$, but you can see there is a kind of mirror symmetry between them. The Galois group of an equation is the group of symmetries that arise in a mathematical object that is generated from the solutions of the equation. (You can read more here.)
Langlands proposed a bridge between harmonic analysis and number theory built on the relationship between Galois groups and automorphic forms. A particularly famous example of this correspondence comes from Andrew Wiles' proof of Fermat's last theorem, announced in 1997. Wiles actually proved a more general result known as the Taniyama-Shimura-Weil conjecture, that related the number of solutions of a particular type of equation, called elliptic curves, to a type of automorphic form called modular forms, mathematical objects that are symmetric in an infinite number of ways. (You can read more here.)
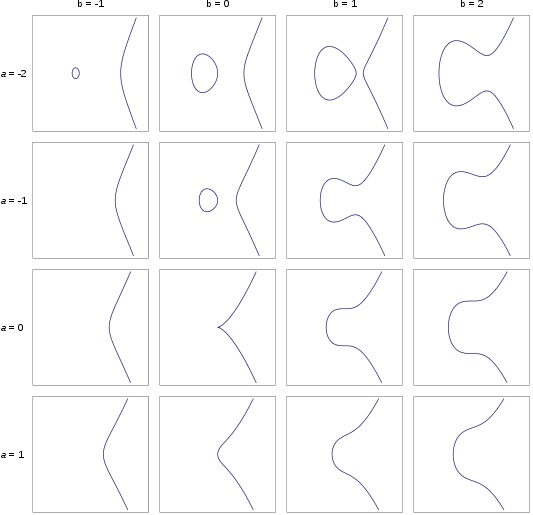
Elliptic curves are the equations that can be written as y2=x3+ax+b. The real solutions of these are shown in this figure for different values of a and b.
This year's Abel Prize recognises Langlands' insight and ability to pose such fruitful questions. Since that letter in 1967, hundreds of mathematicians have been inspired by Langlands program. There has been success in proving some aspects of the program, including deep results by Vladimir Drinfeld, Laurent Lafforgue and Ngô Bào Châu – whose work was recognised by Fields medals. But core parts of the programme remain unsolved and are still the subject of intense mathematical research. By asking the right questions and providing a map to answer them, Langlands has inspired some of the most fundamental mathematics of the last 50 years.
You can find out more about the Abel Prize and Langlands work at the Abel Prize website and the Institute for Advanced Study.