
Building meaning: dog or ostrich
A key part of building a model of the world is how we build meaning. Children quickly understand what the word "dog" means from seeing just a few examples in pictures or real life. They build higher level representations – alive, animal, four legs, furry – intuitively. And they can generalise easily: a dog with one leg missing is still a dog despite only having three legs. They can very quickly learn which animals are, and aren't, dogs. Children can build these higher levels of understanding from remarkably small data sets, and can adapt to changes in their datasets (seeing different types of dogs, or different types of animals) quite quickly.

This is not a dog. In fact, it has never been a cat either. It was created by a machine learning algorithm at thiscatdoesnotexit.com
Machines are only recently getting better at this, and only thanks to the advent of deep learning. Yoshua Bengio received the 2018 Turing Award for his breakthroughs that helped make deep learning a critical part of machine learning and artificial intelligence.
Machine learning refers to when a machine learns how to do a specific task itself, rather than being explicitly taught how to do it by human programmers. Since the 1980s neural networks have been used as the mathematical model for machine learning. Inspired by the structure of our brains, each "neuron" is a simple mathematical calculation, taking numbers as input and producing a single number as an output.
These neurons are arranged in layers: the neurons in a layer receive as an input a weighted sum of the outputs of neurons in the previous layer. Humans decide the structure of the network, but not the weights in these weighted sums. Instead, these are learnt through a training process that runs a large set of examples through the network, tweaking the weights to achieve the best outcomes for the given task. (You can read more in What is machine learning?)
Originally the neural networks used in machine learning were relatively simple, consisting of only one or two layers of neurons due to the computational complexity of the training process. But in the early 2000s Bengio and colleagues began to work on what they called deep learning: "We found a few tricks to train neural nets that had more layers than was thought possible."
Distributed representations
Deep learning has an advantage over other machine learning methods; it gives machines the ability to build good representations. A representation is the way the machine stores a concept. In classical artificial intelligence (before machine learning) humans taught the machine the knowledge they needed. The algorithms were like a set of rules that were written by the human programmers, and concepts were represented symbolically (such as having a variable "cat" set to 0 if something isn't a cat, and set to 1 if something was a cat). Deep Blue, the chess playing computer built by IBM that beat chess grandmaster Garry Kasparov in the 1990s, is an example of this sort of classical artificial intelligence.
A key idea in deep learning is that concepts can be instead represented as a vector (an array of values) – a distributed representation. The word "cat" can be represented by the vector:
| [-0.241414, 0.287426, 0.165113, -0.431581, -0.087530, 0.561078, -0.415193, 0.003364, 0.016638, 0.030558, 0.137265, -0.101964, -0.144205, 0.200312, -0.440345, 0.782978, 0.215758, -0.397508, -0.132525, 0.392892, 0.187668, 0.190704, -0.597705, -0.473172, -0.046912, -0.655475, 0.297324, -0.044785, 0.907623, 0.090989, 0.330201, -0.218510, 0.442974, -0.197005, -0.013970, -0.048274, 0.016939, -0.304073, -0.458688, 0.839282, 0.364900, -0.573024, 0.130873, -0.267990, 0.109434, 0.146609, 0.497982, -0.281677, 0.415757, -1.341299, 0.755230, 0.274921, -0.261315, 0.316203, -0.266019, 0.077696, 0.086259, -0.148955, 0.111285, 0.905508, -0.499343, 0.220561, -0.060084, -0.138308, 0.263414, 0.029885, -0.030825, -0.700774, -0.250947, -0.387521, 0.167361, -0.278134, -0.658570, -0.117905, 0.114435, 0.236835, 0.319998, -0.212485, -0.675103, 0.043290, -0.045866, 0.771321, 0.205061, -0.775832, 0.429374, 0.097047, 0.065185, 0.233347, -0.138985, -0.095526, -0.002476, 0.221378, -0.443003, -1.068492, -0.282422, -0.356644, -0.192903, -0.000860, -0.015085, 0.294197, 0.318298, -0.105752, 0.045668, -0.191743, -0.108592, -0.211702, -0.278396, -0.444925, 0.075270, -0.043502, 0.372264, -0.520599, -0.189202, -0.411445, 0.320581, -0.242174, -0.208912, -0.571741, -0.146618, 0.231338, 0.077776, 0.508152, -0.499199, -0.345736, 0.026528, 0.228578, -0.790778, -0.094263, 0.304350, 0.644286, 0.559164, 0.067319, -0.223100, -0.267459, -0.116927, 0.696897, -0.250773, -0.339711, 0.295284, 0.148529, 0.139849, -0.526502, 0.379415, -0.517519, 0.025815, 0.136009, -0.090450, 0.061950, -0.496813, 0.326041, 0.528336, -0.664441, 0.888717, -0.210583, 0.210085, -0.250152, -0.464110, -0.398434, -0.097318, -0.136705, 0.734923, 0.024840, 0.186065, 0.656894, 0.442599, 0.538127, 0.598445, 0.550830, 0.608239, -0.210517, 0.262453, -0.103285, -0.163599, -0.091919, 0.283204, -0.239344, 0.328113, -0.064806, -0.206737, 0.552150, 0.391778, -0.137410, -0.270437, 0.440234, -0.623495, -0.064421, 0.352393, 0.086501, -0.191278, -0.642643, -0.126353, 0.180774, -0.417938, -0.199682, -0.310765, 0.267943, 0.419079, -0.060403, 0.264354, 0.033174, 0.114115, -1.067016, 0.102984, 0.220216, 0.196559, -0.061410, 0.074493, 0.447212, -0.018113, -0.605357, -0.660194, 0.019961, 0.547134, 0.048423, -0.077267, 0.035326, 0.410081, -0.600771, 0.138824, 0.377122, -0.396284, 0.173469, 0.525796, 0.276606, 0.344208, 0.553607, 0.018219, -0.085965, 0.190523, 0.099517, 0.636050, 0.756199, -0.295487, -0.309625, -0.140817, -0.497444, -0.403202, -0.304629, -0.128906, 0.153457, 0.845987, 0.190644, 0.217209, 0.054643, -0.063143, -0.057904, 0.143839, -0.300590, -0.399825, 0.106663, 0.235159, 1.040565, -0.074484, 0.324786, -0.257785, 0.673381, 0.097968, -0.361923, -0.282786, 0.173656, 0.334292, 0.083597, 0.048122, -0.148704, 0.443468, 0.240980, 0.264529, 0.165889, -0.219577, 0.309359, 0.134012, -0.141680, 0.023127, -0.058023, 0.074283, -0.490581, 0.288622, 0.284951, 0.066673, 0.302247, 0.081319, -0.383685, -0.052862, 0.244946, -0.344482, -0.072416, 0.804204, -0.042981, -0.226182, 0.482332, -0.163026, -0.414333, -0.399022, -0.424497, -0.245093, -0.040660, 0.263090, 0.326652, -0.317213, 0.222228] | = |
And most importantly, the vector representation is not given to the machine by humans, it is learnt by the machine after working through sets of training data. For example, the GloVe unsupervised learning algorithm can be trained over the dataset of all wikipedia articles, to learn vectors for every word in this data set. (You can read more in this excellent article by Jay Alammar, and we'll use this data set of GLoVe trained on wikipedia, as our example from now on.)
Deeper meaning
Learning distributed representations allows the machine access to higher levels of meaning of their vocabulary. Similar words are closer together, when you consider the word vectors as location for words in a higher-dimensional space. For example, the closest words to "frog" for a machine trained in this way are: frogs, toad, lizard, litoria, leptodactylidae, rana and eleutherodactylus (the last four all being specific species of frog). Their proximity means they all have very similar values for every entry in their word vector. But just having similar values across some of the entries in a word vector can give the machine access to higher levels of meanings, as demonstrated by the illustration, by Jay Alammar, below. Alammar uses colours to represent the numerical values in a word vector, from red for the highest values, through white for zero, to blue for the lowest values.
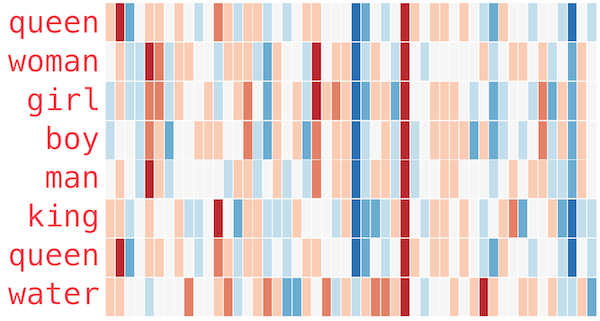
Illustration of word vectors from the article by Jay Alammar (CC BY-NC-SA 4.0)
Geometrically, a similar value in a particular entry means that the words represented by these vectors all fall into a line, in a sense, in a particular direction. Computer scientists use a statistical technique called principal component analysis to identify these geometric features in the vector space of words. We can imagine how these geometric features might line up conceptually too. Similar values line up for all the words indicating people, and within these we see more similarities for those indicating woman and girl, or boy and man. The geometric features in the distributed representations of these words allow machines to learn more abstract, higher levels of meanings of the words.
Remarkably, these sort of word embeddings in a vector space can even lend themselves to a certain sort of word arithmetic. This is commonly illustrated by the example of using vector addition to solve: "king" - "man" + "woman". Despite the machine never having been given the meaning of these words, the distributed representations allow the machine access to higher level meanings, such as the gender of words. The closest word vector to the answer to this calculation, in our example dataset, is "queen".
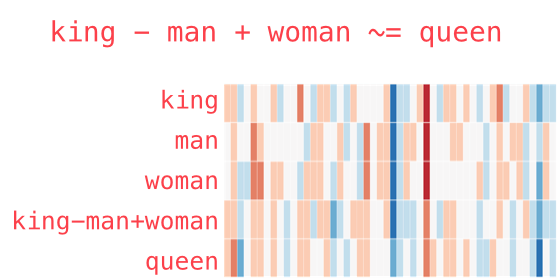
"Queen" is the closest word to the result of the vector sum of "king-man+woman" (Image by Jay Alammar – CC BY-NC-SA 4.0)
In a similar way, machine learning algorithms can be trained on data sets of images, rather than texts, to learn distributed representations of images. (You can find out how they might do this in Face to face.) In this case an image may be represented by a vector, and the aim of the machine learning algorithm would be to cluster together the vector representations of images of similar things.
The vector representations of images of cats would cluster together, and that cluster might be close in some way to the cluster of images of their fellow mammals, dogs, and be further from the cluster of images of frogs. And similar values in certain entries of the image vectors would correspond to certain shared features in the images. This has led to great advances for image recognition, such as distinguishing between gendered features in images, just as the GLoVe algorithm learnt about gendered words. But machines are still far from human level AI. It's still possible to intentionally fool a machine by switching off just a few pixels in an image, which would never even be noticed by the human eye.

Although these images look identical to us, to a machine just a switch of a few pixels could fool an image classifying algorithm. (Image from Bengio’s HLF 2019 lecture – used with permission)
Acting to understand
Deep learning has given machines a way to learn these distributed representations and enable them to create new higher level knowledge about the world. "A big payoff of deep learning was that it allowed learning of higher levels of abstraction," says Bengio. This has led to machine learning advances in working with languages and images, such as generating realistic images based on text descriptions.

An example from the AttnGAN algorithm, created by Xu et al in 2018. (Used with permission)
(You can see some of these machine learning algorithms in action for yourself, generating people and cats that have never existed, trying to spot real from fakes, and generating some AI art.)
If the data is represented in the right way, it enables machines to build better models of the world, and to start to tackle questions humans care about, taking us a step closer to true artificial intelligence. Also, having a good internal model of the world, will help enable machines to interact with the world, to have agency. "The things that we can control through our agency should be things we can name, that we can represent at a higher level," says Bengio. But in a circuitous way, Bengio believes that machines will need agency to build a good model of the world. Bengio and his colleagues believe that in order for machines to move beyond weak artificial intelligence, they will need to be able to interact with the world, influencing and adapting to the data they receive - something called the agent perspective . "In order to build machines which construct an internal understanding, an internal representation of how the world works, I and others believe they need to interact with the source of the data, they have to interact with their environment [that creates] that data. That's the agent perspective."
Bengio continues to lead this area of research into giving machines such agency, but it is still a very new field. "The agent perspective is something that is embraced in reinforcement learning, which is a particular branch of machine learning. In other camps of machine learning we tend to ignore it... We haven't [yet included] the experience of agents in the environment to improve deep learning and build better models and representations of the world." At some point in the future we might have that opportunity – to meet, and interact with, these machine learning agents. And when we do, perhaps that will be an opportunity for us to learn more about ourselves.
About this article
Rachel Thomas is Editor of Plus. She spoke to Yoshua Bengio at the Heidelberg Laureate Forum in September 2019.
This article now forms part of our coverage of a major research programme on deep learning held at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

