Career interview: Systems engineer
A version of this interview is also available as a podcast.
"I am a systems engineer for the Lockheed Martin UK," says Chuck Gill, chatting to Plus at his office just around the corner from Victoria Station in London. "At the moment we are working with the Department of Transport to help travellers get from one point to the other a little more effectively."
That's the present, but we will start our story a little further back in the past. Back then, rather than puzzling over carbons emissions and 2012 Olympic traffic, Gill had his sights set firmly on the stars — he wanted to become an astronaut.
"I had a life-changing day in 1961 when I saw Alan Sheperd [the first American in space] go up. My mum made me late for school; she made me sit there and watch Alan Sheperd launch. And ever since then I've had that bug about space. It seemed like the best way to become an astronaut was to study physics, and that's what I did."
Gill himself never made it up to space himself ("My eyes went bad"), but he got closer to space than most of us ever will. After completing his degree and two Masters in nuclear physics and electrical engineering at the American Air Force Academy, he started work on satellite programmes, interspersed with stints as a navigator for the US Air Force. "I was alternating between satellite jobs and flying jobs, and in both of these mathematics was critically important."
Sky maths
Hang on. Maths important in flying jobs? On board high-tech US bomber jets? Surely it's just a matter of tapping a few co-ordinates into a computer? "Oh no, we did it all by hand. Even these days, with GPS and inertial navigation systems, you never know when these might fail, so [the Air Force] still practise doing things by hand."
"Imagine you're 6000 miles from Los Angeles, somewhere above the Pacific Ocean, in front of a thunderstorm. The only way to figure out how to go off course and avoid the thunderstorm, and still get to the tiny island you're supposed to land on is by celestial navigation."
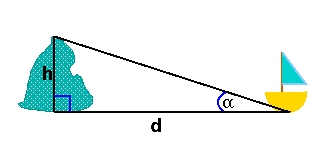
Figure 1: The rock has height h and you've measured the angle α. We have tan(α) = h/d, where d is the unknown distance between ship and rock. This gives d = h/arctan(α).
Celestial navigation uses the stars as "landmarks" to help you figure out where you are. As an analogy, imagine that you're on a ship at sea. In the distance you can see a familiar rock; you know which rock it is and can look up its exact location on the map and also know its height. The top of the rock, the bottom of the rock and the point on the surface of the sea at which you're sitting form a right-angled triangle. You can measure the angle at the corner of the triangle defined by your own location. Now you know two angles (the right angle and the one you've just measured) and one side of the triangle (the height of the rock), so using trigonometry you can figure out the length of the other two sides. In particular, you can figure out your distance from the rock (see figure 1).
If you can do the same for another landmark, then you know your distance from two known locations. You can then find your own location by drawing circles around the locations of the two rocks on your map, with radii given by the respective distances. The circles will intersect, usually in two points, so with a little extra information, you can figure out exactly where you are.
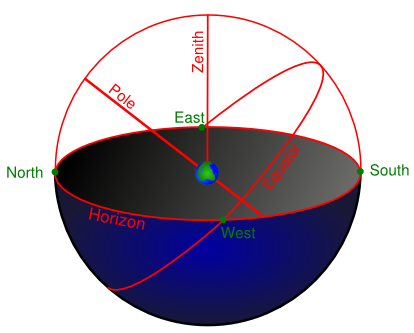
The celestial sphere. Image from Wikipedia.
Celestial navigation works along similar lines, although it's slightly more complicated. You have to take the rather old-fashioned view that all the celestial bodies live on a celestial sphere; a sphere that is concentric with the Earth and encloses it. By picking two stars whose location on the celestial sphere you can look up in charts, measuring the angle they make with the horizon, and solving triangles that lie on the celestial sphere, you can deduce exactly where you are. The triangles in question now lie on the surface of a sphere — they are spherical triangles — so the trigonometric identities are slightly more complicated than those for plane triangles.
People have been navigating by the stars for centuries, but the speed of modern planes adds an extra complication: "You take a two minute observation of each star, the hour has sixty minutes, and your plane is moving at 600 miles an hour, so when you've finally finished your calculations, you know where you were ten minutes ago, which may or may not be a good thing. So you just have to keep repeating the process during your ten-hour flight across the Pacific."
Space maths
When it comes to satellites, the celestial sphere, despite its poetry, clearly won't do. You need to consult the laws that govern the behaviour of bodies moving around in three-dimensional space. "This is where Kepler's laws become extremely important," says Gill.
The German mathematician and astronomer Johannes Kepler established his three laws for planetary motion at the beginning of the seventeenth century. Incidentally, it was Kepler who coined the term satellite, though he was referring to the moons of Jupiter, rather than the lumps of high-tech wizardry we think of today.
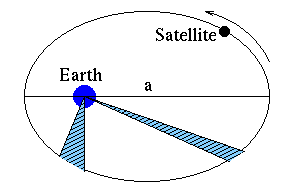
Kepler's laws: satellites have elliptical orbits with the Earth at one of the foci of the ellipse. The shaded areas illustrate the second law. The semi-major axis of the ellipse is half of the axis labelled a.
Kepler's first law simply states that a body in orbit (for example a satellite) traces out an ellipse, and that the body it is orbiting (for example the Earth) is at one of the foci of that ellipse. The second law states that a line joining the two bodies sweeps out equal areas in equal time. This means that a satellite travels faster when it is closer to the Earth than when it is further away from it. The third law relates the time the orbiting body takes to complete a full circuit, also known as the body's period and denoted by p, to the length l of the semi-major axis of the ellipse: it states that p2 is directly proportional to l3. This means that satellites that stray further from the Earth take longer to complete a full circuit than those that stay closer to it.
Despite their grand old age and the revolutionary interventions of Newton and Einstein, Kepler's laws are still the first port of call for satellite operators.
But that, of course, isn't all the maths that's used in satellite operation. "Satellites are royal pains in the guess what," says Gill. "Today is June the 20th, and I tell you, every satellite operator in the world, whether it's the person who does TV, or the person who does telephone, or whatever else, is having a really bad day. This is because today is the summer solstice. One of the hardest problems concerning satellites is that they are either being baked by the Sun, or they are freezing. You need to find out if the sensitive satellite equipment — radio receiver, battery, gyroscope, fuel cell — is going to freeze or bake." At a solstice, the Sun reaches furthest to the North (in the summer), or furthest to the South (in the winter). "What happens at the solstices is that you have extremes. The satellite is experiencing either extreme heat or extreme cold."
The heat equation
\ Let $u(x,y,z,t)$ denote the temperature at time $t$ and at the point $(x,y,z)$ of a given object. The heat equation is $$\frac{\partial u}{\partial t} = k (\frac{\partial^2u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}).$$ Here $k$ is a constant encoding the thermal conductivity of the object. When solving this partial differential equation to find the function $u$, you need boundary conditions that specify temperature at time zero at certain points of the object. It's these boundary conditions that carry information on the source and intensity of the heat acting on the object.
With these kind of temperature variations, it becomes essential to model the heat flow through the satellite. There's a heat equation that describes the flow of heat through a given object. It's a partial differential equation, because a flow of heat is described by the way temperature changes as time passes: if u(x,y,z,t) is the temperature at point (x,y,z) at time t, then the flow is given by the partial derivative of u with respect to time. What you're after is the function u, so that you can determine the heat at any given point at any given time. It's not always possible to solve the heat equation analytically to find u, so you have to use numerical methods to approximate solutions, and that involves thousands of measurements and calculations.
"You have to spend hundreds and hundreds of hours running those calculations [when you're building the satellite]. And sure enough, you get it up there and something was wrong. Your assumptions on solar radiation were wrong, or your assumptions on how the metal propagates heat was wrong. So if you meet a satellite operator today and ask them if they had a bad day, they probably did."
Intelligent maths
The exact details of Gill's work on satellites are classified, since the work was related to military operations. From satellites, Gill moved on to an even more secret world: that of military intelligence. Cryptography is probably the first thing to spring to mind when you think about intelligence and mathematics. The Allied success at cracking the German Enigma code in World War II is well-documented on Plus (see the article Exploring the Enigma or listen to the podcast Codes and codebreaking - the Enigma machine), and, as Gill informs us, there is an American/Australian counterpart: after the Enigma success, US and Australian intelligence managed to crack the Japanese Purple cypher.
Gill's own work on intelligence, however, was more to do with statistics than cryptography. "Probability theory and statistics are very important. How do you know your data is good? How do you know you've got the right kind of data? Can you assign a probability of fact to whatever it is you're doing? Can you quantify your uncertainty? Since you have uncertainty associated to each possible action, things soon get very complex."
Uncertainty isn't only an issue in intelligence of course. It's around whenever you apply mathematics to the real world, and being able to quantify it is hugely important. "I had a very good professor back at graduate school. He used to beat us incessantly about uncertainties. You'd put your answer down and he'd say 'I don't care if your answer's right, your uncertainty is wrong, so zero credit.' Of course we hated him. But in the intelligence world and also the satellite design world, uncertainty is what saves your life. If you say the thing you're looking for is three feet away, plus or minus a hundred feet, that's useless information. But if you say plus or minus a micron, then that's probably very good."
Earth maths
These days, Gill deals with civilian uncertainties. After leaving the US Air Force, he started working for Lockheed Martin. He relocated to the UK four years ago. "Whilst I'm in the UK, I'm working with the Department of Transport, trying to find better ways of taking various sources of transport information, mashing them together and helping a traveller get from one point to the other a little more effectively. There may be some applications for the [London 2012] Olympics, don't know yet, but we're hoping to go that way. There are definitely some implications for reducing carbon emissions."

Getting people from A to B effectively.
Gill is working on systems that will allow passengers to enter their journey data into a computer or mobile phone, and receive complete information on the various routes and modes of transport they can choose, complete with arrival times and information on what a particular journey does to their carbon footprint. "You can do some of this for buses and trains already, but how do you do this when you're mixing your car with your train, with your airplane? That's the kind of thing we're working on."
The carbon problem is particularly difficult: "Suppose that someone gets on a train and assumes that their carbon emissions are low, because they are taking the train, rather than the car. But what if it's a twelve car train and you're the only person on it? Think about the amount of electricity that is needed to move that train. What's the source of that electricity? If it's a coal fire plant in the North, what is your carbon footprint then? What about the steel in the train and the rails, how much carbon was emitted in their production? But if the train is full, then the individual carbon footprint is probably very low. How do you solve that problem? That's the kind of thing we're trying to study and come up with answers for. Let people make the right decision based on the right data." Gill's team have already come up with a preliminary system that allows users to specify their main concern — speed, cost, or carbon emissions — and are currently working on refining it.
Statistics — data collection, data mining, data integration, etc — are obviously hugely important in this work, but so is the maths of chemistry and physics: "Determine the carbon content of the power generation and the train construction, determine the carbon content of a Diesel powered taxi versus a petrol powered Ford Focus, or the carbon content of a bus. What is the load of the bus? You can do maths forever on this."
Universal maths
If one thing has remained constant in Gill's varied career, it's the importance of mathematics. "I studied physics because physics is maths. It's the application of maths to the real world." But despite the universality of maths, Gill finds that when it comes to recruitment, it can be hard to find people who are sufficiently mathematically skilled. "This really befuddles me. I've used maths in pretty much everything I've done in the thirty years since leaving university. But when you go to universities you see some students who are very much in love with mathematics, but the majority are not. They want to go into business, but you can't do business without mathematics; they want to work on green initiatives, but we just talked about how you can't do that without mathematics. So I hope that things like Plus help to encourage people to study it."
So what about Gill's future? He still has lots of work to do at Lockheed Martin, but there's another thing he'd like to get into: "I think anybody who's had a career like I have really needs to go into education later on and teach those life lessons. The best teachers I had were not the ones that said, 'This is what the book says we are going to do today'. I give you a perfect example: I went to the Air Force Academy right after the Vietnam war and after the Moon landings. The guy who really got me to understand the equations of lift and drag [in aerodynamics] was a guy who had actually been flying a fighter plane over North Vietnam during the worst part of the war. He said, 'You may think this is crap, but let me tell you, if you don't understand the effect that indicated air speed has on your lift equation or your drag equation, you are going to die'. "
"Or you meet David Scott, who walked on the Moon, and he says, 'Ok, I've got this much more oxygen in my suit, and the lunar module is this far away, and the lunar vehicle goes ten miles an hour, am I going to get back in time?' If a teacher can give you real lessons that are exciting, that really shows you that maths is important."
Don't forget that a version of this interview is also available as a podcast.
About the author
Marianne Freiberger is Co-Editor of Plus.