Chaos on the billiard table
Even simple processes can lead to chaos. That's why it's so hard to predict the weather, the stock market, and all sorts of other processes we come across in everyday life. Mathematicians try to come to grips with chaos by looking at the simplest systems that exhibit it. One beautiful example is the game of billiards.
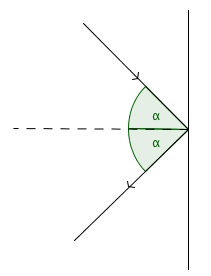
The law of reflection: the angle of incidence equals the angle of reflection.
"Mathematical billiards is an idealisation of real billiards," explains Corinna Ulcigrai, a mathematician at the University of Bristol who has studied mathematical billiards. "The idea is similar: you have a table and a ball, but the ball has no mass so there is no friction. The ball bounces around according to the same rules as an ordinary ball." That is, it moves along a straight line until it hits the edge of the table where it bounces off following the law of reflection (see the figure on the right). But unlike in real billiard, there are no pockets that can swallow the ball, and since it doesn't experience any friction the ball will keep going forever.
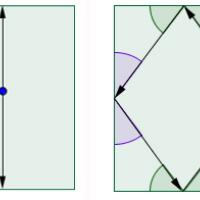
What will the trajectory of a ball typically look like? "If you shoot the ball so that it hits one of sides of the table head-on (its trajectory forming a right angle with the side), then it will return along the same trajectory it arrived on, but travelling in the opposite direction. It will carry on to hit the opposite edge at the exact opposite point, retrace its path, and keep bouncing between the two opposite points along the same straight line forever. Similarly, by getting your initial direction just right, you can make sure that the ball bounces off the mid point of all four edges in turn and then returns to where it started, travelling along the same four line segments forever.
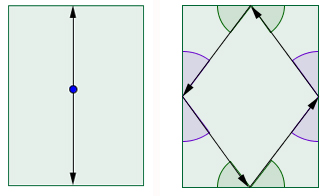
Left: if you shoot a ball so it meets the wall at right angles, it will bounce between opposite points on the table forever. Right: similarly, you can make the ball travel between four points. These are examples of periodic trajectories.
But it turns out that this regular behaviour is very rare. In the 1980s mathematicians proved that for the vast majority of initial directions the trajectory will be much wilder: not only will it not retrace its steps, but it will eventually explore the whole of the table, getting arbitrarily close to every point on it. What is more, a typical trajectory will visit each part of the table in equal measure: if you take two regions of the table whose areas are equal, then the trajectory will spend an equal amount of time in both. This behaviour is a consequence of billiards being ergodic. By "vast majority" mathematicians mean that if you pick a direction at random, it will almost certainly behave in this ergodic way.
Ergodicity of billiards means that it's really hard to predict where a ball will be after a given amount of time: in order to find out, you have to literally trace its path on piece of paper, meticulously measuring angle after angle, because you can't rely on any regular pattern to kick in. That might not appear too bad, after all you could program a fast computer to do the work for you. But there is another, independent feature that makes things difficult. If you get the initial conditions of the ball — the place and direction it starts out with — ever so slightly wrong, then the little error will generally snowball, rendering your prediction inaccurate. This sensitive dependence on initial conditions is popularly known as the butterfly effect, and is one of the hall marks of chaos.
Not just fun and games
As far as real billiards goes, chaos is probably what makes it fun. Who wants to play a predictable game? But mathematicians don't study billiards because they like playing it. Variations of the game are models for dynamical systems that occur in nature. The notion of ergodicity was developed in the context of particles, for example the molecules that make up a gas, bouncing around an ambient space, bumping into each other as they go. "Ergodicity is a very important property of chaotic systems," explains Ulcigrai. "It dates back to the 19th century when the physicist Ludwig Boltzmann suggested that many dynamical systems are ergodic: they are so chaotic that if you look at the trajectory of a typical point this will in some sense explore all [of the possibilities that are theoretically allowed]."
Surprisingly, though, ergodicity can make your system more predictable. There is a mathematical result called the Birkhoff ergodic theorem which tells you that if a system is ergodic, then even though you can't predict precisely what it will do in the future, you can accurately predict average quantities for typical trajectories. For example, in billiards, you might not be able to predict exactly where a ball will be after some time has elapsed, but you can accurately predict what proportion of its time it spends in a certain region of the table. If it's a gas you are looking at, then you might not be able to say exactly where its many constituent molecules are at any given moment, but you can predict things like its temperature or pressure. So, as chaotic systems go, ergodicity is actually a good thing.
Changing shape
One natural phenomenon that quickly turns into a billiard problem when you simplify it is the electrical conductivity of metals. An electric current is a flow of particles called electrons. To make things simpler, suppose there's just a single electron passing through the metal, and imagine the metal as a lattice of molecules evenly arranged in the two-dimensional plane. If you think of the electron as a little ball, then it behaves just like a billiard ball bouncing around on a table that contains a lattice of obstacles.
Three possible trajectories of a ball on a table with round obstacles. Image courtesy Jens Marklof, from Kinetic transport in crystals. Used by permission.
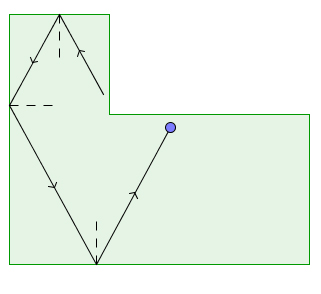
The beginning of a trajectory on an L-shaped table. The angles in this table are all rational multiples of π, namely π/2 (five of them) and 3π/2 (the remaining one).
To study systems such as this one you need to let go of another familiar feature of the billiards game we encounter in pubs: the rectangular shape of the table. A good starting point is to ask what happens if the table is triangular, hexagonal or L-shaped. More generally, what if your table is a polygon, a shape whose edges are straight lines, and which might contain holes that correspond to obstacles? Is the result above — that typical trajectories are ergodic and evenly distributed throughout the table — still true? The answer is yes, as long as the angles in the corner of the polygon are of a special form. They must be equal to $p/q \times \pi$ where $p$ and $q$ are whole numbers (so that $p/q$ is a rational number). Rectangles and squares fall into this class (their corner angles are $1/2 \times \pi$) and so do equilateral triangles (their corner angles are $1/3 \times \pi$), regular pentagons (with corner angles of $3/5 \times \pi$), regular hexagons ($2/3 \times \pi$), as well as all other regular polygons. But the result also holds if the table contains obstacles, as long as these are also bounded by straight lines and the angles in the resulting polygon are all of the form above. Billiards played on a table which satisfies these properties is called rational polygonal billiards.
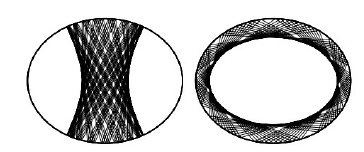
Examples of trajectories on a convex shape. They do not explore all of the table. Image courtesy Carl Dettmann, from his article in Frontiers in the study of chaotic dynamical systems with open problems. Used by permission.
If you allow the lines that bound the table to be curved, however, the system changes gear altogether. It turns out that the game is a lot less chaotic if the table's boundary bulges outwards everywhere (if it is strictly convex). Examples are a circle or an ellipse. In this case, there are many more periodic trajectories — those that retrace their steps — and trajectories don't tend to explore all of the table.
If, on the other hand, the shape contains pieces of boundary that bulge inwards, then the game becomes a lot more chaotic. If you consider a small range of initial positions and directions of the ball, then not only do the resulting trajectories diverge, but they diverge to such an extent that they will eventually be evenly distributed over all of the table. So a small inaccuracy in initial conditions means that you really have no clue where the ball will be after some time — this is an example of a property of dynamical systems called mixing.
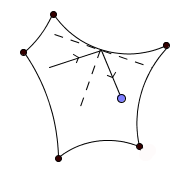
The beginning of a trajectory on a concave table.
Rational polygonal billiards therefore represents a watershed between different levels of predictability. "Polygonal billiards is dynamically interesting because it displays a kind of slow chaos," explains Ulcigrai. "It is chaotic, but less chaotic than others."
Infinite surprises
Perhaps surprisingly, it took mathematicians longer to prove results about polygonal billiards than for billiards with curved shapes. Results about the ergodicity curvy billiards were proved back in the 1960s, not least by Ulcigrai's PhD supervisor, Yakov Sinai, who received this year's Abel Prize, one of the most prestigious prizes in maths, for his contributions to dynamical systems theory. It wasn't until the 1980s that mathematicians came to grips with seemingly straight-forward polygonal tables. Their success is down to an ingenious mathematical trick, which turns those jagged and wild trajectories on flat tables into smooth curves on beautiful surfaces that are well understood by mathematicians. It's a beautiful technique that is worth looking at — you can find out more in this Plus article.
In 2013 the technique helped Ulicigrai to prove a result that came as a shock. Together with the Polish mathematician Krzysztof Fraczek she considered an infinite billiard table containing a lattice of rectangular obstacles. This set-up is known as the Ehrenfest model, after the Russian mathematician Tatyana Ehrenfest and her husband Paul, who studied it to explain the behaviour of molecules in gases.
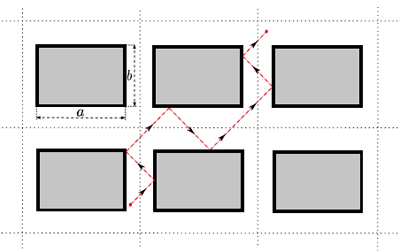
The Ehrenfest model gives an infinite table with an infinite array of rectangular obstacles. Image from this paper by Fraczek and Ulcigrai, used by permission.
Letting infinity enter the picture might seem frightening, but it's something that mathematicians do regularly. And since it's a direct generalisation of the rational polygonal set-up — the obstacles are all bounded by straight lines that meet at right angles — Ulcigrai and Fraczek expected to find that here, too, the vast majority of trajectories should be ergodic. But what they eventually proved was the exact opposite: the vast majority of trajectories are not ergodic. Why this is the case is a mystery. "There are other systems in which there is a clear geometric reason for why trajectories are not ergodic," says Ulcigrai. "If you plot your typical trajectory you can see that they stay in a bounded strip, for example. But in our model, if you plot a trajectory you don't see such a reason. The trajectory looks like it does explore the whole table. But we proved that it doesn't. It's deceiving!"
More research will be needed to get behind this mystery of an infinite table. But even finite billiards still poses questions: what happens if your table is a polygon whose angles are irrational multiples of $\pi$, such as $\sqrt{2}\pi$? The fact is that nobody really knows. The question is still wide open.
About this article

Corinna Ulcigrai is a Reader in Pure Mathematics at the University of Bristol. Corinna was born in Trieste, Italy, in 1980. She obtained her diploma in Mathematics from the Scuola Normale Superiore in Pisa (2002) and defended her PhD in mathematics at Princeton University (2007), under the supervision of Ya. G. Sinai (Abel Prize Winner 2014). Her research is in the area of dynamical systems and ergodic theory. She is one of the few international experts in Teichmüller dynamics in the UK and has studied dynamical and chaotic properties of polygonal billiards and flows on surfaces. Corinna was awarded the European Mathematical Society prize for young mathematicians at the 2012 European Congress of Mathematics and was a recipient of the 2013 Whitehead Prize of the London Mathematical Society. She is married to a mathematician and has a young child.
Marianne Freiberger, Editor of Plus, interviewed Corinna at the British Mathematical Colloquium in London in April 2014.