Maths in a minute: Conditional probability

Suppose I roll a die and ask you to guess the number I roll. What's the chance of you getting it right?

As long as the die is fair, so all numbers are equally likely to be rolled, the probability of you guessing correctly is 1/6. But what if I tell you, before I uncover the result, that the number I have rolled is odd? Then there are only three possible outcomes: 1, 3, and 5. The chance of you guessing correctly is now 1/3. Halving the number of possible outcomes has doubled your chance of getting it right.

What we have been looking at here is a conditional probability: the probability of you guessing correctly given that I told you that I have rolled an odd number.

More generally, given to events $A$ and $B,$ the conditional probability of $B$ occurring given that $A$ has occurred is written as $P(B|A).$ To work it out, you can use the formula $$P(B|A)=\frac{P(A \; and \;B)}{P(A)},$$

where $P(A \; and \;B)$ is the probability of both $A$ and $B$ occurring.

But why is that formula true? We can view the probability of an event as the proportion among all possible outcomes in which the event occurs. In our example, this is why the probability of rolling a $5$ is $1/6$: there are six possible outcomes of which a $5$ is one. This means that the probability $P(A \; and \;B)$ that both $A$ and $B$ occurred is the proportion among all possible outcomes in which both $A$ and $B$ occurred. Now if we're looking for the probability $P(B|A)$ (e.g. the number I rolled is a $5$ given that it's odd) then we're also looking for a proportion among outcomes in which both $A$ and $B$ occurred. However, we're no longer looking for this proportion among the collection of all possible outcomes (e.g. the numbers $1$ to $ 6$), but only among the collection of all outcomes in which $A$ has already occurred (e.g. the numbers $1, 3,$ and $5$). This means that, to get $P(B|A)$, we have to divide the initial probability $P(A \; and \;B)$ by the proportion of outcomes in which $A$ has occurred, which is $P(A)$. So $$P(B|A)=\frac{P(A \; and \;B)}{P(A)},$$

as we claimed above.

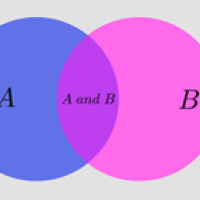
If you prefer some visual intuition, look at the Venn diagram below. The entire rectangle represents all possible outcomes. The left circle represents all the outcomes in which $A$ occurred. The right circle represents all the outcomes in which $B$ occurred. The intersection represents all the outcomes in which both $A$ and $B$ occurred. Let's assume the areas of all the regions shown reflect the probabilities: the area of the entire rectangle is $1$, the area of the circle representing $A$ is $P(A)$, etc. Then the area of the intersection of the two circles is $P(A\; and \; B)$. The conditional probability $P(B|A)$ is the area of the intersection, not as a proportion of the area of the entire rectangle, but as a proportion of the area of the circle representing $A,$ which is $P(A).$ This gives the result.

As a little extra, note that we can rearrange the equation $$P(B|A)=\frac{P(A \; and \;B)}{P(A)},$$

to say $$P(B|A)P(A)=P(A \; and \;B).$$

Noting that $P(A \; and \;B) = P(B \; and \;A),$ we get $$P(A \; and \;B)=P(B|A)P(A)=P(A|B)P(B) = P(B \; and \;A).$$

Rearranging the middle part of this string of equations gives $$P(B|A)=\frac{P(A|B)P(B)}{P(A)}.$$

This is nothing less than the famous Bayes' theorem, which you can read about here.