Friends and strangers

Can we always find order in systems that are disordered? If so, just how large does a system have to be to contain a certain amount of order?

Let's consider a concrete example. Suppose there is a room with six people in it. We are interested in whether people in this room know each other or not. Let's call two people friends if they know each other, strangers if they don't.

Clearly the most orderly case would be if the six are either all friends, or all strangers. Unfortunately the people have been chosen at random, so there will probably be a jumble of friends and strangers in the room. Suppose we draw lines joining every pair of people in the room and colour them blue if the two are friends, red if they are strangers. Then the result might look something like this:

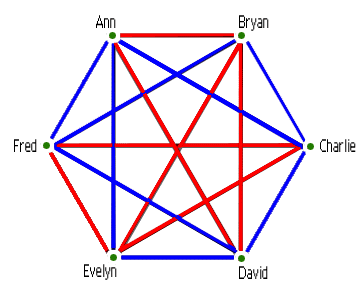
This graph looks pretty chaotic. But we can ask: can we at least find three people in the room who are either all friends (a blue triangle) or all strangers (a red triangle)? In this case the answer is "yes". But what if the original graph had been different? Would we always have been able to find an orderly set of three people?

The answer is yes and one way of proving it would be to list all possible colourings, and check each one in turn. Unfortunately there are over 30,000 of those, so this proof would be more than a little tedious. But there is an easier method. First choose any point in your graph, and note that five lines come out of it - one to each of the other five points:

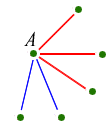
With five lines there must be at least three of one colour. Let's suppose there are three red lines. So we have four points like this:

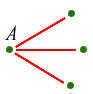
What colours are the three remaining lines? If even one of them is red, then it makes a red triangle together with point A (left). And if not, the three together make a blue triangle (right):

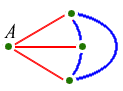We've proved that with six points (or more, of course), there must be three friends or three strangers. This suggests the question, "How many people do we need, to be sure of finding either three friends, or three strangers?" This is our first example of a Ramsey number, and is written as R(3,3). It is named after the mathematician Frank Ramsey who was working in the 1920s. We've seen that six people is certainly enough; in other words, R(3,3) isn't any larger than 6. But would five points have been enough? The graph below with five points shows that the answer is no:

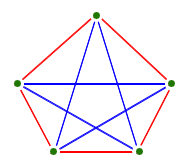
So we have proved that R(3,3)=6. With a bit of work you can show that R(4,4)=18. What about R(a,b) for general values of a and b? Can we be sure it even exists? Perhaps no number of people is enough to guarantee a friends and b strangers. But luckily we can be sure — this result is known as Ramsey's theorem. It tells us that however much orderliness we want, we can find it as long as the graph we are given is big enough.

So what is the value of R(5,5)? The answer is: nobody knows! Very few Ramsey numbers R(a,b) are actually known (with a and b both bigger than 2). The most we can say about R(5,5) with our present knowledge is that it is somewhere between 42 and 49.

How can it be so difficult to get an accurate value? Arguments involve finding upper bounds — for example, we saw quite easily that R(3,3) could not be bigger than 6. But to show that it could not be as small as 5, we had to construct a graph with 5 points, as a counterexample. The problem is that we are looking for examples of order, so the best counterexamples will usually have lots of disorder — they will look random. This makes it hard or impossible to find a "rule" that gives good counterexamples. Anything constructed by rule will probably have too much order in it.

Also, our upper bounds may be too high, but how will we ever prove it? Perhaps by examining all possible graphs on a computer to show that one has the right number of friends or strangers? The problem with this approach is that numbers explode rapidly. To show that R(5,5) is at most 49 we would have to look at 2¹¹⁷⁶ possible colourings of a graph. This number is far, far bigger than the number of particles in the known Universe. So there is no chance of even the fastest computer imaginable ever finishing such a search. This is a puzzle we may never know the answer to.

This is an edited version Imre Leader's article Friends and strangers. You can read the full article here.