
Maths in a minute: Euler's identity
Euler's identity is often hailed as the most beautiful formula in mathematics. People wear it on T-shirts and get it tattooed on their bodies. Why?
The identity reads $$e^{i\pi}+1=0,$$
Leonhard Euler, 1707-1783. Portrait by Johann Georg Brucker.
But where does it come from and what does it mean? As we mentioned above, $i =\sqrt{-1}$. This might seem shocking because negative numbers are not supposed to have square roots. However, if we simply decree that $-1$ does have a square root and call it $i$, then we can build a whole new class of numbers, called the complex numbers. Complex numbers have the form $x+iy,$ where $x$ and $y$ are ordinary real numbers (for the complex number $i$ we have $x=0$ and $y=1$). See here for a quick introduction to complex numbers and how to calculate with them. Note that a real number can also be viewed as a complex number. The number $-1$, for example, is a complex number with $x=-1$ and $y=0$.
Just like a real number is represented by a point on a number line, a complex number $z$ is represented by a point on the plane. To the complex number $z=x+iy$ we associate the point with coordinates $(x,y)$.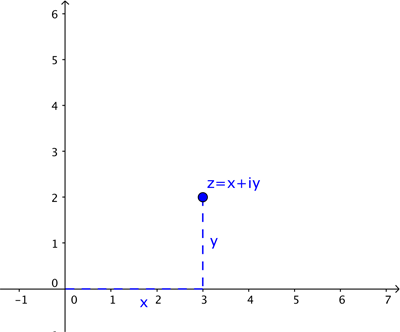
In this description we used Cartesian coordinates: they describe the location of a point by telling you how far to walk along the horizontal direction and how far to walk along the vertical direction. Sometimes, however, it's more convenient to describe the location of a point in terms of the arrow starting at the crossing point of the two axes as shown below.
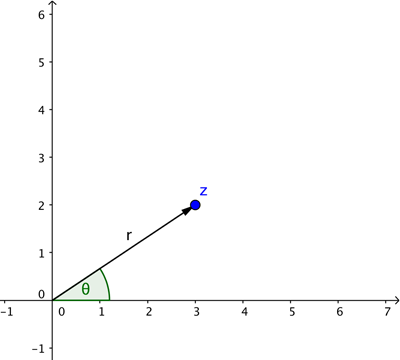
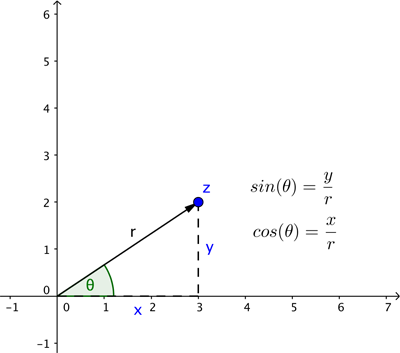
You can prove this using power series, see here to find out more. It's a beautiful fact that the exponential function and the two trigonometric functions sine and cosine are linked in this way. And it means that any complex number $z$ can be written as $re^{i\theta}$ where $r$ is the length of the line connecting the point on the plane that is associated to $z$ to the crossing point of the axes, and $\theta$ is the angle that line makes with the positive $x$-axis (measured anti-clockwise).
This now makes Euler's identity crystal clear. The complex number $e^{i\pi} = 1 \times e^{i\pi}$ represents the point on the plane at distance $1$ from the crossing point of the axes with an associated angle of $\pi$. That's the point with Cartesian coordinates $(-1,0)$ which represents the complex number $-1$.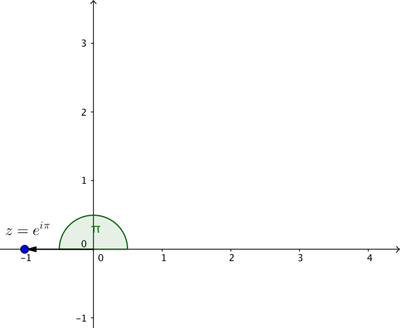
Comments
Adewunmi Fareo
Beautifully written. Even a lay man will understand
Robin
This is beautiful indeed, but for the every man and every woman, it could use a more robust explanation of the significance of e.
Tavio D'Angelis
If I ask whether one real number a is greater than one real number b, I can imagine 'walking' along the real number line from a to b and determining whether i am walking to the left or to the right, intuitively:
if a-b>0 then a>b else a
warren wolfe
No, they can't. You can order their magnitudes, real parts, imaginary parts and angles, but you can't order the numbers themselves. For example, is 3 + 4i greater than equal to or less than 4 + 3i?
Chris G
I think I found an interesting fact about e independently, which of course doesn't make it a new discovery.
I was looking at self roots, that is numbers that are the nth root of n. 1 root 1 = 1, 2 root 2 = 1.4142..., 3 root 3 = 1.4422. 4 root 4 = 1.4142..., 5 root 5 = 1.3797..., 6 root 6 = 1.3480, 100 root 100 = 1.0471..., 1000 root 1000 = 1.0069...
At first the values in the list increase from 1 to a maximum with 3 root 3, then appear to converge on 1 again. But while 3 may have the biggest self root of any integer at 1.4422, a smaller number, 2.7, has an even bigger one at 1.444655705... But e root e rises to 1.444667861..., while 2.718981828 root 2.71898828 (which is just 0.0007 bigger than e) declines again to 1.444667843...
So e has the biggest self root of any number.
(Another interesting fact to emerge is that 2 root 2 = 4 root 4, are they the only two equal self roots?)
Please tell me where I can find this in the literature.
Ahmad Mahmood Qureshi
Check the function y=x^(1/x) for extreme values!
The function has a maximum at x=e.
Ron Duggleby
I'm not much of a mathematician but it seems to be wrong.
Here is my logic:
e^(i x Pi) = -1
Squaring:
e^(2 x i x Pi) = 1
Take natural logs:
2 x i x Pi = 0
Square it:
-4 x Pi x Pi = 0
Therefore:
-39.4784176 ... = 0
I don't see where I have gone wrong, but I'm sure it must be totally elementary.
x
you didnt square the LHS correctly. ( e^(i x pi) )^2