
Does it pay to be nice? – the maths of altruism part i
Does it pay to be nice? Yes, it does. And we're not just talking about that warm fuzzy feeling inside, it pays in evolutionary terms of genetic success too. In fact being nice is unavoidable; humans, or any population of interacting individuals (including animals, insects, cells and even molecules) will inevitably cooperate with each other.
It took cooperation to get from single-celled to multicellular organisms, such as the nematode C. elegans (stained to highlight the nuclei of all cells.) (Image from PLos Biology)
Professor Martin Nowak, from the Program for Evolutionary Dynamics at Harvard University, sees cooperation everywhere. So much so, that he believes cooperation is the third process necessary for evolution, after mutation and natural selection: "You might say that whenever evolution wants to come up with some creative new solution, such as the emergence of the first cell, going from single-celled organisms to multicellular organisms, or the emergence of insect societies or human societies, cooperation plays a role."
Over the last 30 years Nowak and his colleagues have created and investigated a series of evolutionary games, each based on how populations interact in the real world. To his surprise, cooperation has emerged as the most successful behaviour in game after game. And this isn't a question of moral judgment, this is all judged in the cold hard terms of the mathematics of evolution.
Book-keeping…
Using mathematics to describe a human behaviour, such as cooperation, might at first seem quite absurd. But it is possible thanks to the convergence of two very important areas of mathematics.
The first of these is the mathematics of evolution. Charles Darwin expressed his theory of evolution in words when it was first published in 1859, and for many years this revolutionary theory could only be discussed verbally. Today evolutionary theory has a strong mathematical basis. "Just talking about evolution wouldn't be using the level of precision that is actually available," says Nowak. "It would be like physicists talking about the Solar System only in words and not using the equations of Newton or Einstein."
"Evolution is very precise and every idea needs to be couched in this language of the mathematics of evolution," says Nowak. The maths you need is a bit like book-keeping, describing how different strategies, different mutants, reproduce in a population and keeping track of who will be abundant and at what time.
…and playing games
Nowak's work is also based on game theory. This area of mathematics, founded by mathematician John von Neumann and economist Oskar Morgenstern in the 1940s, revolutionised economics by making it possible to describe and understand the strategies people used when making decisions in a competitive environment.
Typically in game theory you would consider a game with two players, say you and I, where the outcome (in terms of a cost or benefit) of the game for me would depend on your decision as well as my own (and visa versa). This approach differed from previous economic theories in that it was the interaction of the two parties that was vital; the outcome for each party could not be considered in isolation. "So it's not just an optimisation problem for me and it's not just an optimisation problem for you," says Nowak.
Suppose we are playing a two player game where we each have to simultaneously choose between two choices: to cooperate or not to cooperate (not cooperating is known as defecting). Then the possible outcomes are: we both defect, I defect while you cooperate, I cooperate while you defect, or we both cooperate. You can define the payoffs and costs to each of us for each of these outcomes in a payoff matrix that completely describes the game.
| You cooperate | You defect | |
| I cooperate | -2,-2 | -4,-1 |
| I defect | -1,-4 | -3,-3 |
The values of the payoff matrix, where the first number in each pair is the benefit/cost to me and the second is the benefit/cost to you, can determine lots of different situations.
Direct reciprocity
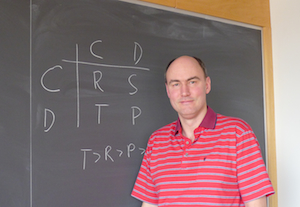
Martin Nowak and the Prisoner's Dilemma
The hardest situation to resolve in game theory is known as the Prisoner's Dilemma. (The payoff matrix above gives one example, and the more general form is given in the matrix shown in the photo on the left.) In the Prisoner's Dilemma, if you defect then the best choice for me is to also defect, and if you cooperate the best choice for me is still to defect: either way the logical thing for me is to defect. You will come to the identical conclusion, and so, we will inevitably both defect. It seems irrational to choose to cooperate despite the fact that we both would have had a much better outcome if we had cooperated. This paradoxical outcome lies at the heart of the Prisoner's Dilemma. (You can read more about the prisoner’s dilemma on Plus.)
The Prisoner's Dilemma seems to leave no hope for cooperation if the players act rationally. But surprisingly, in certain situations, cooperation can triumph. "Cooperation doesn't emerge in the Prisoner’s Dilemma unless you have some mechanism in place," says Nowak. The simplest mechanism that allows this is called direct reciprocity.
In a direct reciprocity game we are now no longer playing the Prisoner's Dilemma only once. Instead we will keep playing, deciding if the current round will be the last with some probability. For example, we could roll a dice and if it is even then we will play another game. (If you knew that this round was definitely the last it is logical to treat it as a one-off game, leading you to defect. The same argument then works for the previous round, and the previous round, resulting in you always defecting as you would in a single play game.)
The defining feature of a direct reciprocity game is that our strategies will depend on the past history of our opponent's behaviour:
If I cooperated last time, you will cooperate this time with probability p.
If I defected last time, you will cooperate this time with probability q.
"So your strategy doesn't depend on what you did, it just reacts to what I did," says Nowak, "and it is completely defined by just two parameters: p and q."

Stickleback fish rely on the Tit-for-tat strategy when approaching a potential predator to determine how dangerous it is. As pair of stickleback approach in short spurts, each spurt can be thought of as a round of the Prisoner's Dilemma. (Image by Ron Offermans)
The political scientist Robert Axelrod explored this iterative version of the Prisoner's Dilemma in the 1970s. Instead of just having the game between two players, Axelrod invited people to submit strategies that would all compete as players in a tournament. Each player (representing one of the submitted strategies) would play every other player in each round and the winning strategy would be the one with the highest payoff at the end of the tournament.
"The undisputed champion in this [tournament] was Tit-for-tat", says Nowak. If you play this strategy then at our first meeting you will always cooperate. Thereafter you will repeat my last move: cooperating if I cooperated in our last game and defecting if I defected in our last game. This eye for an eye strategy is described by p=1 and q=0.
In the 1980s, Nowak and Karl Sigmund (his PhD supervisor at the University of Vienna) explored what happened in these tournaments when some important ideas from evolution were introduced. The first of these was mutation: "The old tournaments had these artificial strategies, rather than allowing natural selection to generate strategies by random mutation." Instead Nowak started off with a random distribution of strategies, choosing the values of p and q for each initial strategy at random. Then the payoff in each round could be thought of as reproductive success – the more successful a player was the more offspring they produced to play the next round. And the strategy of each of these offspring would be based on their parent's strategy, but allowing for some random mutations in the values of p and q.
The other problem Nowak identified was that the tournaments didn't allow for any errors to occur. Errors come in two flavours, says Nowak, trembling hand – where you mean to do one thing and accidentally do something else – and fuzzy mind – where you incorrectly remember the past. "Fuzzy minds leads to the scenario where you and I have different interpretations of history. That's a typical feature of human interaction where there are two parties in conflict and both know, for sure, that the other one started it!" Nowak introduced the possibility of errors into his tournament by giving each player a probability that they would make these errors.
The history of human conflict?
Nowak set his evolutionary mathematical model of the repeated Prisoner's Dilemma to run on his computer and sat back to watch what would happen. "The first thing we saw was the emergence of Always Defect: no matter what you do I'll always defect." It is intuitively obvious that the defectors were the early victors in a game starting from a population of random strategies: if they are going to play randomly it is always better for you to defect.
The defectors were not on top for long. Very suddenly the population swung over from Always Defect to Tit-for-tat, the winning strategy in Axelrod’s original tournaments. But most interestingly it didn't end there; Tit-for-tat didn't last for long, just 10 or 20 or so generations. "Tit-for-tat was just like a catalyst, speeding up a chemical reaction but disappearing immediately after," says Nowak.

Evolutionary mathematics can explain the cycles of war and peace in human history. (Engraving by Hans Holbein the Younger)
What remained was Generous Tit-for-tat, a more cooperative strategy that incorporated an idea of forgiveness. "In this strategy if you cooperated last time then I will definitely cooperate this time, so p=1. And if you defected last time I will still cooperate with a certain probability. So I will always cooperate if you cooperate, and I sometimes cooperate even if you defect, and that is forgiveness." This probability of forgiveness was just the probability q in each strategy. The most successful strategy to emerge from the tournament had p=1 and q=1/3.
This was a dramatic difference to Axelrod’s old tournaments where Tit-for-tat reigned supreme. Even more surprising was that the system carried on evolving, the society becoming more and more cooperative, more and more lenient, until it was dominated by players who always cooperated. "And once you have a society of Always Cooperate it invites the invasion of Always Defect," says Nowak. All it takes is a few mutations in the strategies as they reproduce and the whole cycle will start again.
"It is very beautiful because you have these cycles of cooperation and defection." Nowak's first observations in the field have since been confirmed by many other studies over the years: cooperation is never fully stable. "So we have a simple mathematical version of oscillations in human history, where you have cooperation for some time, then it is destroyed, then it is rebuilt, and so on."
You can read more about the rise of cooperation in other situations in second part of this article, including how evolutionary game theory might just save the world...
About this article

Martin Nowak and his colleagues at the Program for Evolutionary Dynamics
Martin Nowak is Professor of Biology and of Mathematics at Harvard University and Director of Harvard’s Program for Evolutionary Dynamics. You can read a review on Plus of Nowak's latest book, SuperCooperators, written with Roger Highfield.
Rachel Thomas, editor of Plus, interviewed Martin Nowak in Boston in January 2012.
Comments
Anonymous
I didn't realise that all mathematicians had evolved poor eyesight:-)
Anonymous
Do these guys have a group discount at LensCrafters?
Anonymous
If, for example, I was in an ongoing dispute with a troublesome, anti-social neighbour, where it is best if we both cooperate:
would this be a valid matrix? -
I assign points as follows.
I cooperate: +1 for him
I defect: -1 for him
He cooperates: +1 for me
He defects: -1 for me
number pairs in this form: me/him
He cooperates He defects
I cooperate +1/+1 -1/+1
I defect +1/-1 -1/-1
which would make, if we wish:
TOTALS
He cooperates He defects
I cooperate 2 0
I defect 0 -2
What do you think? I would value a mathematician's opinion.
Thank you,
Simon Perry.
Damon Burro
I lost my bookmark and it took me a few months to find it. Question, if it be so allowed -- how might you apply this to politics? Seems relevant "today".