Seeing proof
A while ago John Diamantopoulos sent us some beautiful visual proofs of Pythagoras' theorem. He has now been in touch again with visual proofs of two well-known algebraic identities. The first one is
$$(a+b)^2=a^2+2ab+b^2.$$You can see that this is true in John's Geogebra applet below: the square with side length $a+b$ divides up in exactly the right way. You can use your mouse to move the point $P$ to see that this works for any ratio of $a$ and $b$. Since the picture can be scaled to any size, this means it works for all values of $a$ and $b$.
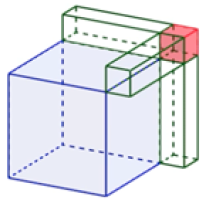
The second identity is $$(a+b)^3 = a^3+3ab^2+3ba^2+b^3.$$
To see why this is true geometrically we need to use cubes, rather than squares. Again, it turns out that a cube with side length $a+b$ divides up in exactly the right way. We have made a movie to illustrate this.
In the Geogebra applet below, use the slider on the left to adjust the ratio between $a$ and $b$ and see that the proof does indeed work for all ratios. By clicking and dragging the background you can also rotate the cube. Enjoy!
About this article

John C. D. Diamantopoulos is a Professor in the Department of Mathematics and Computer Science at Northeastern State University in Tahlequah, Oklahoma. His mathematical interests include ordinary differential equations, mathematics education and the history of mathematics. Diamantopoulos is also very active in his church, volunteering on computer productions/presentations and any area that needs attention.
Comments
SANJAY B.KULKARNI
Excellent efforts
duybao20
Easy to understand!