
Brief summary
This article explains how to use Bayes' theorem to update a prediction you have made about a particular process in the light of new information. It uses the example of a coin flip: what's the chance of a coin coming up heads, given it has come up heads on the last 10 flips? This is an example of Bayesian inference, which is crucial in science.
Here is a question for you:
I toss a coin ten times and observe that it comes down heads every time. If I toss it again, what is the chance that it will come down heads?
I have often posed this question to students (at school and university) and also to their teachers. The answer of a mathematically trained student (and usually their teacher), is nearly always the same. They say that the chance of the coin coming down heads on the next throw is exactly 1/2. They can be very adamant about this, and usually tell me that the coin has no memory, or something similar.
If you ask a (less well trained) gambler, then they might say that as the coin has come down heads a lot, it is the turn of tails to come up, so the chance of heads is something less than 1/2.
But, in my opinion (and yes this does lead to some quite heated arguments) both are wrong. In fact the chance of it coming down heads on the next throw is very close to 1. Yes one. How can this be you say, is everything I have been taught wrong? However, for the coin to have a probability of 1/2 of coming down heads on the next throw it must be a fair coin (one with equal likelihood of coming down heads or tails on each throw). Nowhere have I said that the coin is a fair one. You have simply made that assumption.
You have made the assumption in the face of overwhelming evidence to the contrary. If a coin comes down heads every time for ten throws then it is very likely not to be fair. In fact, if the coin is fair, the chance of this happening is $(1/2)^{10}$, which is $1/1024$ (or close to one in a thousand). So you will have to toss a coin ten times, for a thousand different times — that's 10,000 tosses, which I reckon takes at least three hours, to have a fair chance of seeing ten heads.

Most of you will have given up long before then. So it is very reasonable to assume that as we have seen ten heads in a row that something is wrong with the coin, and it is biased in some way to come down heads. Having realised this, it is clear that the chance of it coming down heads on the next throw is going to be much higher than 1/2. But how much higher?
What I am describing here is the way that science works. Suppose that we have some system that we want to investigate. We make a series of observations and from them have to infer what is going on. This involves making hypotheses and then testing those hypotheses against data. Once we have a hypothesis we can start to make predictions. But this can only happen after we have gathered the data, and we must be very careful not to make unrealistic assumptions about the system in the first place.
This is true of our coin, but also of predicting the weather, trying to work out what is going to happen to our climate, and of decision making in response to COVID-19. It also applies to many other aspects of life, from the judicial system to the way that we make policy (and even social) decisions.
Fortunately we have a very powerful tool to help us, it is called Bayesian inference, and it lies at the heart of the meteoric rise that we are seeing in artificial intelligence, machine learning, and the ability of machines to make decisions.
Heads Bayes wins
A criticism that teachers (and students) sometimes make of my first question is that it is too vague. Not enough information is given in the question to give an answer. Certainly this would never pass muster as an exam question, at least for a mathematics exam. In a sense this is correct, but in reality this is the situation we often find ourselves in in real life, where we are forced to make reasonable assumptions to proceed. So, to make the question more precise I will pose it as follows:
I have a bag containing a lot of coins. Most of these are fair coins, with a chance 1/2 of landing on a head or a tail. However, a proportion $p$ (assumed to be small) of the coins are biased and have heads on both sides. If I throw one of these then it will come down heads with a probability of 1 (I am assuming that no coin lands on its side). I pick a coin at random from this bag and throw it 10 times and it comes down heads every time. What is the chance it will come down heads again?

Meteorology relies on Bayesian inference.
In this more precise situation we can almost assume that if the coin has come down heads each time then it is highly likely to be one that is biased. In this case it will come down heads next throw for sure. Using the wonderful method of Bayesian inference we can make this statement much more precise, and even see how it depends on the size of $p.$
To do this we need to consider the idea of the \emph{conditional probability} of an event. In our game above we have a number of possible events. One is the event of choosing a biased coin. Let's write $A$ for this event, and $P(A)$ for the probability of it occurring. Let's write $B$ for the event of choosing a fair coin, so $P(B)$ denotes the probability of this event occurring. Then: $$P(A) = p \;\;\; \mbox{and} \;\;\; P(B) = 1-p.$$
We often call this sort of probability \emph{prior information}. $P(A) = p$ only if I know nothing else about the coin. It is the chance of it being biased, prior to measuring any data.
As soon as we start tossing the coin we learn more about it and we modify our prior information to give what is called a-posteriori knowledge about the system. As human beings our brains do this all the time, as we gather sensory information about our environment, and start to form a picture about what is going on. This is also the process of how a machine learns and updates the knowledge it has about a system. The key tool for such machines is Bayesian analysis, so let's now see how this works.
Suppose that we have events $A$ and $B.$ The \emph{conditional probability} $P(A|B)$ is the probability of event $A$ happening given that event $B$ has happened already.
For example, suppose that $A$ is the event that a coin tossed 10 times will come down heads each time, $B$ is the event that we choose a coin with two heads, and $C$ is the event that we choose a coin which is fair. A little thought shows that $$P(A|B) = 1.$$
This is because the coin has two heads so it has to come down heads every time. Also, we have that $$P(A|C) = 1/1024,$$
as we already worked out above. You can see that $P(A|B)$ is much larger than $P(A|C).$
What Bayes says
There is a general formula relating to conditional probabilities. Writing $P(A\;\mbox{and}\;B)$ for the probability that both $A$ and $B$ occur, the formula is $$P(A\;\mbox{and}\;B) = P(A) P(B|A)$$
This may not be immediately obvious — to see why it is true, see this article.
But, $P(A\;\mbox{and}\;B)$ is the same as $P(B\;\mbox{and}\;A)$, which (by the formula above) is equal to $P(B)P(A|B).$ This means that $$P(A\;\mbox{and}\;B) = P(A) P(B|A) = P(B) P(A|B) = P(B\;\mbox{and}\;A). $$
Reordering this gives $$P(B|A) = \frac{P(A|B)P(B)}{P(A)}. $$
This result is called Bayes' theorem. It was discovered by Revd. Thomas Bayes in 1763 and was published by the Royal Society as An Essay towards solving a Problem in the Doctrine of Chances.

Thomas Bayes (1701-1761)
Bayes was not quite a professional mathematician although he had strong interests in philosophy and statistics. In fact he was a clergyman. But Bayes' theorem is one of the most important results in the whole of mathematics! It is central to probability, statistics, and has countless applications in such diverse fields as tracking satellites (or almost anything else), archaeology, the justice system, meteorology, and even the (notorious) Monty Hall problem. It is also the bedrock on which the whole of machine learning is built. Not bad for one theorem.
We can explain the importance of the theorem in words. Suppose it is event $B$ that we are interested in, and event $A$ is the experiment that we do to try to learn more about $B.$ $P(B)$ is the prior knowledge of event $B$ before we do the experiment. $P(B|A)$ is the a-posteriori knowledge of $B$ after the experiment. Bayes' theorem gives us a way of going from the prior to the a-posteriori knowledge. We have managed to infer what is happening from the data, hence the phrase Bayesian inference. This idea is used over and over again in all aspects of science when we want to find out what is going on inside a system which we cannot measure directly, and when we have to infer what it is doing from indirect measurements.
What's the chance the coin is biased?
As an example, let's now apply this theorem to our original problem to infer whether the coin has two heads without looking at the coin directly. Again we will say that $A$ is the event that we toss 10 heads in a row, and $B$ is the event that we choose a coin with two heads.
We already know that $P(A|B) = 1,$ and also $P(B) = p.$ So to work out $P(B|A)$ (that is the probability of the coin having two heads given that we have thrown 10 heads in a row) we need to work out $P(A),$ which is the probability that a random coin from the bag, when thrown, comes down heads 10 times. There are two mutually exclusive cases to consider. The first is that we choose a biased coin and then toss ten heads. The probability of this is just the probability $P(B)$ of choosing a biased coin (because once you do that the ten heads are guaranteed). The second case is that we choose and unbiased coin (we write $C$ for this event) and then toss ten heads. The probability of tossing heads ten times in this case is the product of the individual probabilities $P(A|C)P(C).$ The overall probability $P(A)$ of tossing ten heads is now the sum of these two mutually exclusive cases: $$P(A) = P(B) + P(A|C) P(C).$$
We have already worked out all of the terms here: $P(B) = p,$ $P(A|C) = 1/1024$ and $P(C) = 1-p.$ Therefore $$P(A) = p + \frac{(1-p)}{1024.}$$
We can now finish off the calculation to give the probability of the coin being biased given that it has come down heads 10 times. It is $$P(B|A) = \frac{P(A|B)P(B)}{P(A)} = \frac{p}{p + (1-p)/1024}.$$
To give an idea of the size of this, suppose that we have a bag with 100 balls in it, only one of which is biased. Then $p = 1/100.$ The chance of our coin being biased given that it has come down heads 10 times is then $$ P(B|A) = \frac{1/100 }{ 1/100 + \frac{99/100}{1024}} = \frac{1}{(1 + 99/1024)} = 0.9118,$$
so there is a 91\% probability that the coin is biased. Good enough odds for most people. See how the prior probability of 1\% of the coin being biased is changed to 91\% by the application of Bayes' theorem.
What's the chance of heads?
We can now go on to answer the question originally set. What is the chance of a head on the next throw, given that we have already had ten heads?
If the coin is biased (so that's event $B$) then the probability of heads coming up at the next toss is 1. The probability of heads coming up \emph{and} the coin being biased, given the data, is therefore $$1 \times P(B|A).$$
If the coin is not biased (so that's event $C$) then the probability of heads coming up at the next toss is 1/2. The probability of heads coming up \emph{and} the coin being unbiased, given the data, is therefore $$1/2 \times P(C|A).$$
The overall probability of heads coming up again at the eleventh toss of the coin is the sum of the probabilities for the two mutually exclusive events above: $$P(B|A)+1/2P(C|A).$$
We have already worked out $P(B|A)$ and $P(C|A)$ is simply $1-P(B|A)$. Therefore, the probability of heads coming up again is $$P(\mbox{heads again})=\frac{p}{p + (1-p)/1024}+\frac{1}{2}\left(1-\frac{p}{p + (1-p)/1024}\right) = \frac{2048p+(1-p)}{2048p+2(1-p)}.
If $p = 1/100$ then $P(\mbox{heads again}) = 0.955$ or nearly 96\%. Close enough to 1 for government work.
In the graph below we plot $P(\mbox{heads again})$ as a function of $p$. You can see that $p$ has to be really small before $P(\mbox{heads again})$ is appreciably different from 1. So we are justified in saying that the answer to the original question is that the chance of a head is very close to 1, even if we don't really know the value of $p$.
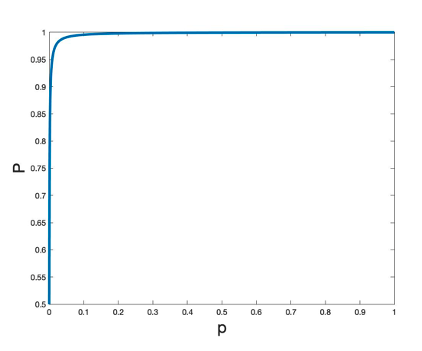
The probability P(heads again) plotted against p.
Job done...
...unless, that is, I have been lying to you about the data. To find out what to do in that case, and what it has to do with weather forecasting and even machine learning, see the next article.
About this article

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath and part of Maths4DL, a joint research programme of the Universities of Bath and Cambridge and University College London, which explores the mathematics of deep learning. Chris is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
Chris has written the popular maths book Climate, Chaos and COVID, published by World Scientific, and co-written the popular mathematics books Mathematics Galore!, published by Oxford University Press, with C. Sangwin. Chris features in the book 50 Visions of Mathematics ed. Sam Parc.
This content is part of our collaboration with the Mathematics for Deep Learning (Maths4DL) research programme, which brings together researchers from the universities of Bath and Cambridge, and University College London. Maths4DL aims to combine theory, modelling, data and computation to unlock the next generation of deep learning. You can see more content produced with Maths4DL here.
