Henry Perigal 1801 - 1898

It is essential to true history that the minor and secondary phenomena of the progress of mind should be more carefully examined ...

Augustus De Morgan, in the Introduction to Arithmetical Books

Henry Perigal was an amateur mathematician whose life spanned almost the entire nineteenth century and who is now known principally for an elegant cut-and-shift proof - what is now called a dissection proof - of Pythagoras' Theorem. He himself perhaps felt that this was his most important accomplishment - his diagram was carved, presumably at his own request, on his gravestone (right).

He discovered a number of other interesting geometrical dissections, however, and both his life and his role in nineteenth century British scientific society are curious.

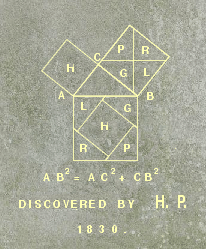
Perigal's diagram

The diagram on the south side of Perigal's tomb.

The diagram redrawn.

Pythagoras' Theorem asserts that for a right-angled triangle, the area of the square on the hypotenuse (the longest side) is the sum of the areas of the squares on the smaller sides. Many people are familiar with at least one proof or another. Those which people often remember best, because the basic reasoning is most direct, are dissection proofs, which cut the larger square up into regions which can be reassembled to make up the smaller squares. The diagram on Perigal's gravestone illustrates a dissection proof apparently discovered by Perigal himself. It is distinguished mostly by its pleasing symmetry.

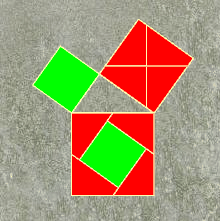Perigal's proof shows that the larger square can be cut up and reassembled to make up the smaller ones. It is not so easy to see exactly why this is so.

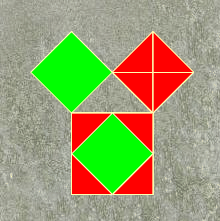Perigal's dissection when two sides are equal. In this case it is not difficult to show that the two green squares and all the red triangles are congruent.

It is not easy to justify Perigal's dissection in general (as will be done later on). But there is one case where it is easy to do so, and that is where the two smaller sides of the triangle are equal (and the ratio of the hypotenuse to side is 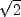). This is the case apparently pictured on Babylonian tablets dating to about 1600 B.C. (thus among the earliest examples of geometrical diagrams known, and perhaps the earliest extant examples of mathematical reasoning). It is also that discussed by Plato in the dialogue Meno.

His life

Henry Perigal was born on April 1(!), 1801, and died in June of 1898. His family was long-lived - he was known as Henry Perigal, junior, until he was 66, because his father lived to be 100. We know much more about him than we would normally because soon after his death his brother Frederick (10 years younger than Henry) collected together a few of his own remarks as well as excerpts from the writings of Henry and others, and published these in a short memoir of limited distribution.

A photograph of Henry Perigal (who was once called "the venerable patriarch of the London scientific societies") towards the end of his life, from the frontispiece of his brother's memoir.

It seems that his family was genteel but poor. He worked at odd jobs for many years, but finally in his mid forties he became a book keeper for a stock broker friend of his, and remained in this position until his retirement at 87 - in order, he said, to devote more time to scientific pursuits. He pursued science throughout his life, but with mixed success. He was, to use the word coined by Augustus De Morgan, a paradoxer - what we would call a crank. By his own account he came across his proof of Pythagoras' Theorem while trying to square the circle, and he held probably throughout all his life the somewhat bizarre belief that in moving around the Earth so as to present constantly the same face to us, the moon did not rotate relative to the stars. A possibly related unorthodox belief of his is suggested by his diary entry:

1884, May 7 - to the Gresham Lecture on Astronomy, by Ledger; explained to the lecturer Foucault's pendulum delusion.

It is hard to know what he meant by his somewhat obstinately held views on rotation. He was by no means a novice in understanding the nature of rotation. His father was a good friend of John Ibbetson, reasonably well known even today for having invented and written about a tool used in ornamental wood turning called the geometric chuck. Henry Perigal himself became an expert in the use of the geometric chuck, and used it to produce a huge number of wood engravings, many of them well known to scientists of his era. In one of his articles written for the Athenaeum (later bound into A Budget of Paradoxes) Augustus De Morgan writes in a review of one of Perigal's publications that tries to persuade a larger public about the non-rotation of the moon:

Mr. Henry Perigal helped me twenty years ago with the diagrams, direct from the lathe to the wood, for the article "Trochoidal curves," in the Penny Cyclopaedia: these cuts add very greatly to the value of the article, which indeed could not have been made intelligible without them. He has had many years' experience as an amateur turner, in combination of double and triple and circular motions, and has published valuable diagrams in profusion ... His familiarity with combined motions enabled him to handle his arguments [about the moon's motion] much better [than another crank] ... But he is as wrong as the rest.

And at the end of the article in the Penny Cyclopaedia De Morgan writes:

... the specimens of curves in this article are all the product of machinery. We are indebted to ... Mr. Henry Perigal ... a gentleman whose pursuits are scientific, and who practices the higher branches of turning as an amateur ... [The curves] given in this article were executed in his lathe by means of Ibbetson's geometric chuck, a contrivance the results of which are well known to turners, but which have never been exhibited, as far as we know, in any article professing to give a mathematical classification of them.

This gives a rare look at details of the production of mathematical drawings (at this time, mostly wood engraving on the endgrain of boxwood) in the nineteenth century. It seems to me likely, for example, that Perigal was himself directly responsible for the illustrations in his own publications.

Augustus De Morgan was not alone in this combination of respect and mild exasperation concerning Henry Perigal. Perigal was friends with at least two of the Royal Astronomers during his life (George Biddell Airy and W. H. M. Christie) in spite of his openly expressed unorthodox views. Those who attended his 95th birthday celebration included Christie, Lord Kelvin, Lord Rayleigh, George Gabriel Stokes, Silvanus P. Thompson, and Vice-Admiral J. P. Maclear (commander of the scientific vessel Challenger during her voyage of 1872-1876). James W. Glaisher, one of the very first mathematicians to make a profession of numerical analysis, was a very close friend but wrote to excuse himself from the party. Perigal's diary records a meeting with the mathematician J. J. Sylvester "on a proposition to assist him in getting a model of a geometric curve." His friends and acquaintances thus include some of the most distinguished in all of British science of his time.

Perigal was a member of many scientific societies, in particular a Fellow of the Royal Astronomical Society, and treasurer of the Royal Meteorological Society for many years. At one scientific meeting his portrait was exhibited with the caption, "Venerable patriarch of the London scientific societies." His brother writes:

Mr. Perigal was desirous of being elected a Fellow of the Royal Society, believing that his investigations in curvilinear motion; his mechanical contrivances; and his services in various branches of science, entitled him to that distinction; but he was aware that his known opinions, respecting certain dogmas relating to Astronomy - not being orthodox - would be likely to militate against his admission; and so it proved when his name was put to the vote (when it is probable that many of his personal friends voted adversely); he was naturally disappointed with the result, but observed that his possessing an open mind in all questions, and not adopting doctrines without his judgment assented thereto, should be a reason in his favor, instead of against him.

Among diary entries made by Henry Perigal and quoted in his brother's memoir we find:

1865, Jan. 13 - Dined with the Astronomical Club; after dinner, the question as to the the moon's rotation was put to the vote, when the numbers were: 10 for Adams and rotation, 11 for Perigal and non-rotation.

I imagine the reference here is to John Couch Adams, one of the two mathematical astronomers responsible earlier in the century for the discovery, on theoretical grounds, of the planet Neptune. One would like very much to have Adams' account of the event.

Why is Perigal's dissection a proof of Pythagoras' Theorem?

It may not be immediately evident from Perigal's own diagram how to carry out the details of a proof. The following pictures should explain how it goes.

1. The construction of the diagram

• Draw the triangle and the squares on its sides (Fig 1).

• Place a cross in the larger square on a side, centred at the centre of that square and aligned horizontally and vertically (Fig 2).

• Cross the square on the hypotenuse starting from halfway along it, running parallel to the short side (Fig 3).

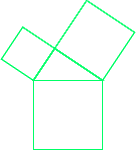Figure 1

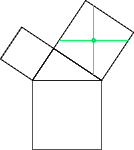Figure 2

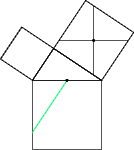Figure 3

• Draw three other similar lines by rotating this one (Fig 4).

• Erase the tips of these lines (Fig 5) ...

• ... to obtain Perigal's figure (Fig 6).

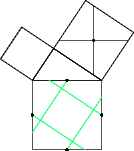Figure 4

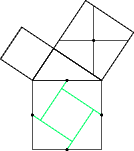Figure 5

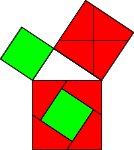Figure 6

2. The quadrilaterals are congruent

It must then be shown that this actually does dissect the larger square into pieces that can be reassembled to make up the smaller ones.

• The shape in Fig 7 above is a parallelogram.

• Because of this and rotational symmetry, all the red segments in Fig 8 have the same length.

• Finally, in Fig 9, all corresponding sides are parallel. This implies that the marked quadrilaterals (and so, by symmetry, all the quadrilaterals) are congruent.

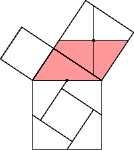Figure 7

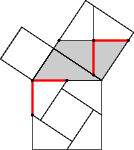Figure 8

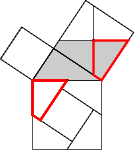Figure 9

3. The squares are congruent

• In Fig 10 the red segments on the left are both equal to the green one on the right, hence equal to each other.

• Subtracting equal segments demonstrates that the squares are equal, as in Fig 11. This finishes the proof.

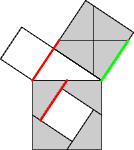Figure 10

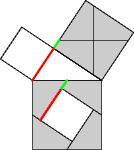Figure 11

A generalization

A few years after Perigal died, it was observed that his proof is only one of an infinite family of similar ones. The way to obtain them starts with a Pythagoras tiling.

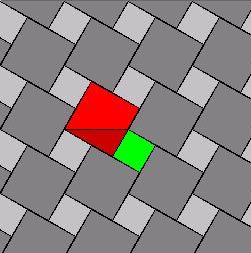
A Pythagoras tiling covers the plane with periodic copies of the squares on the sides of the right triangle.

Then overlay this with a tiling constructed from copies of the square on the hypotenuse. Different dissections correspond to different placements of this second tiling. Perigal's dissection is just one of the possibilities. One advantage of placing Perigal's figure in such a lattice tiling is that it makes checking the validity of his dissection much more transparent. Congruences can be verified by lattice translation.

You can use interactive versions of this figure if you enable Java in your browser and reload this page.

Moving the tiny red control node gives different decompositions of the square on the hypothenuse into pieces which come from the squares on the sides.

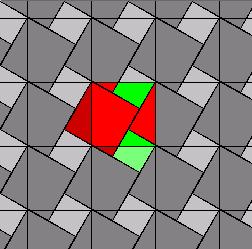
One of the dissections in the family is the one attributed to Thabit Ibn Qurra, a ninth century Arabic mathematician. It has been discovered independently many times.

His grave

Henry Perigal's body was cremated and the ashes buried in the churchyard of the Church of St. Mary and St. Peter in Wennington, Essex (between Rainham and Aveley, just off the A11, about 15 miles east of central London).

The tombstone as it appeared in a photograph in Frederick Perigal's memoir. The dissection diagram is on the invisible face around to the left. The diagram on the right illustrates a fact about parabolas.

The inscription reads:

Sacred to the memory of / HENRY PERIGAL / (Cyclops) / F.R.A.S. F.R.M.S. M.R.I. / 40 years treasurer of Met. S. &c. / Born 1st April 1801. / Died 6th June 1898. / Cremated at Woking / His ashes lie beneath / Descended from a Huguenot family / who escaped from France to England / after the revocation of the / edict of Nantes in 1633.

A learned and ingenious geometrician / he investigated and illustrated / the laws of / compound circular motion.

The bottom layer of text shown in Frederick Perigal's photograph has been buried by drifting soil and obliterated over the years.

Here is more about the Church of St. Mary and St. Peter. Perigal's grave is way off to the right, in the deep shadow of the photograph there. You can use MapQuest to locate Rainham (but if you try for Wennington you'll get the one near Lancaster).

Afterword

Henry Perigal was certainly an obscure figure in nineteenth century English mathematics, entering more or less through the back door. But his work on dissections has not been forgotten. Geometric dissections are even now an active subject, and one almost exclusively the domain of amateur mathematicians. It was only around the turn of the nineteenth century into the twentieth, particularly with Hilbert's work on Euclid's concepts of area and volume, that it played an important role in the main stream of mathematics.

For more information, see the bibliography.

About the author

Bill Casselman does research on automorphic forms and algorithms for Coxeter groups. His principal hobby is the use of images in mathematics, both still and animated, and not too long ago he wrote a review article on the topic: Pictures and proofs, for the Notices of the American Mathematical Society. He is also the technical editor of the collected work of Robert Langlands, which can be found on line at the UBC SunSite.