Physicists everywhere are celebrating the news of the first detection of gravitational waves and the first direct observation of black holes. Both of these were predictions from Einstein's general theory of relativity, confirmed almost exactly 100 years after he published the theory.

An artist's drawing a black hole named Cygnus X-1. It formed when a large star caved in. This black hole pulls matter from blue star beside it. Image: NASA/CXC/M.Weiss.

General relativity changed the way we thought about gravity and the nature of the Universe. Einstein combined space and time into one entity, spacetime, and described gravity as the curvature of spacetime caused by massive objects. To picture this, imagine a large rubber sheet that has been stretched tight – this represents spacetime, the fabric of the Universe. If a bowling ball is placed in the middle the sheet will warp, and any light object nearby, such as a tennis ball, will roll down the curved sheet towards the bowling ball. In an analogous way, spacetime is warped by massive objects and gravity is the result of this curvature. As the famous saying of John Wheeler goes, "spacetime tells matter how to move; matter tells spacetime how to curve." (You can read more about general relativity here.)

Einstein's general theory of relativity describes the mathematical relationship between the curvature of spacetime and the presence of matter, written down as a set of equations. Like the solution to any equation you might have solved at school, a solution to these equations is a set of values for the variables that make the equations true, meaning a Universe with these values would satisfy the mathematical relationships in Einstein's theory. The solution doesn't necessarily have to exist in reality – we'll see an example of this below – but solutions that are compatible with the Universe as we observe it result in predictions such as the gravitational waves and black holes recently observed for the first time.

The first solution to Einstein's equations was found by the physicist and astronomer Karl Schwarzschild in 1915, allegedly while serving in the front in Russia during the World War I. The Schwarzschild solution describes a non-rotating, electrically neutral, and spherically symmetric gravitating body.

It took some time for the physics community to realise that Schwarzschild's solution describes a black hole. Black holes are regions in spacetime from which nothing – not even light – can escape (find out more here). The surface of a black hole is called an event horizon. This horizon is not a physical surface, but marks the boundary of no return – any object that falls through the horizon will never escape the black hole's gravitational field, doomed to hit the black hole singularity, where spacetime curvature becomes unbounded. For a Schwarzschild black hole the event horizon is located at the Schwarzschild radius $r_h$, where $$ r_h=\frac{2GM}{c^2}. $$ Here $M$ is the mass of the black hole, $G$ is Newton's gravitational constant and $c$ is the speed of light. (Physicists often work with slightly different units, so that $G=c=1$ as it makes the maths simpler.)

Growing with time

The larger the surface area, the larger the volume: this is true for ordinary spheres, like the Earth and the Moon. But it's not true for all black holes. Image created by Reto Stöckli, Nazmi El Saleous, and Marit Jentoft-Nilsen, NASA GSFC.

The shape of a Schwarzschild black hole is that of a sphere, and so its area is $A=4\pi r_h^2$. We might be tempted to use our ordinary intuition about geometry, and deduce that the volume of a Schwarzschild black hole must be $V=4/3 \pi r_h^3$. This is, however, not necessarily the case. It turns out that the volume of a black hole is not a well-defined notion in general relativity. The reason is that general relativity is a geometric theory of a four-dimensional spacetime, that is, three dimensions of space and one dimension of time. In order to specify a spatial volume, one has to specify a specific moment in time. However, such a choice is not unique – one of the many counter-intuitive properties of relativity is that different observers have different notions of time. Thus, a black hole can be assigned many different volumes, some more useful than others.

Recently, Marios Christodoulou and Carlo Rovelli showed that it makes sense to talk about the "largest volume" that can be bounded by the event horizon of a Schwarzschild black hole formed by the gravitational collapse of a star. More precisely, they asked: what is the largest spherically symmetric volume that can be bounded by a given black hole's area? They showed that even though a Schwarzschild black hole looks the same forever to an outside observer (ignoring something called Hawking radiation that would shrink the black hole), its volume actually gets larger with time.

When the time $\nu$ is sufficiently large, the volume is given by: $$ V \approx 3\sqrt{3}\pi M^2 \nu . $$ From this expression one sees that the volume of a black hole continues to grow larger and larger, although its surface area never changes! To give an idea of how large the interior of a black hole could become, this formula estimates that the volume for Sagittarius A*, the supermassive black hole at the centre of our Milky Way Galaxy, can fit a million solar systems, despite its Schwarzschild radius being only about 10 times the Earth-Moon distance. (Sagittarius A* is actually a rotating black hole, so its geometry is not really well-described by the Schwarzschild solution, but this subtlety does not change the result by much.)

Growing with dimensions

Our intuition tells us that a larger sphere would contain a larger volume. (In more precise terms, the volume is a monotonically increasing function of surface area.) For example, a sphere of area $A$ has volume that is proportional to $A^{3/2}$, so for larger area the volume is also larger. This is also true for a black hole that is rotating (like the one in the movie Interstellar), as shown by Bengtsson and Jakobsson.

Surprisingly, however, this is not always the case for all black holes. Consider a universe that is filled with a negative cosmological constant $\Lambda$ – the so-called anti-de Sitter space. (You can read more about the cosmological constant here.) A positive cosmological constant is widely thought to be the reason why the expansion of our universe is accelerating: galaxy clusters are moving away from one another at an ever increasing rate (see here). A negative cosmological constant has the opposite effect. That is, a Universe filled with negative $\Lambda$ would eventually collapse.

The acceleration of the expansion of the universe suggests that $\Lambda$ is positive in the real Universe (if indeed $\Lambda$ is the correct explanation of this acceleration; there are various other proposals and models that we will not get into), so we are most probably not living in an anti-de Sitter space. Nevertheless, anti-de Sitter space still plays some important roles in theoretical physics, notably in string theory. So while the black holes described in what follows probably don't exist in the real Universe we inhabit, they are still valid solutions to Einstein's equations describing general relativity.

To topologists a doughnut is equivalent to a tea cup because one can be deformed into the other without tearing.

It turns out that black holes in such a universe (an anti-de Sitter space) need not be spherical, in terms of their topology. Loosely speaking, topology is the shape of a body up to smooth deformation – you can bend and stretch the body and it is topologically the same, as long as you don't rip or cut it. That is to say, if we can smoothly deform one shape into another without tearing or punching a hole into the object, the resulting shape is said to have the same topology as the original shape. For example, a doughnut is topologically equivalent to a tea cup (see here to find out more).

In Einstein's general relativity, the number of spacetime dimensions can be arbitrary. To find black holes that are sufficiently interesting for our purpose, let us consider an anti-de Sitter space with five dimensions, that is, it has four dimensions of space and one dimension of time. A spherical black hole in this universe has a three-dimensional surface "area" and a four-dimensional "volume". It is hard to imagine higher-dimensional objects, however, we can imagine constructing them starting from lower-dimensional objects.

To show how this works, let's consider a usual sphere. (When mathematicians talk about spheres, they mean hollow spheres. A solid one is usually called a ball.) An example of this is the surface of the Earth, which is two-dimensional (called a 2-sphere by mathematicians) since we only need two coordinates (say, longitude and latitude) to specify any point on its surface.

One can construct a 2-sphere starting from a solid circle and gluing up its boundary to a point. (In the language of topology, we identify all the points on the boundary of the circle with a single point on the sphere.)

This process forms a sphere as we normally imagine it, with a two-dimensional surface and a hollow interior. We can use a similar process to make a 3-sphere. Take a solid ball (a sphere with a solid, rather than hollow, interior, like a solid billiard ball) and glue all the points on its surface to a single point, creating a sphere with a 3-dimensional surface. Using a complicated topology that can be obtained from a 3-sphere, we can find a class of black holes where, for two black holes with the same mass, the one that has a larger surface area actually contains a smaller volume, which is totally counter-intuitive.

The topology we need is called the lens space, introduced by the mathematician Heinrich Tietze in 1908. The simplest type of a lens space is constructed as follows. Take a solid ball and divide it in half. Then $p$ points are equally spaced around the equator and we join these points with the north and south poles as shown below, creating $p$ lines of longitude. Now twist the upper hemisphere by $2\pi/p$ radians (recall that a full circle corresponds to $2\pi$ radians, or equivalently, 360 degrees) so that the line on the upper hemisphere now sits above what used to be the next line of longitude on the lower hemisphere. And finally, topologically identify ("glue up") all the upper "triangles" with their corresponding lower partners.

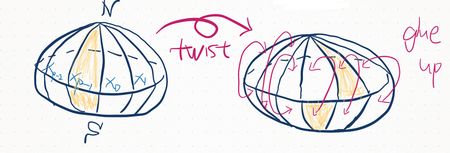
Black holes with three-dimensional horizon with this lens space topology have the peculiar property we mentioned above. For black holes of the same mass, for larger numbers $p$, the horizon area of such a "black lens" decreases, despite its volume increasing.

Appearances can be deceiving

These examples show that, in addition to the surprising property that the largest spherically symmetric volume of a black hole grows with time, in general, the idea that volume of a black hole grows with the size of its surface area is wrong. In other words, by comparing two black holes from the outside, we cannot, in general, infer that the "smaller" black hole contains a lesser amount of volume.

The lesson is that general relativity is a geometric theory in which curvature plays an important role. When calculating the volume of a black hole, the role of geometry and topology is especially evident. Sometimes curved spacetimes and non-trivial topologies can behave very differently from our flat space intuitions. One must, therefore, rely on the rigour of mathematics to guide us in our ongoing quest to understand the Universe.

About the author

This article is based on Yen Chin Ong's academic paper Don't judge a black hole by its area.

A mathematician at heart, Yen Chin Ong is a research fellow at the Nordic Institute for Theoretical Physics (Nordita), which is located in Stockholm, Sweden. He works mainly on general relativity and other modified theories of gravity. His current research focuses on understanding the properties of various black holes.

He has previously taught mathematics at high school, diploma and undergraduate level.