Genetics: Nature's digital code
This article is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below and there is another article based on the talk here.
The phylogenetic tree of life as produced by Ernst Haeckel.
When a green-eyed woman has a child with a blue-eyed man, what colour will the child's eyes be? Well, in all likelihood they won't be turquoise, but either blue or green, or perhaps even brown. This fact gives us a clue as to how nature deals with the genetic information that's passed on from one generation to the next. Nature doesn't work with a continuous spectrum of possibilities, but with separate either/or alternatives. This is similar to how computers transmit the reams of information in the digital world, which is made of the discrete units of 0 and 1. In this article we look at the digital nature of genetic information, and how it appears to be cleverly encoded so that not too many mistakes are made when this information is passed on through the generations.
The colour of peas
The most famous figure in the field of genetics is Charles Darwin, who published his groundbreaking book On the origin of species in 1859. Despite giving an explanation of how species would change and evolve, Darwin was unaware of the mechanism behind this process. The digital nature of genetic information was discovered in 1866 by the monk Gregor Mendel. However, the precise mechanism was only identified a hundred years later with the discovery of the structure of DNA.
Mendel was wondering how phenotypes (or traits) of a species are inherited from one generation to another. An example of such in humans might be eye colour, or height. Mendel instead looked at the colour of peas. He bred successive generations of peas of different colours and made very careful quantitative measurements of what he observed.
In particular he observed that if he took as a parent generation yellow and green peas and crossed them, then all of the next generation were yellow. If he then allowed each plant from the second generation to pollinate itself (peas can do that) he obtained both yellow and green peas in a ratio of 3:1. This already showed a high degree of mathematical regularity. If he then self-pollinated future generations he ended up with a quarter yellow peas, a quarter green peas, and the remaining half a mixture of both yellow and green, again in the 3:1 ratio.

Gregor Mendel.
This was evidence of the discrete nature of inheritance rather than a blending of the yellow and green colours. He explained this by postulating that two factors were responsible for the colour of the pea, a yellow Y factor and a green G factor (today these factors would be called alleles of the same gene). Each plant would have two of these factors (so either YY, YG, GY or GG). A green pea would only arise if there were two G factors. When getting together with another plant to cross-pollinate, a parent plant would pass one of these factors on to its offspring, with each factor having a 50:50 chance of being passed on. A plant getting together with itself to self-pollinate can be regarded as two plants with the same pair of factors cross-pollinating. Mendel started by cross-pollinating yellow plants with the pair of factors YY and green plants with the pair of factors GG.
The second line in the diagram below shows what happens when you combine the first factor from the first parent plant with the first factor from the second parent plant, the first factor from the first plant with the second factor of the second, and so on. It turns out that all offspring plants in this second generation of peas will have the combination YG. The third line shows what combinations of Y and G are possible for the third generation as a result of self-pollination of the second generation. The fourth line shows the combinations that are possible for the fourth generation as a result of self-pollination of the third generation.
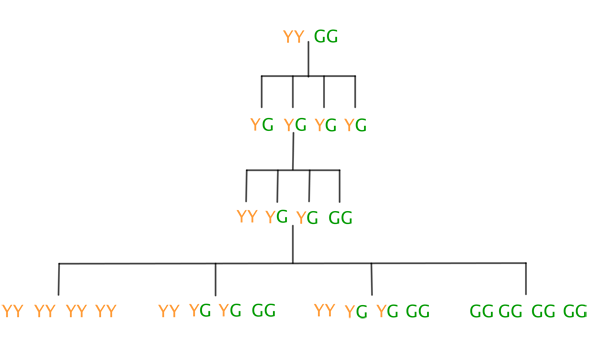
The resulting pea colours are shown below (bear in mind that only GG plants will be green).
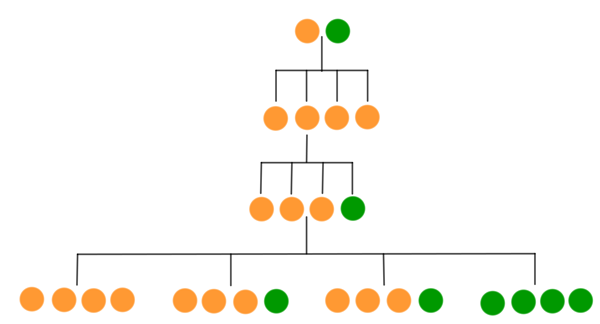
If enough plants are involved in the experiment then we can assume that all of the possible outcomes occur in roughly the proportions given by the diagram: a quarter yellow, a quarter green, and the rest a mixture with a 3:1 ration between yellow and green. These are exactly the proportions Mendel observed.
From peas to us
We now understand the mechanism behind this process: discrete amounts of information are coded in our genes, and the traits of an organism, such as the colour of the peas, depends on the sequence of its genes. The term gene was introduced by Wilhelm Johannsen in 1905. Deoxyribonucleic acid (DNA) was shown to be the molecular repository of genetic information by experiments in the 1940s to 1950s. The structure of DNA was studied using X-ray crystallography by Rosalind Franklin and Maurice Wilkins. This research led James D. Watson and Francis Crick to publish a model of the double-stranded DNA molecule as illustrated below. We can already see a strong mathematical regularity in the shape of this molecule, which begs the question of whether this molecule came into existence at random or through the action of deep mathematical principles.
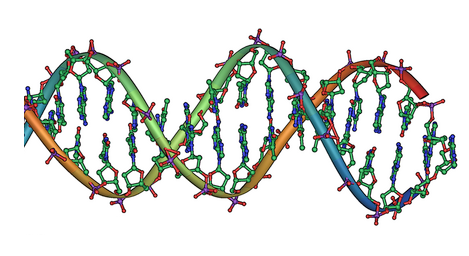
The double helix of DNA.
A gene itself is a sequence of DNA or RNA molecules. A chromosome is a long strand of DNA containing many genes. A human chromosome can have up to 500 million so-called base pairs of DNA with thousands of genes. The DNA is first copied into RNA. The RNA can either itself have a direct function in the body, or, more typically, it provides the template for a protein that then goes on to perform a function.
Because genes are discrete, we can observe a discontinuous inheritance of the traits of an organism. Some genetic traits are easily visible, such as eye colour or height, and some are not, such as blood type, risk for specific diseases, or internal biochemical processes. The total complement of genes in an organism or cell is known as its genome, which may be stored in one or more chromosomes.
The DNA molecule is a chain made from four types of nucleotide units, each composed of a five-carbon sugar, a phosphate group, and one of the four bases: A for adenine, C for cytosine, G for guanine, and T for thymine. The base U for uracil is also present in RNA. The components (base pairs) of the genes act rather like the 0s and 1s of a binary message. As you can see in many other articles on Plus, these binary digits can encode a huge amount of information. Similarly all the proteins in your body are made from protein building blocks called amino acids. There are twenty different amino acids used to make proteins, all of which are specified from a four-letter code sequence made from the letters A, C, G and U.
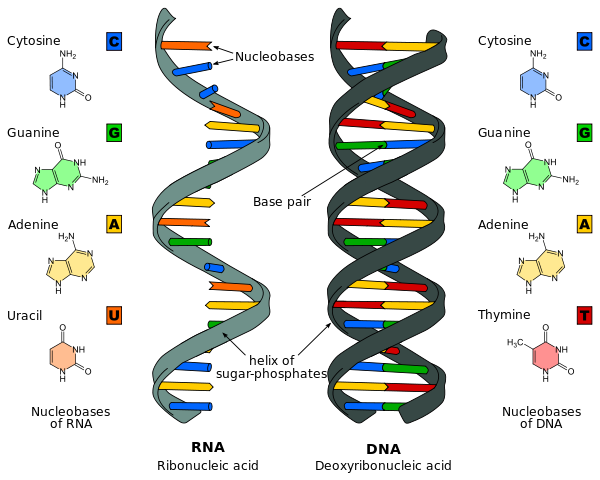
RNA and DNA. Image Roland 1952, CC B-SA 3.0.
Inheritance as a data transmission problem
Organisms inherit their genes from their parents. Asexual organisms, such as amoebae, inherit a complete copy of the genome of their parents. Sexual organisms (such as us) have two copies of each chromosome as they inherit one from each parent. The traits we inherit from our parents depend on how these combine.
Genes can acquire mutations in their sequence, leading to different variants of a trait, known as alleles, in the population. These alleles encode slightly different versions of a protein, which in turn cause different traits. It's through mutations that evolution occurs: if a random mutation proves beneficial for an organism, then that organism will pass the mutated gene on to its offspring. Mendel was the first to recognise that some alleles can be dominant and some recessive, which in part is a reason for the large variety that we see in inheritance.
The process of passing on information is done digitally. The RNA code that contains the template for producing proteins is designed to be read as triplets made of A, C, G and U. Each triplet is called a codon. Just about every living thing uses this exact code to make proteins from DNA. Codons are similar to the ASCII code used in computers to represent text. In the ASCII code individual letters are represented by a string of eight 0s and 1s.

RNA and DNA. Image Thomas Splettstoesser, CC B-SA 4.0.
Since a codon is a three-letter combination of the A C G U base pairs, there are 4x4x4=43=64 possible codons. These are used as codes for only twenty different amino acids, and also special "start" and "stop" codons that mark the beginning and end of a gene. This redundancy allows for the correction of errors. Suppose that in "reading" the codon for a particular amino acid an error is made and one of the three letters is misread. If the new triple is also associated to an amino acid, then we have a problem: the wrong amino acid is produced. If however, the codons for all the other amino acids differ in at least two letters from the scrambled-up triple, then it's easy to guess that an error has been made and to deduce which amino acid was really meant. (You can find out more about encoding information in a way that allows for fixing of mistakes in Error correction codes.) With 64 possibilities for codons for only twenty amino acids, there is plenty of room to choose the codons for the acids so that they are different enough for this error correction process to work.
Thus, the codons could be playing a similar role in the process of inheritance as the strings of 0s and 1s in error correction codes used by humans. We are not certain that nature really does use error correction codes in this way, but it certainly seems a very reasonable possibility given the discrete nature of the data and the obvious redundancy in the number of codons versus the number of amino acids. The use of this process of transmitting information is very effective and would only lead to errors in the order of one in 100 million. Does nature use other forms of error correction? At some level it must do, otherwise species could not reproduce reliably. However, fortunately (for us) this error correction does still allow for mutations to occur. Otherwise evolution would not be possible, and we would not be here.
In conclusion, we live in an information age, and the mathematical development of digital data transmission, combined with error correcting codes, allows us to communicate accurately and reliably. The processes used by nature to transmit information from one generation to another are also digital and highly reliable, and in many ways resemble digital communication methods. I hope that you will agree with me that maths is truly coded in our genes.
About this article
This article is based on a talk in Budd's ongoing Gresham College lecture series. A video of the talk is below.

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.
Comments
Chris G
I'm puzzled by the third para from the end about codon redundancy and how "it allows for the correction of errors", especially the sentence "If however the codons for all the other amino acids differ in at least two letters from the scrambled-up triple, the it's easy to guess that an error has been made and to deduce which amino acid was really meant".
Some concrete examples may help. Let's say the triplet GCU, which codes for alanine, is misread by one letter as GAU, which codes for aspartic acid. How do you get back from GAU to GCU? There are, and must be, other amino acids which differ only by one letter from GAU, for example GAA (glutamic acid), GGU (glycine). But even in those cases which differ by two from GAU, such as CGU (arginine), how is that relevant?
The most relevant passage from the companion article by Professor Budd, www.plus.maths.org/content/error-correcting-codes , seems to be the one about Hamming distances, but I just can't see how this applies here since there seems to be no question of adding extra parity digits.