How to compute the dimension of a fractal

We're all used to the idea of dimensions: a one-dimensional line, a two-dimensional square, a three-dimensional cube. You may have even heard of higher-dimensional shapes, such as the four-dimensional tesseract.

There are also shapes, called fractals, that can have fractional dimension. You might have heard of famous fractals such as the Mandelbrot set. But how can dimension be a fraction?

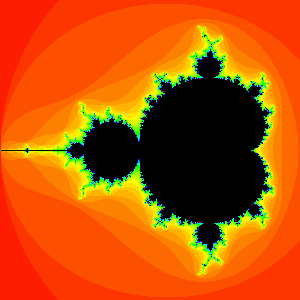
The Mandelbrot set

To find out, we have to first ask what we mean by dimension. And it’s not obvious! Depending on the context, different parts of mathematics will often use different definitions of dimension. Here we'll explore one definition of dimension well-suited for fractals, called Hausdorff dimension

Hausdorff dimension considers how the volume of a shape scales according to its size. We use volume here as a general term of measurement including length, area, volume, and so on. For example:

• Doubling the length of a line segment doubles its volume (ie, increases its volume by a factor of $2$).
• Doubling all the sides of a square increases its volume by a factor of $2^2$.
• Doubling all the sides of a cube increases its volume by a factor of $2^3$.

Hence we can think of dimension as follows: an object is $d$-dimensional if doubling its size in every direction increases its volume by a factor of $2^d$.

Now for the weird part.

A Sierpiński triangle is the fractal created by taking an equilateral triangle, dividing it into four smaller equilateral triangles, removing the centre triangle, and repeating the process on each of the three remaining triangles indefinitely.

Sierpiński's triangle.

Notice that a Sierpiński triangle is made up of three smaller Sierpiński triangles, each half the size of the original. That means that scaling a Sierpiński triangle by $2$ in all directions increases its area by a factor of… $3$?

Writing $3=2^{{\log }_{2}3}$, this means that Sierpiński triangles have dimension ${\log }_{2}3\approx 1.585$!

Let’s look at another fractal. The Koch Curve is the curve created by taking a line segment:

raising up its middle third to be an equilateral triangle tent:

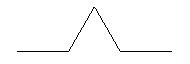
and repeating this on all the newly created line segments indefinitely.

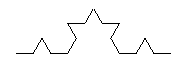
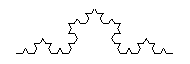
This time, the Koch curve is made up of four smaller copies of itself, each $1/3$ of its original size.

Previously we saw that if you doubled a $d$-dimensional shape (ie, you scaled all its sides by a factor of $2$) , then the volume of that shape increases by $2^d$. Similarly we expect that scaling a dimension $d$ shape by $3$ will increase its volume by $3^d$. In this case, scaling the Koch curve by $3$ gives four copies of itself, and so increases its volume by a factor of $4$! Writing $4=3^{{\log }_{3}4}$, we see that the Koch curve has dimension ${\log }_{3}4\approx 1.26$.

This way of computing dimension works well for fractals which are exactly self-similar, such as the Sierpiński triangle or the Koch curve. Computing the dimension of fractals in general is much harder. For example, it was only in 1998 that the Hausdorff dimension of the boundary of the Mandelbrot set was found to be exactly 2 by Mitsuhiro Shishikura.

Lastly, it is worth remembering that this notion of Hausdorff dimension is by no means obvious, nor is it the only way to define dimension. Sierpiński’s triangle and von Koch’s curve were originally created as examples in the process of teasing apart what would eventually become Hausdorff dimension from the older notion of topological dimension (any curve, no matter whether it is von Koch’s curve or space-filling, has topological dimension 1). For a long time these constructions were regarded mostly as mathematical curiosities; until in the 1970’s a mathematician named Benoit Mandelbrot realised that many shapes in nature, such as the coastline of Britain or the leaves of a fern, exhibit the same kinds of scaling properties that these earlier purely mathematical constructions had. He then went on to coin and popularise the term fractal to describe such shapes whose Hausdorff dimension exceeds their topological dimension, and fractals have been in the popular mathematical imagination ever since.

For more about fractals

• Read an overview about fractals here: Fantastic Fractals
• To see how computer-generated fractals can be used to model natural phenomena, look here: Modelling Nature with Fractals
• And look here for an explanation of music inspired by the self-similarity of fractals.