
How maths can make you rich and famous: Part II
A brief history of problem-solving
Despite the impression given by many textbooks, teachers and internet articles, we understand much less about mathematics than is commonly thought. In fact, maths is littered with problems that we cannot solve. Some are (possibly) not worth solving; some may not be solvable (in fact Gödel proved that there exist truly unsolvable problems); but there are some potentially solvable problems, the solutions of which would unlock the door to a lot of new mathematics and be of incalculable benefit to humankind. Indeed it is (probably) fair to say that much of mathematics, and indeed mathematicians, is stimulated by the desire to solve, and find, challenging problems.
Act one: the Greeks
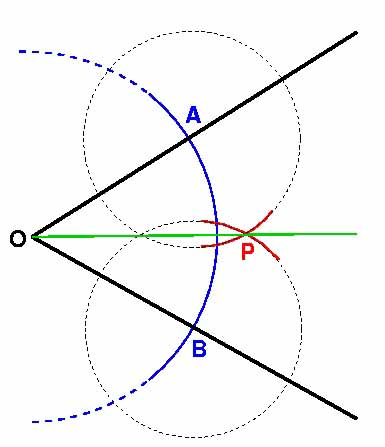
Bisecting an angle with a compass and straightedge
The Greeks were great mathematicians. An enormous amount of modern mathematics was discovered by Greek mathematicians such as Euclid, Pythagoras and Archimedes. The Greeks were best known for their discoveries in geometry, such as Pythagoras's theorem, the formula for the area of the circle and the Platonic solids. To do their geometry the Greeks used a ruler (to draw a straight line) and a compass. Using these simple tools they could construct equilateral triangles and hexagons and they could bisect any angle.
However, there were three problems that they could not solve using these methods. The first of these was trisecting an angle. It had been known since ancient times that any angle could be bisected, but the Greeks could find no way to trisect one. What they could not decide was whether there was a method for trisecting an angle, and they were too stupid to find it, or whether there was no possible method which could do the job. (There is more about angle trisection in Mathematical mysteries from Issue 7 of Plus.)
The second of the Greeks' problems was the question of the duplication of the cube. In a time of great famine a group of Greeks went to consult a sacred Oracle. The Oracle said that the famine would only stop if the Greeks could double the size of an altar. Doubling here meant finding an altar with precisely twice the volume of the original altar. Mathematically this means that the Greeks needed to construct a line of length equal to the cube-root of 2. The Greeks certainly knew how to construct the square-root of 2 (as the length of the hypotenuse of a right angle triangle) but had no idea how to find its cube-root. (It is unknown whether the failure of the Greeks to solve this problem meant that the famine continued.)
The final problem was that of squaring the circle, which involves constructing a line of length $\pi$ - for more on this, see Mathematical mysteries from Issue 21 of Plus.
All of these questions survived the Greeks unanswered, and indeed defeated the best efforts of the world's mathematicians for 2,000 years, but were finally solved in the 19th century. In each case it was shown that it was impossible for any method using just a ruler and compass to trisect an angle, double a cube or square the circle. (The proven impossibility of solving these problems does not prevent enthusiastic amateurs from not only trying to find ways to do the constructions but also sending their solutions to unfortunate professional mathematicians.)
Remarkably, the first two questions were resolved by Galois, a French mathematician who was only 21 when he died (in a duel). Galois' solution led to the invention of Galois theory, a beautiful area of mathematics which is now applied in constructing very reliable methods for communicating information.
Act two: Hilbert

David Hilbert
David Hilbert was probably the greatest mathematician of the end of the 19th and beginning of the 20th centuries. Among his many mathematical achievements can be included profound discoveries in logic, algebra and differential equations. Hilbert spaces, a special type of vector space, form the basis for the whole of quantum mechanics.
Hilbert was invited to speak at the International Congress of Mathematicians held in Paris in the year 1900. He could have given a (dull) talk on the achievements of mathematicians in the 19th century, but instead he did something far more interesting. At the start of the 20th century, Hilbert decided to throw out a challenge to keep mathematicians busy for the next 100 years. His talk comprised 23 problems, now called the Hilbert problems, the attempts to solve which he believed would stimulate 20th century mathematics and mathematicians. He chose his problems well. Not only have they proved immensely challenging to solve, but they have led to an enormous amount of new mathematics. Anyone who solved one of the Hilbert problems became extremely famous (within the mathematical community), but not necessarily very rich. Most of the Hilbert problems have now been solved. One which lasted until nearly the end of the 20th Century was Fermat's last theorem.
Pierre de Fermat was an French mathematician who worked in the 17th century and was interested in {\em number theory}. This is (essentially) the study of problems involving the natural numbers 1,2,3,\ldots. A test for prime numbers based on one of Fermat's results called {\em Fermat's little theorem} has just been discovered, and could play an important role in modern cryptography. It has been known since ancient times that you could find natural numbers $a$, $b$ and $c$ with $a^2 + b^2 = c^2$, an example being $3^2 + 4^2 = 5^2.$ In contrast, Fermat had managed to show that you {\em couldn't} find natural numbers with $a^4 + b^4 = c^4$, using a method he called {\em steepest descent}. He wondered whether, if $n$ was any integer different from 2, the problem $$a^n + b^n = c^n$$ had any whole-number solutions. While thinking about this he retreated to a library and read Diophantus's {\em Arithmetica}. It is not recorded whether he liked the text of the book, but he certainly did not like its margins - or to be more accurate the {\em size} of them. We know this because he wrote in the margin that he had found a {\em truly marvellous proof of the fact that the above problem could {\bf not} be solved, but unfortunately the margin of the book was too small to write it down}. Did he have a proof? To be honest, we don't know, and mathematicians have been trying hard ever since to find out (with extra points to be awarded to any proof that would fit into a book margin). The problem gained such notoriety that it was called {\em Fermat's last theorem}.

Andrew Wiles making history
Hilbert posed exactly this problem as one of his unknown problems at the start of the 20th century, and bang on cue, almost 100 years later, it was solved by Andrew Wiles as part of his proof of the Tatyana-Shumura conjecture. Fermat was right (but Wiles' solution will not fit into a margin). You can read about the story of this problem in the wonderful book Fermat's last theorem by Simon Singh.
Another of Hilbert's problems was the Riemann Hypothesis, which is not only still unsolved, but is generally regarded as the most important unsolved problem in mathematics. You can find out more about this problem in A whirlpool of numbers, also in this issue of Plus.
Act three: The Clay Institute
As we saw in How maths can make you rich and famous: Part I from the last issue of Plus, the Clay Institute has posed seven Millennium Prize Problems to perform the same function for 21st century mathematics as Hilbert's problems did for the 20th century. The sixth Millennium Prize Problem is the well-posedness of the Navier-Stokes equations.The Navier-Stokes equations

They didn't see this coming.
The aftermath of a hurricane in North Carolina.
Photo copyright FEMA
You may not have heard of the Navier-Stokes equations, but you encounter them every day. These are the equations that describe the weather!
We all know that the weather is important to our lives, that it can sometimes be predictable and other times very unpredictable. It seems strange that all of the different types of behaviour we associate with the weather can be described by a single set of equations, but we believe that this is the case. The subject of the sixth problem is a first, and vital, link in the chain of reasoning that we hope will establish exactly this fact.
We start by thinking about exactly what we mean by weather. Weather is the combination of the motion of the atmosphere, coupled to the motion of the oceans, the transport of moisture within the atmosphere, all coupled to changes in the pressure and temperature of the air. It is possible to write down (partial differential) equations which describe all of this mathematically. In their totality these equations are rather complicated, however at the guts of them are the equations that describe the underlying motion of the air on its own. These equations are the same for air as they are for water or any other fluid and they were derived in the 19th century by the two mathematicians Navier and Stokes, hence their name the Navier-Stokes equations.
Imagine that you are looking at a point $(x,y,z)$ in the atmosphere. At this point the air will have a {\em velocity} $(u,v,w)$ and a {\em pressure} $P$. These are all related together by the Navier-Stokes equations which describe how changes to the velocity in {\em time} are related to changes in the velocity and the pressure in {\em space}. Brace yourselves...here they come!
$$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x}+ v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} = -\frac{\partial P}{\partial x} + Re \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right),$$ $$\frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x}+ v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} = -\frac{\partial P}{\partial y} + Re \left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right),$$ $$\frac{\partial w}{\partial t} + u\frac{\partial w}{\partial x}+ v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} = -\frac{\partial P}{\partial z} + Re \left(\frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right),$$ $$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0.$$

Fluid mechanics with biscuits on the side.
Image DHD Photo Gallery
Although these equations look rather brutal, by the time you have done a university course in mathematics, physics or engineering they will become old friends. The term Re in the equations is called the Reynolds Number. It is low if the fluid is very sticky (like treacle) and high if it is hardly sticky at all, like air or water. What is really remarkable is that the same
equations describe the motion of the water in a cup of coffee, the evolution of a hurricane, the behaviour of the ocean currents and even the atmosphere of Jupiter - all of this physics is coded into one set of equations.

The red spot on the surface of Jupiter is a storm that has been raging for more than 300 years.
Composite image courtesy of NASA
Unfortunately there is some bad news to come. The first piece of bad news is that the Navier-Stokes equations are very, very hard to solve. We only know of a few exact solutions (that is, solutions which we can write down using a formula), usually for problems which are of little or no physical interest.
A lot of work has been done on finding approximate solutions which work for certain important physical situations, such as the flow of water in a pipe. The procedures for finding such solutions dominate the subject called fluid mechanics, which you may meet in a university course in applied mathematics, physics or engineering (especially aeronautical engineering). Fortunately it is possible to write computer programmes which can find numerical solutions to these equations. Indeed there is a huge industry called computational fluid dynamics devoted to this task. It is computer programs of this sort which are used by the meteorological office to help predict the weather. They are also used in the design of aircraft and cars, the study of blood flow, the design of power stations, the analysis of the effects of pollution, the study of the insides of a star, calculations of climate change and, in a notable success story, in the design of Thrust 2, the first supersonic racing car. (This calculation was done by the computational fluid dynamics team at the University of Swansea).

The Thrust SuperSonic Car breaking the sound barrier in Blackrock Desert,
Nevada on 15th October 1997. Picture copyright Andy Graves
The next piece of bad news is that even in the best of circumstances these programs can take even the fastest computer an enormous time to run, and these computers can often only solve relatively simple problems. They are also quite unable to deal with the phenomenon called turbulence. Turbulence is the complex behaviour that fluids show on small length scales. (An understanding of turbulence is one of the great problems in physics for the new millennium.) You can see or feel turbulence every time that you look at a cloud, examine the motion of the water in a waterfall or stick your head out of a car window. No computer programme on earth can simulate this behaviour exactly, and at the present all that we have are rough approximations. It is a sobering thought that these approximations have to be used every time a simulation is made of a safety-critical situation (such as the effects of a fire or of a coolant leak in a nuclear power station). The approximations are not bad (giving errors of around 20%), but this situation is hardly satisfactory.
All of the above issues are very important to the way that we use the Navier-Stokes equations to help us to understand the physical world around us, but they pale into insignificance when compared to the subject of the sixth Millennium Prize Problem. This is not whether we can solve the Navier-Stokes equations (either exactly or using a computer), but whether they have any solutions at all.
You may feel that this is an unimportant question - after all it is obvious - isn't it? - that the equations must have a solution. However there are plenty of examples in mathematics of equations which don't have solutions. For example, before the invention of negative numbers, the equation x+1=0 had no solution. The Greeks thought that all numbers could be expressed in terms of fractions (rational numbers) and had a very deep shock when they discovered that the equation x2=2 did not have a solution which could be expressed as a fraction. Similarly, if you only knew about real numbers then it would not be possible to solve the equation x2=-1. It is quite possible that a situation could occur in which a possible solution of the Navier-Stokes equations starts by being completely physical, but quickly becomes infinite and fails to represent anything corresponding to the physical situation that the equations are trying to describe.
The present situation is that noone has managed to show that the solutions of the Navier-Stokes equations correspond to real physical solutions for all time. Conversely, noone has found a "solution" of the Navier-Stokes equations that becomes infinite and loses its physical meaning. If such a solution were to be found, would it really be nonsense or might it give us some insight into the problem of turbulence (the latter being the view of the author)? We don't know! What we do know is that for the cases that we can compute, the Navier-Stokes equations do seem to give a very accurate description of the motion of fluids and that they also seem to be uniquely hard. Make a small change to the equations and we can answer all of the questions, but return to the physically motivated equations and nothing is certain. Mathematicians seem evenly divided as to whether solutions exist or not and the question of the existence of solutions seems likely to stay unresolved for a long time.
Conclusion
As I said in Part I in the previous issue of Plus, solving one of the Millennium Prize Problems would give you a form of mathematical immortality and maybe even fame and fortune. My advice to any of you who think that you might have a crack at one of the problems is go for it! Remember that the problems the Greeks left us were not only answered, but were answered by a 21 year old mathematician.And remember that maths can make you rich and famous in many other ways as it unlocks the doors to a huge number of interesting and varied careers.
About the author

Chris Budd is Professor of Applied Mathematics at the University of Bath, and Chair of Mathematics for the Royal Institution. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has recently co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin.
This article now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
Anonymous
I liked how you argued how there are and were plenty of examples of equations which don't have exact solutions.
My question is, is there room for a "new" number system, perhaps the super-complex numbers, that solve these equations? After all, this is how we have solved "illegal" equations throughout history.
Great article, many thanks!
Anonymous
But according to Fundamental Theorem of Algebra, we can find all solutions to an equations by complex numbers.