
Infinity or -1/12?
Recently a very strange result has been making the rounds. It says that when you add up all the natural numbers
1+2+3+4+...
then the answer to this sum is -1/12. The idea featured in a Numberphile video (see below), which claims to prove the result and also says that it's used all over the place in physics. People found the idea so astounding that it even made it into the New York Times. So what does this all mean?
The maths
First of all, the infinite sum of all the natural number is not equal to -1/12. You can easily convince yourself of this by tapping into your calculator the partial sums
$$S_1 = 1$$ $$S_2 = 1+2 = 3$$ $$S_3 = 1+2+3=6$$ $$S_4 = 1+2+3+4=10$$ $$...$$ $$S_n = 1+2+3+4+ ... +n,$$ and so on. The $S_n$ get larger and larger the larger $n$ gets, that is, the more natural numbers you include. In fact, you can make $S_n$ as large as you like by choosing $n$ large enough. For example, for $n=1000$ you get $$S_n = 500,500,$$ and for $n = 100,000$ you get $$S_n = 5,000,050,000.$$ This is why mathematicians say that the sum $$1+2+3+4+ ... $$ diverges to infinity. Or, to put it more loosely, that the sum is equal to infinity.

Srinivasa Ramanujan
So where does the -1/12 come from? The wrong result actually appeared in the work of the famous Indian mathematician Srinivasa Ramanujan in 1913 (see this article for more information). But Ramanujan knew what he was doing and had a reason for writing it down. He had been working on what is called the Euler zeta function. To understand what that is, first consider the infinite sum
$$S = 1+1/4+1/9+1/16+ ... .$$ You might recognise this as the sum you get when you take each natural number, square it, and then take the reciprocal: $$S = 1+1/2^2+1/3^2+1/4^2... .$$ Now this sum does not diverge. If you take the sequence of partial sums as we did above,
$$S_1 = 1$$ $$S_2 = 1+1/2^2 = 5/4=1.25$$ $$S_3 = 1+1/2^2+1/3^2 = 49/36 = 1.361...$$ $$...$$ $$S_n =1+1/2^2+1/3^2 + ... + 1/n^2,$$
then the results you get get arbitrarily close, without ever exceeding, the number $\pi^2/6 = 1.644934... .$ Mathematicians say the sum converges to $\pi^2/6$, or more loosely, that it equals $\pi^2/6.$ Now what happens when instead of raising those natural numbers in the denominator to the power of 2, you raise it to some other power $x$? It turns out that the corresponding sum $$S(x) = 1+1/2^x+1/3^x+1/4^x... $$ converges to a finite value as long as the power $x$ is a number greater than $1$. For every $x > 1$, the expression $S(x)$ has a well-defined, finite value. $S(x)$ is what's called a function, and it's called the Euler zeta function after the prolific 18th century mathematician Leonhard Euler. So far, so good. But what happens when you plug in a value of $x$ that is less than 1? For example, what if you plug in $x=-1$? Let's see. $$ S(-1) = 1+1/2^{-1}+1/3^{-1}+1/4^{-1}... $$ $$ = 1+2+3+4+ ... .$$ So you recover our original sum, which, as we know, diverges. The same is true for any other values of $x$ less than or equal to 1: the sum diverges.
Extending the Euler zeta function
As it stands the Euler zeta function S(x) is defined for real numbers x that are greater than 1. The real numbers are part of a larger family of numbers called the complex numbers. And while the real numbers correspond to all the points along an infinitely long line, the complex numbers correspond to all the points on a plane, containing the real number line. That plane is called the complex plane. Just as you can define functions that take real numbers as input you can define functions that take complex numbers as input.
One amazing thing about functions of complex numbers is that if you know the function sufficiently well for some set of inputs, then (up to some technical details) you can know the value of the function everywhere else on the complex plane. This method of extending the definition of a function is known as analytic continuation. The Euler zeta function is defined for real numbers greater than 1. Since real numbers are also complex numbers, we can regard it as a complex function and then apply analytic continuation to get a new function, defined on the whole plane but agreeing with the Euler zeta function for real numbers greater than 1. That's the Riemann zeta function.
But there is also another thing you can do. Using some high-powered mathematics (known as complex analysis, see the box) there is a way of extending the definition of the Euler zeta function to numbers $x$ less than or equal to 1 in a way that gives you finite values. In other words, there is a way of defining a new function, call it $\zeta(x),$ so that for $x>1$ $$\zeta(x) = S(x) = 1+1/2^x+1/3^x+1/4^x...,$$ and for $x\leq 1$ the function $\zeta(x)$ has well-defined, finite values. This method of extension is called analytic continuation and the new function you get is called the Riemann zeta function, after the 19th cenury mathematician Bernhard Riemann. (Making this new function give you finite values for $x \leq -1$ involves cleverly subtracting another divergent sum, so that the infinity from the first divergent sum minus the infinity from the second divergent sum gives you something finite.) OK. So now we have a function $\zeta(s)$ that agrees with Euler's zeta function $S(x)$ when you plug in values $x>1$. When you plug in values $x \leq 1$, the zeta function gives you a finite output. What value do you get when you plug $x=-1$ into the zeta function? You've guessed it: $$\zeta(-1)=-1/12.$$ If you now make the mistake of believing that $\zeta(x) = S(x)$ for $x=-1$, then you get the (wrong) expression $$S(-1) = 1+2+3+4+ ... = \zeta(-1) = -1/12.$$ This is one way of making sense of Ramanujan's mysterious expression.
The trick
So how did the people in the Numberphile video "prove" that the natural numbers all add up to -1/12? The real answer is that they didn't. Watching the video is like watching a magician and trying to spot them slipping the rabbit into the hat. Step one of the "proof" tries to persuade you of something rather silly, namely that the infinite sum $$1-1+1-1+1-....$$ is equal to $1/2.$ The video doesn't dwell long on this and seems to imply it's obvious. But let's look at it a little closer to see if it makes sense at all. Suppose that the sum $1-1+1-1+1-1....$ has a finite value and call it $Z$. Adding $Z$ to itself you get the infinite sum $$Z+Z = 1-1+1-1+1-....+1-1+1-1+1-... .$$ But this is just the original sum, implying $$Z+Z=2Z = Z.$$ Since $Z=1/2,$ it follows that $1/2=1,$ which is nonsense. So the assertion that the infinite sum $1-1+1-1+1-....$ can be taken to equal to 1/2 is not correct. In fact, you can derive all sorts of results messing around with infinite sums that diverge (see here). It's a trick!
The physics
But how did this curious, wrong result make it into a physics textbook, as shown in the video? Here is where things really get interesting. Suppose you take two conducting metallic plates and arrange them in a vacuum so that they are parallel to each other. According to classical physics, there shouldn't be any net force acting between the two plates.
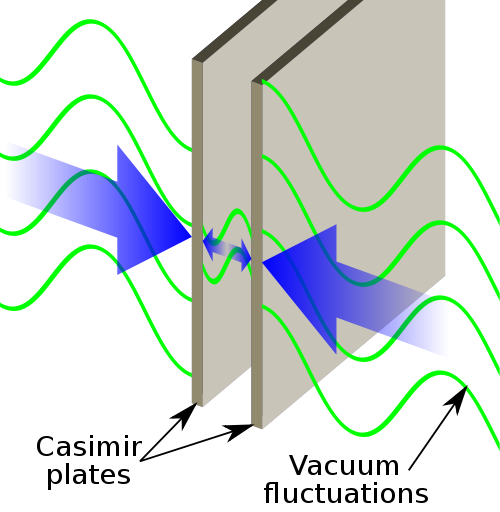
Illustration of the Casimir effect. Image: Emok.
But classical physics doesn't reckon with the weird effects you see when you look at the world at very small scales. To do that, you need quantum physics, which tells us many very strange things. One of them is that the vacuum isn't empty, but seething with activity. So-called virtual particles pop in and out of existence all the time. This activity gives a so called zero point energy: the lowest energy something can have is never zero (see here for more detail).
When you try to calculate the total energy density between the two plates using the mathematics of quantum physics, you get the infinite sum
$$1 + 8 + 27 + 64 +... .$$ This infinite sum is also what you get when you plug the value $x=-3$ into the Euler zeta function: $$S(-3) = 1 + 1/2^{-3} + 1/3^{-3} + 1/4^{-3} + ... = 1+ 8 + 27 + 64 +... .$$ That's unfortunate, because the sum diverges (it does so even quicker than than $S(-1)$), which would imply an infinite energy density. That's obviously nonsense. But what if you cheekily assume that the infinite sum equals the Riemann zeta function, rather than the Euler zeta function, evaluated at $x=-3$? Well, then you get a finite energy density. That means there should be an attractive force between the metallic plates, which also seems ludicrous, since classical physics suggests there should be no force. But here's the surprise. When physicists made the experiment they found that the force did exist — and it corresponded to an energy density exactly equal to $\zeta(-3)$!
This surprising physical result is known as the Casimir effect, after the Dutch physicist Hendrik Casimir.
Take a moment to take this in. Quantum physics says the energy density should be $$S(-3) = 1+8+27+64+... .$$ That's nonsense, but experiments show that if you (wrongly) regard this sum as the zeta function $\zeta(x)$ evaluated at $x=-3$, you get the correct answer. So it seems that nature has followed the ideas we explained above. It extended the Euler zeta function to include values for $x$ that are less than 1, by cleverly subtracting infinity, and so came up with a finite value. That's remarkable! The reason why we see $\zeta(-1)$ and $S(-1)$ in the Numberphile video and the physics textbook, rather than $\zeta(-3)$ and $S(-3),$ is that when you imagine the Casimir effect as happening in one dimension (along a line rather than in 3D), the energy density you calculate is $\zeta(-1)$ rather than $\zeta(-3)$.
So why did the Numberphile people publicise this strange "result"? They certainly know about the analytic continuation that makes the function well-defined, but that was something that was a little too technical for their video. Knowing they had the analytic continuation method, that would make the final result OK, hidden in their back pocket, they went ahead with their sleight of hand. In doing so they got over a million hits and had the world talking about zeta functions and mathematics. For this they should be congratulated. The mathematics of zeta functions is fantastic and what we described here is just the start of a long list of amazing mathematical properties. In bringing mathematics and physics to the public we always have to make choices about what we leave out and what we explain. Where to draw that line is something we all have to leave to our consciences.
About the authors

David Berman is a Reader in Theoretical Physics at Queen Mary, University of London. He previously spent time at the universities of Manchester, Brussels, Durham, Utrecht, Groningen, Jerusalem and Cambridge as well as a year at CERN in Geneva. His interests outside of physics include football, music and theatre and the arts.
Marianne Freiberger is editor of Plus.
Comments
Anonymous
Dear David and Marianne,
Thank you for the interesting explanations. I would remark, though, that the summation "1-1+1-1+... = 1/2" is not the source of fallacy in the Numberphile video. That series, while not convergent, is still "Cesaro summable" [which means, that the average value of its first n partial sums converges in the limit as n is taken to infinity].
The Cesaro sum of series has many nice properties, e.g., allowing a certain class of rearrangements of the terms, allowing the sums to be added when Cesaro summable series are added term by term, etc. The fallacies enter elsewhere, in the various manipulations of divergent and non-Cesaro summable series. Such manipulations can be used to arrive at any value at all for the sum of all the natural numbers.
Perhaps others have already made this point, as I've not viewed all of the linked and related sites.
Like others, I too would have wished to see some indication in the Numberphile video of the "tongue in cheek" nature of the "proof," without losing the huge entertainment value. Fallacies (like "proving" that 1 = 0 with a hidden divisioon by zero in the algebra) have always been a source of fun and exploration in school mathematics.
Here, the video is understandable to many middle grades students as well as high school students; this is great! But their teachers then need to know it is "sleight of hand," and encourage their students to question the "authority" behind it. Teaching mathematics by authority rather than through understanding is a continuing, unfortunate trend in our schools, at least in the USA, and I cannot help but feel an opportunity here might be being missed.
Gerald Goldin
Rutgers University
Anonymous
Disclaimer: I'm just a 7th grader who's smart, so don't trust me on this.
Alright, so there actually is a different proof that 1-1+1-1+1...=1/2. First, let's consider this way of solving this convergent series, namely 1+1/2+1/4+1/8.... We already know this sums to 2.
Let us call this series S. Then 2S=2+1+1/2+1/4+1/8... = 2+S.
2S=2+S
S=2
We can use similar methods to work with divergent series and other series. If 1-1+1-1+1-1... equals S, then S+S=1-1+1-1+1...+1-1+1-1+1-1...
Shift the second S over by one term, and all terms after the first in the first S get canceled out, leaving us with 2S=1 and S=0.5.
Similar methods are used in the final proof.
Anonymous
There is no single unique "value" obtainable for a nonconvergent series through rearranging, regrouping, adding, etc. nonconvergent series. If you check out comments for the Numberphile video, you can find several different values produced for the same series, and although many of them are done incorrectly there are still several cases that correctly perform operations that would be allowed for convergent series. Once you have several different values all "equal" to the same thing, you can in principle derive all sorts of nonsense including 1=0.
Anonymous
You're not justified in shifting the terms over. You can't arbitrarily add 0-values to an infinite sum. And if you think about it conceptually you cannot move a line that extends to infinity, you would be stretching/compressing it.
Also to compare the functions S and S' vertically by adding 0 at the beginning of S', then you would need to add 0 at the end of S. This is obviously not possible.
Connor Smith
Adding a zero doesn't change anything about a series. And he is justified in his calculations.
Anonymous
Thanks for your comments, I agree completely
David
Anonymous
In order to find the sum of this series, first of all, the sequence of the partial sums must converge. However, the sequence of partial sums does not converge. Rather, it oscillates between 0 and 1.
Thus, insofar as the sequence does not converge there is no reason to talk about a unique sum of the series. In this case we can prove anything we want: 1, 1/2...
Anonymous
I saw a demonstration of this sum recently. It went like this:
S=1-1+1-1+...
=1-(1-1+1-...)
the periods indicating a continuation to infinity, it is assumed that:
S=1-S
2S=1
S=1/2
Then again, the alternating harmonic series converges to ln2 but by rearranging the terms in the equation, it also converges to (ln2)/2 and (ln2)/4 and so forth. The problem in your reasoning is that you take a partial sum as reference. I know that it's counter-intuitive just like 0.00000...1= 0 but the reason it gives that result is only because the sum is infinite. The moment it becomes finite, these results all go wrong.
Anonymous
So isn't this series basically sigma of n for which n starts from 1 and ends at infinity? In this case, in my opinion, as every terms in this series is positive, this series can immediately be included in the 'comparison tests for convergence and divergence'. French mathematician Nicole Oresme has proved the divergence of the harmonic series 1/n by proving the divergence of a series which has lesser terms than that of the harmonic series. If, as what the numberphile people are saying, 1+2+3+4+... forever does equals to -1/12 doesn't this make the whole concept of comparison test flawed? Even if the Grandi's series which is 1-1+1-1+1-1... does actually equals to a half, the answer 1+2+3+4+.. forever does not make sense as it makes previous proofs and statements made in infinite series incorrect.
Also, i don't understand what the average partial sums are for. Why is there the need to average the partial sums? The average of the partial sums may converge towards a half but that doesn't mean anything that the 'non-average' (as in real) series converge towards a half...
Anonymous
One of the guys in the vid says there's a proof for Z (the Grandi series) = 1/2. I'll leave that to the more advanced, but to me that makes sense intuitively. In the absence of a graph for now, imagine a horizontal wavy line ascending with every +1 to a peak at 1 on the y axis and descending with -1 again to 0. Repeat, say with six 1's, so for three cycles. Now draw another horizontal straight line skimming along from peak to peak, and clearly you will have a figure falling into two equal halves above and below the wavy line. Each of these two halves will also equal the halves created by yet another horizontal straight line drawn from .5 on the y axis.
Now for the smart bit. Do an Oresme on the series, rearrange the +1's and the -1's into different, though still zero sum cycles: +1+1+1-1-1-1. This time the amplitude will rise to 3 and the horizontal through the mid points will be at 1.5, so the sum of the series will be 3/2.
This hocus pocus, if you want to call it that, also has an echo in nature. I've just been learning about Cepheid variable stars, and the close direct relationship between luminosity and the period over which luminosity varies from minimum to maximum and back. Luminosity, energy emitted per unit of time, could be represented by the area under the wavy line maybe. How the values 1/2 and 3/2 would relate to the natural parameters of luminosity and period I don't know, but any comments gratefully received.
Anonymous
Averaging the partial sums is the simplest case of what's known as Cesàro sums. Here's why that technique is attractive: If the original series converges to a particular value, so does its Cesàro sum; if the original series diverges, so does its Cesàro sum. For series that are neither convergent nor divergent, such as the Grandi series, sometimes the Cesàro sum produces a definite finite value. Some people (not I!) therefore think that the Cesàro sum can be used in place of the standard sum.
Anonymous
The guys in the video mention that they know the answer must be -1/12 because that result allows them to make other accurate calculations regarding string theory. Well, are there any exmaples that show it the answer can or cannot be -1/12?
Anonymous
With my little knowledge on maths I think you made a mistake.I was actually bugged about infinity sums for a while but I slowly start to understand them thankst your maths.You said Z+Z=1-1+1-1...1-1+1-1 which equals to Z.Well there's a problem in your maths!You seem to think that Z is actually ending and another Z begins!The Z function never ends and that's why you can't add something on the end of an infinite function!That's why I think (with my basic math knowledge) you shouldn't add a Z function to the end of another Z function!Because you don't know if the Z function will end with a 1 or a -1!The best approach of how much Z+Z is this:
Z+Z=1+1-1-1+1+1-1-1...=2(1-1+1-1+....)=2*1/2=1
Thank for a great night read :)
Anonymous
Z = 1 - 1 + 1 - 1 + 1.....
Z' =0 +1 - 1 +1 - 1.....
Z+Z' => All but the 1st term cancel out, leaving just 1.
2Z = 1.
Z = 0.5
Or another way:
Z = 1 - 1 + 1 - 1 + 1.....
Z = 1 - 1 + 1 - 1 + 1.....
2Z = 2 - 2 + 2 - 2 + 2.....
So, 2Z is either 2 or 0; average 1.
2Z = 1.
Z = 0.5
Anonymous
1-1+1-1+1-1...+1-1+1-1+1... = 2Z.
It does not equal Z as the article states.
Anonymous
You keep saying this sum is 'wrong.' Of course, it's not. Obviously, if you EVER stop at any point while taking this sum, you'll end up at a positive, finite, and possibly massive number. But the point is, your are taking the sum to infinity, meaning that there ISN'T a stopping point. The sum of all positive integers is -1/12, and it's been proven (the zeta function is real and completely valid); it's not 'wrong' just because it doesn't make sense.
Also, (interesting but perhaps unrelated) if you take the ideas used to calculate this sum, you can find that the sum of all odd positive integers is +1/12 the sum of all positive even integers is -1/6.
Anonymous
Can someone comment on this? I no longer believe anything!!!
Anonymous
Listen carefully in the explanation video. At one point, the man suggests the series s1 = 1 - 1 + 1 - 1 ... should be taken to be 1/2. The reasoning he gives for this is that "if we stop at an odd point the sum equals 1, if we stop at an even point then the sum equals 0". Both of those are true on their own, but hold on. If we "stop" at a point to observe a value, then that value must just based on that one part of the total sum. We can derive a value by averaging two repeating parts of our sum, but this means that the value is based on the parts, not the sum itself. the fact that the series 1 - 1 + 1 - 1 ... is cyclic (repeats the same pattern of numbers) allowed the presenter to derive a fact about all the parts at once, but this fact was not the sum of the series. The rest of their calculations are all derived from this one, and thus are all based upon facts about the parts that make up the sum, rather than what it equals, or "sums". This doesn't mean that the calculations are useless, though. These numbers represent facts about the sums that could prove useful.
Anonymous
Thank you very much for this eloquent and succinct article. It's restored my faith in "intuition".
We are in an era where the rush to publish a "result" for reward or attention has never been greater. It seems rigour is taking a back seat in this new era, so we must stay on our toes if we are to find truth amidst all the noise.
Anonymous
I like the explanation here distinguishing between the Reimann and Euler zeta functions, but I am still skeptical about their use in characterizing divergent sums.
Even though the Reimann zeta function gives a value for the attraction between two metal plates in a vacuum that matches the value given my QM, it still does not make the sum of the natural numbers or QM any more real. Sure, the both have utility in explaining things: i.e. the force between two plates, but that does not definitively exclude other possibilities.
Galileo sort of argued this for planetary motion to appease the church: you don't have to really believe that the Earth revolves around the sun, but if you want predict where planets will be, you can do the math as if the Earth does revolve around the sun.
And Einstein's general relativity: An elevator sitting in a gravitational field behaves as if we are in an elevator in an accelerating spaceship. Since there is no distinguishing these two scenarios, they are equivalent.
Finally, if Fourier series can represent other functions (I am thinking about X-ray crystallography) then which is more real: the Fourier co-efficients or the values of the real function. If they can both represent the same thing, but it is useful to use one sometimes and the other at other times, can one be more real than the other?
Back to QM and the sum or natural numbers... I wonder whether the treatment of the problem is incorrect (unreal) in both cases, but it cancels each other out to arrive at accurate values. Aren't there other theories still around that describe subatomic events without invoking QM? If these are applied to the Casimir plates, maybe it bypasses the Euler zeta function and uses the Reimann zeta function.
Anonymous
OMG !! What Have YOU Done?????
Z+Z= the original sum i.e. Z
so you write 2Z=Z
so putting Z=0.5, we get 0.5=1
but why stop here?
It's an infinite sum so at my will I can write (Z+Z = Z+Z) or (Z+Z = Z+Z+Z+.........+Z)
so, Z=Z or Z=nZ
so whatever Z is, Z can be anything else....it's nonsense. RIGHT??
Don't stop. It's not like counting bricks. Whenever you put an end to it, its a divergent series and for that don't assign any value for GOD's sake!
BUT, try to think it this way. The sum is indeed INFINITE. That is the only truth. It doesn't end. But that infinite is a pile of junk. There is a bit of finite part in that infinity. Whenever you stop and calculate, each time it blows up. But there is this (-1/12) part which only accumulates if you allow it to go on forever. And yes we physicists use it in quantum fields and all sort of places. Each time we replace that infinite sum with this very value, we confirm the result! Don't teach things you don't fully understand.
Anonymous
//OMG !! What Have YOU Done?????
Z+Z= the original sum i.e. Z
so you write 2Z=Z
so putting Z=0.5, we get 0.5=1
but why stop here?
It's an infinite sum so at my will I can write (Z+Z = Z+Z) or (Z+Z = Z+Z+Z+.........+Z)
so, Z=Z or Z=nZ
so whatever Z is, Z can be anything else....it's nonsense. RIGHT??//
genius this is the exact point they also made :p really ROFL
Anonymous
This is the problem w infinite sums and calculus...people don't know all the rules, and make folly out of the work done by geniuses before them.
You cannot add infinites like numbers, because they're not numbers! We've found cheeky ways of representing infinity w finite numbers, but infinity , itself, is beyond what our finite minds can truly imagine.
Either way, when you Transpose the infinite concept into our finite world, finite operations work with the finite representation.
Assume infinite sum of numbers (1+2+3+4...) IS equal to -1/12 (we can assume this because we proved it is. Like we proved 2+2=4, or other convergent infinite sums). Let this equal Z
Using the new finite concept, Z+Z is -1/6, which is the same as 2Z..true!
Z+Z =/= Z+Z+Z...Z because you're mixing together the finite and infinite worlds.
2Z=/= nZ except when n=2. This is true using our finite point of view. Not with the infinite point of view. Remember, we only use Z to represent the finite value. If we don't take this value into consideration (we don't use proper infinity aka, we use a REALLY LARGE NUMBER), it breaks apart. Because we aren't using Z anymore.
Also, assuming S=1-1+1-1+1-1+... it's the same deal. Once you STOP, or if you don't use infinity properly, you will get a finite value, which is not infinite, and therefore not S. In the case of Z, if you stop early, you get a huge number, not -1/12. Same here, if you stop randomly, you get S=0 or 1, not 1/2. In infinite space, unfathomable to us, (finite things are unfathomable to us) it would converge (practically, since we're transposing it to our finite world, as with any convergent infinite sum).
Anonymous
Z+Z=Z. This works if only the first infinite series ends with a -1. But its infinite... doesn't end. so the argument is invalid
Anonymous
My apologies about this, my comment is not about the sums but about the casimir effect. You mentioned that classical physics says that there should be no net force between the plates. But my high-school science teacher told us that there is a gravitational force acting between any two masses.
Anonymous
There would be a gravitational force as well, but the unexpected result is an electromagnetic force. The plates are electrically neutral so you wouldn't expect any attraction, but the zero-point energy of the vacuum indeed draws them together/apart.
Anonymous
That's because the article is wrong, and little backdoors like this are tricking you into thinking the sum is infinity.
-1/12 is the correct answer.
I'm Einstein's ghost.
Anonymous
Thank you. One person who got it correct.
Anonymous
" Knowing they had the analytic continuation method, that would make the final result OK, hidden in their back pocket, they went ahead with their sleight of hand. In doing so they got over a million hits and had the world talking about zeta functions and mathematics. For this they should be congratulated. "
I think spreading ignorance will rather attract ignorant fan-boys and repel those with rational reasoning.
Anonymous
I disagree, because I've seen this video and got curious, I've found this article and now I understand.
Anonymous
I think they could have been a bit clearer that this is a sleight of hand though.
Anonymous
If Z(-1) = 1+2+3+4+5+....= -1/12. & Z(0) = 1/1^0 +1/2^0 +1/3^0 +1/4^0 +...
Z(0) = 1+1+1+1+1+...
[Z(-1) +Z(0)] = 2+3+4+5+... = 1+2+3+4+5+... -1= -1/12 -1 = -13/12
This implies Z(0) = -1
[Z(-1) - Z(0)] = 0 + (1+2+3+4+5...) = -1/12
This implies Z(0) = 0
Both these values for Z(0) of -1 & 0 are contradictory.
Adding [Z(-1) + Z(0)] + [Z(-1) - Z(0)] = -13/12 -1/2 = -14/12 = -7/6
This implies 2Z(-1) = -7/6 => Z(-1) = -7/12This contradicts Z(-1) = -1/12 which
was the original assumption.
Putting infinite divergent series equal to a finite number appears to lead to
results that are not sensible.
Anonymous
Consider these two divergent series.
Sp = +1 + 1 + 1 ....
Sn = -1 - 1 - 1 ...
If added together, all terms cancel and Sp + Sn = 0.
However, if one allows the illegitimate preliminary step of "shifting" either series left or right, one can arbitrarily produce a result of any integer value you want to get. The operation of shifting (or of defining a "series" that starts with a finite number of zeros) creates a finite series that becomes the result. The amount of shifting determines the number you get, because the rest of the infinite series will still cancel.
BTW, notice also that Sp + Sn = S1 from the video. So, if one rules out illegitimate cheating steps that artificially create a finite series (e.g. shifting or bracketing), the result is that Sp + Sn = S1 = 0.
Anonymous
Some of positive natural numbers is n(n+1)/2
So if we put n(n+1)/2 =-1/12 we get value of n less than 1.
So....what?
Anonymous
Let's take our sum to infinity where the sum is supposed to be -1/12. Then let's add -1/12 to each side, and the sum is now zero. Am I missing something? Actually the whole edifice of this folly seems to be that these people treat infinity as if it were a number. Now if I can add 1/12 to infinity, it really wasn't infinity anyway. The series cannot converge unless there is a fudge factor, and that fudge factor is a game on paper, (and in some peoples' heads), that doesn't exist in nature (and logic). After all, nature doesn't work with infinitesimals: The shortest time is Planck time is 10**-43 seconds, and the shortest distance is 10**-35 metres. These are not because our tools are not good enough to measure them, it's because these are the smallest packets of time and distance that occur in nature. So the modern day versions of Zeno's paradoxes fail because they arbitrarily assign values to infinity and infinitesimals when required, and remove them when it doesn't suit the purpose. Infinity is still a theoretical, and non-real concept. If nature doesn't use it, then neither should we.
Anonymous
I must disagree with your assumption that we should not use anything not seen in nature in Mathematics. That may be a useful viewpoint in some sciences, but Mathematics often disconnects itself with reality only for the reality that belongs with it to be found later. In the 1500s, complex numbers were regarded as a ridiculous concept, yet now they are well accepted, their properties well documented, and natural cases have been found where they are used frequently. In electrical engineering, for example, heavy use is made of complex numbers. The concepts of infinitesimal and infinity are indeed quite necessary, as without it the idea of convergence and differentiation are less well-defined, perhaps impossible. So if your job, whether by its nature, its equipment, or otherwise relies on calculus, you do indeed need infinitesimals. Avogadro's number and the speed of light as values are solely decided by the measurements we use to find them, while π, e, γ, ρ, and many other Mathematical constant's don't change, regardless of measurement.
Anonymous Squared
Your understanding of Planck units is flawed. Planck unit are merely a system of natural units in which G, c, and h-bar have a value of 1. Nothing in physics prevents values smaller than Planck units. For instance, calculate the Planck energy unit. It is huge compared to the energy of the battery in my cell phone, or the energy of a photon of visible light.
Anonymous
Extreme care is needed when dealing with infinite sums. From what I can tell, it seems that confusion arises when people assume they are allowed to manipulate infinite sums in the same way as they are used to doing with the finite sums they are accustomed to dealing with. Assuming infinite sums behave anything like finite sums will lead to problems. Reordering a non-convergent infinite sum will often produce different answers - in many cases you can get any result you desire, but it's clearly incorrect. Proceeding term-by-term to calculate the partial sums. What does it even mean to sum an infinite number of terms when the sum is non-convergent? It's unsafe to assume that what works for finite sums must apply to infinite sums as well.
Regarding -1 + -1 ... (Grandi's Series), although it doesn't have a limit, it is Cesaro summable and as a cesaro sum of 1/2. This can be easily proved in lots of ways. This is what Numberphile were talking about no doubt.
Anonymous
I was pretty blow away at that stage of the "proof." Let's just say the infinite series 1-1+1-1+1-1+1-1... is solved by averaging 0 and 1? what? There may be an explanation but that is not it.
Anonymous
They said that for the sake of time. If you re-watch the video you'll see a link to a previous video dealing with that series in greater detail.
Anonymous
This website hammers down on the first sum Numberphile uses, 1-1+1-1+...
This is called Grandi's series, look it up anywhere and you will find the answer IS 1/2, because of simple algebra.
People are always like "You can't use algebra on infinities", I have to respectfully disagree. In order to figure out infinities, you treat them like variables. The only difference between infinity and x is infinity can't equal something, x can. So when dealing with sums, we can treat infinity like a variable and figure out the sum from there. This is pretty much what Numberphile did the entire video excluding Grandi's series, which can be proven multiple ways elsewhere on the internet.
Anonymous
In the sum, substitute 1+1 for 2, 1+1+1 for 3, etc to get 1+1+1..., now do it with the even numbers, then the odd, then the primes, all result in 1+1+1 forever. Do they all equal -1/12?
Anonymous
What about following sum?
-infinity.........+-3 + -2 + -1 + 0 + 1 + 2 + 3 .........+infinity
I guess answer to this is -1/12 :)
1+2+3+4+5+....+infinity = infinity
You can only play around by switching positions in a series if you consider both ends because its infinite series..
Anonymous
Another you-tuber mathologer proved this in his video but I somehow still don't get it. Here's the link: https://www.youtube.com/watch?v=jcKRGpMiVTw
m_muller
So correct me if I'm wrong.
Can't we write Z = 1-1+1-1+1 as this?>>>>> (1+1+1+1+1+.....) - (1+1+1+1+1+1+....) = Z
All I did was pair up the positive 1's and the negative 1's and added them together.
If you assume that both sets of sums add up to infinity, their result would come out to be zero.
But, you can also look at what the sum of 1+1+1+1.... was proved to be. Which is -1/2. So in this sense,
(-1/2) - (-1/2) = (-1/2) + (1/2) = 0. So Didn't I just prove that the sum 1-1+1-1+1.... = 0?
If not, where is my mistake?
bob5332
I think, rearranging (1-1+1-1+1-1...) as (1+1+1+1...) - (1+1+1+1...) is not valid because of the "shifting" of values, and decomposing of one infinity into two. If you insist on "proving" equality to 0 - there is an easier way: just use parenthesis like this: (1-1)+(1-1)+(1-1)... = 0 + 0 + 0 ... which is "clearly" zero. Right? Not really.
This has been bugging me all day, and the best "intuitive" explanation may be based in physics: If you draw (1-1+1-1+1-1...) on a graph assuming it's some physical value over time - it's easy to see that 1/2 is the center of oscillation. So, even though the graph never converges to 1/2 - in the infinity it may as well converge. Given the example with a light bulb.. which is ON or OFF, in the infinity, the bulb would be neither ON or OFF - it would be half-bright. If you start sequence with -1, you get an oscillating line around -1/2. So, that makes sense too. If you start doing tricks like (1-1)+(1-1)+(1-1)... = 0 + 0 + 0 ... -- it's easy to see that the trick here is selectively collapsing time intervals to 0, which doesn't make sense in the physical sense.
I started today thinking that (1-1+1-1+1-1...) = 1/2 was a fallacy, but now I think it's actually true, and it starts to make sense. However, I'm still to make the leap to understanding how (1+2+3+4+5+...) = -1/12 can be a useful fact, even if it's mathematically correct.
arash
consider the geometric series, with |x|<1:
S=1+x+x^2+x^3+...=1/(1-x)
as x goes to -1 from right, S goes to 1/2.
Stephen J Moore
the answer in numberphile is not wrong. you are only considering it in terms of finite maths axioms. when we analyze it in terms of an infinite series we do indeed get -1/12. this makes perfect sense and can be graphed. no magic need be used.
T Beaumariage
Just got home from work to have my 18 yr old son tell me about the numberphile video proof. We watched the video and I told him immediately that the false step was stating that 1-1+1-1... = 1/2. That series sum fluctuates between 0 and 1 and can never equal 1/2. The average is 1/2. Thanks for posting this article because he was falling for the magician's trick.
Mark
There is proof that 1-1+1-1+1-1....= 1/2. A simple google search will show you that this is Grandi's series and it is accepted to be 1/2. Proof is everywhere to be found. It's not a "magician's trick".