
Infinity or -1/12?
Recently a very strange result has been making the rounds. It says that when you add up all the natural numbers
1+2+3+4+...
then the answer to this sum is -1/12. The idea featured in a Numberphile video (see below), which claims to prove the result and also says that it's used all over the place in physics. People found the idea so astounding that it even made it into the New York Times. So what does this all mean?
The maths
First of all, the infinite sum of all the natural number is not equal to -1/12. You can easily convince yourself of this by tapping into your calculator the partial sums
$$S_1 = 1$$ $$S_2 = 1+2 = 3$$ $$S_3 = 1+2+3=6$$ $$S_4 = 1+2+3+4=10$$ $$...$$ $$S_n = 1+2+3+4+ ... +n,$$ and so on. The $S_n$ get larger and larger the larger $n$ gets, that is, the more natural numbers you include. In fact, you can make $S_n$ as large as you like by choosing $n$ large enough. For example, for $n=1000$ you get $$S_n = 500,500,$$ and for $n = 100,000$ you get $$S_n = 5,000,050,000.$$ This is why mathematicians say that the sum $$1+2+3+4+ ... $$ diverges to infinity. Or, to put it more loosely, that the sum is equal to infinity.

Srinivasa Ramanujan
So where does the -1/12 come from? The wrong result actually appeared in the work of the famous Indian mathematician Srinivasa Ramanujan in 1913 (see this article for more information). But Ramanujan knew what he was doing and had a reason for writing it down. He had been working on what is called the Euler zeta function. To understand what that is, first consider the infinite sum
$$S = 1+1/4+1/9+1/16+ ... .$$ You might recognise this as the sum you get when you take each natural number, square it, and then take the reciprocal: $$S = 1+1/2^2+1/3^2+1/4^2... .$$ Now this sum does not diverge. If you take the sequence of partial sums as we did above,
$$S_1 = 1$$ $$S_2 = 1+1/2^2 = 5/4=1.25$$ $$S_3 = 1+1/2^2+1/3^2 = 49/36 = 1.361...$$ $$...$$ $$S_n =1+1/2^2+1/3^2 + ... + 1/n^2,$$
then the results you get get arbitrarily close, without ever exceeding, the number $\pi^2/6 = 1.644934... .$ Mathematicians say the sum converges to $\pi^2/6$, or more loosely, that it equals $\pi^2/6.$ Now what happens when instead of raising those natural numbers in the denominator to the power of 2, you raise it to some other power $x$? It turns out that the corresponding sum $$S(x) = 1+1/2^x+1/3^x+1/4^x... $$ converges to a finite value as long as the power $x$ is a number greater than $1$. For every $x > 1$, the expression $S(x)$ has a well-defined, finite value. $S(x)$ is what's called a function, and it's called the Euler zeta function after the prolific 18th century mathematician Leonhard Euler. So far, so good. But what happens when you plug in a value of $x$ that is less than 1? For example, what if you plug in $x=-1$? Let's see. $$ S(-1) = 1+1/2^{-1}+1/3^{-1}+1/4^{-1}... $$ $$ = 1+2+3+4+ ... .$$ So you recover our original sum, which, as we know, diverges. The same is true for any other values of $x$ less than or equal to 1: the sum diverges.
Extending the Euler zeta function
As it stands the Euler zeta function S(x) is defined for real numbers x that are greater than 1. The real numbers are part of a larger family of numbers called the complex numbers. And while the real numbers correspond to all the points along an infinitely long line, the complex numbers correspond to all the points on a plane, containing the real number line. That plane is called the complex plane. Just as you can define functions that take real numbers as input you can define functions that take complex numbers as input.
One amazing thing about functions of complex numbers is that if you know the function sufficiently well for some set of inputs, then (up to some technical details) you can know the value of the function everywhere else on the complex plane. This method of extending the definition of a function is known as analytic continuation. The Euler zeta function is defined for real numbers greater than 1. Since real numbers are also complex numbers, we can regard it as a complex function and then apply analytic continuation to get a new function, defined on the whole plane but agreeing with the Euler zeta function for real numbers greater than 1. That's the Riemann zeta function.
But there is also another thing you can do. Using some high-powered mathematics (known as complex analysis, see the box) there is a way of extending the definition of the Euler zeta function to numbers $x$ less than or equal to 1 in a way that gives you finite values. In other words, there is a way of defining a new function, call it $\zeta(x),$ so that for $x>1$ $$\zeta(x) = S(x) = 1+1/2^x+1/3^x+1/4^x...,$$ and for $x\leq 1$ the function $\zeta(x)$ has well-defined, finite values. This method of extension is called analytic continuation and the new function you get is called the Riemann zeta function, after the 19th cenury mathematician Bernhard Riemann. (Making this new function give you finite values for $x \leq -1$ involves cleverly subtracting another divergent sum, so that the infinity from the first divergent sum minus the infinity from the second divergent sum gives you something finite.) OK. So now we have a function $\zeta(s)$ that agrees with Euler's zeta function $S(x)$ when you plug in values $x>1$. When you plug in values $x \leq 1$, the zeta function gives you a finite output. What value do you get when you plug $x=-1$ into the zeta function? You've guessed it: $$\zeta(-1)=-1/12.$$ If you now make the mistake of believing that $\zeta(x) = S(x)$ for $x=-1$, then you get the (wrong) expression $$S(-1) = 1+2+3+4+ ... = \zeta(-1) = -1/12.$$ This is one way of making sense of Ramanujan's mysterious expression.
The trick
So how did the people in the Numberphile video "prove" that the natural numbers all add up to -1/12? The real answer is that they didn't. Watching the video is like watching a magician and trying to spot them slipping the rabbit into the hat. Step one of the "proof" tries to persuade you of something rather silly, namely that the infinite sum $$1-1+1-1+1-....$$ is equal to $1/2.$ The video doesn't dwell long on this and seems to imply it's obvious. But let's look at it a little closer to see if it makes sense at all. Suppose that the sum $1-1+1-1+1-1....$ has a finite value and call it $Z$. Adding $Z$ to itself you get the infinite sum $$Z+Z = 1-1+1-1+1-....+1-1+1-1+1-... .$$ But this is just the original sum, implying $$Z+Z=2Z = Z.$$ Since $Z=1/2,$ it follows that $1/2=1,$ which is nonsense. So the assertion that the infinite sum $1-1+1-1+1-....$ can be taken to equal to 1/2 is not correct. In fact, you can derive all sorts of results messing around with infinite sums that diverge (see here). It's a trick!
The physics
But how did this curious, wrong result make it into a physics textbook, as shown in the video? Here is where things really get interesting. Suppose you take two conducting metallic plates and arrange them in a vacuum so that they are parallel to each other. According to classical physics, there shouldn't be any net force acting between the two plates.
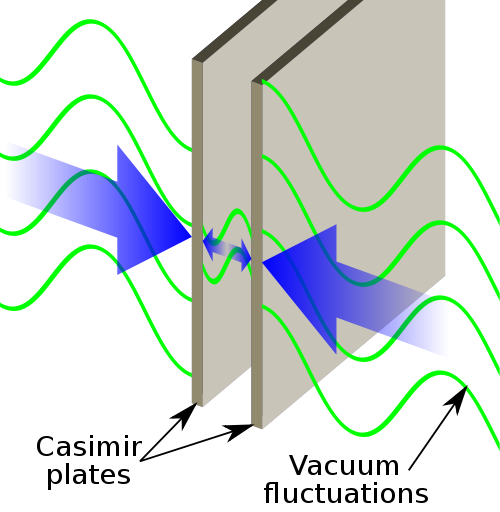
Illustration of the Casimir effect. Image: Emok.
But classical physics doesn't reckon with the weird effects you see when you look at the world at very small scales. To do that, you need quantum physics, which tells us many very strange things. One of them is that the vacuum isn't empty, but seething with activity. So-called virtual particles pop in and out of existence all the time. This activity gives a so called zero point energy: the lowest energy something can have is never zero (see here for more detail).
When you try to calculate the total energy density between the two plates using the mathematics of quantum physics, you get the infinite sum
$$1 + 8 + 27 + 64 +... .$$ This infinite sum is also what you get when you plug the value $x=-3$ into the Euler zeta function: $$S(-3) = 1 + 1/2^{-3} + 1/3^{-3} + 1/4^{-3} + ... = 1+ 8 + 27 + 64 +... .$$ That's unfortunate, because the sum diverges (it does so even quicker than than $S(-1)$), which would imply an infinite energy density. That's obviously nonsense. But what if you cheekily assume that the infinite sum equals the Riemann zeta function, rather than the Euler zeta function, evaluated at $x=-3$? Well, then you get a finite energy density. That means there should be an attractive force between the metallic plates, which also seems ludicrous, since classical physics suggests there should be no force. But here's the surprise. When physicists made the experiment they found that the force did exist — and it corresponded to an energy density exactly equal to $\zeta(-3)$!
This surprising physical result is known as the Casimir effect, after the Dutch physicist Hendrik Casimir.
Take a moment to take this in. Quantum physics says the energy density should be $$S(-3) = 1+8+27+64+... .$$ That's nonsense, but experiments show that if you (wrongly) regard this sum as the zeta function $\zeta(x)$ evaluated at $x=-3$, you get the correct answer. So it seems that nature has followed the ideas we explained above. It extended the Euler zeta function to include values for $x$ that are less than 1, by cleverly subtracting infinity, and so came up with a finite value. That's remarkable! The reason why we see $\zeta(-1)$ and $S(-1)$ in the Numberphile video and the physics textbook, rather than $\zeta(-3)$ and $S(-3),$ is that when you imagine the Casimir effect as happening in one dimension (along a line rather than in 3D), the energy density you calculate is $\zeta(-1)$ rather than $\zeta(-3)$.
So why did the Numberphile people publicise this strange "result"? They certainly know about the analytic continuation that makes the function well-defined, but that was something that was a little too technical for their video. Knowing they had the analytic continuation method, that would make the final result OK, hidden in their back pocket, they went ahead with their sleight of hand. In doing so they got over a million hits and had the world talking about zeta functions and mathematics. For this they should be congratulated. The mathematics of zeta functions is fantastic and what we described here is just the start of a long list of amazing mathematical properties. In bringing mathematics and physics to the public we always have to make choices about what we leave out and what we explain. Where to draw that line is something we all have to leave to our consciences.
About the authors

David Berman is a Reader in Theoretical Physics at Queen Mary, University of London. He previously spent time at the universities of Manchester, Brussels, Durham, Utrecht, Groningen, Jerusalem and Cambridge as well as a year at CERN in Geneva. His interests outside of physics include football, music and theatre and the arts.
Marianne Freiberger is editor of Plus.
Comments
Tristan Hubsch
The series 1-1+1-... does not converge to anything in particular, but is "summable" to 1/2 [G.H.Hardy, "Divergent series", pp.6-7]. That is to say, there exists an axiomatic framework within which the assignment of 1/2 as the sum of the series 1+1-1+1-... is unambiguous. In fact, Hardy goes on to call the (really) simple axiomatic framework (two axioms of manipulation of series—and, most importantly, which are perfectly valid for convergent series—suffice to compute a value for this series) "Pickwickian." So, it is most certainly not merely a "zeta-funciton complex analysis trick" that makes 1-1+1-... = 1/2. The point (implied, but perhaps not sufficiently emphasized by your differentiating between Euler's and Riemann's zeta function!) is that since a series such as "1-1+1-..." does not converge to anything in particular, it requires a context (an axiomatic framework) within which to acquire a meaningful value.
Ferd Berfle
While I can appreciate the desire to (and need for) stretching the frontiers of our understanding of all things, numbers included, I do think it's wrong to mess with the meaning and value of symbols like + and =, the foundation of mathematics. And infinity is not a number -- that's why it can only be described as ". . . "
1 + 2 + 3 + . . . doesn't "equal" -1/12. It has no value, other than to say "infinite," which is another way of saying we can't represent it.
Just as one can (and should) draw purple unicorns, or postulate a biology based on something other than carbon, or create any number of interesting non-Euclidean geometries, one can devise all sorts of alternative "maths" where there are different rules (where "infinity" is a number, for example), and these rules will lead to all sorts of fun conclusions, like the sum of all natural numbers equaling -1/12. These endeavors might even turn out to be useful, in some cases . . . complex numbers, for example.
But it's dishonest, unintentionally perhaps, to use familiar symbols in an attempt to present fanciful derivations as mathematical truth. And yes, there is a non-relativistic mathematical truth. And part of that truth is that you can't get a negative fraction by adding a series of positive integers.
Jérôme JEAN-CHARLES
When you say that the SIGMA of a sequence of terms 'is' V? You are ASSIGNING a value V to a sequence.
When you say "this sequence's sum is V" : this is a misuse of language!
Let's us call it an ASSIGNEMENT theory:
Each theory is suppose to obey AXIOMS ( dixit Hardy) , SUM is a function from a space of sequences on R to some (semi)ring R (i.e. N,Z,Q,R,C)
For any sequence s,s'
A1) SUM ( k.s ) = k.SUM(s) for any scalar k in R
A1) SUM ( s + s' ) = SUM(s) + SUM(s')
A3) SUM ( s shifted once) = SUM (s) - first term of s
In plain language the axioms guarantee the compatibility of SUM with adding , scalar multiplication and finite term shifting.
Examples of theory
T1) The zero theory : Any infinite sequence sums to ZERO. Obeys axioms 1,2,3
T2) The infinite theory: Any infinite sequence sums to zero if all terms are zero , else to +infinity (resp -infinity) when first non zero term is positive (respectively negative).
Obeys axioms A1 only.
T3) Classical theory : sums to V if partial sums tend to V ...Obeys axioms 1,2,3
T4) Cesaro sums ... Obeys axioms 1,2,3
T5) Ghandi sums any one that fit Axioms 1,2,3
Remark R1 : using R = N the postive integer assigning +infinity to any serie will obeys AXIOM 1,2,3
In conclusion:
Remark R2 : The contradictions shown in sum posts do not respect all axioms in their arguments.
A serie is ASSIGNED a value NOT EQUAL to that value.
CedricV
Hi,
I searched how to compute this serie.
Can you tell if the steps below are correct?
S1=1+1+1+1+...
S2=1-1+1-1+...=1/2
So
S1+S2=1+2+0+2+0+...
S1+S2-1=2+0+2+0+...
=2*S1
S1+1/2-1=2*S1
S1=-1/2
Jayanta Boral
I think there is a small mistake here.
S1+S2=2+2+2+...
So, S1+1/2=2S1 Therefore S1=+1/2
Interestingly Also S1-S2=2+2+2+...=2S1 or S1=-S2=-1/2 we get your result.
Thanks
Cedric
There is a Wikipedia page for that serie which uses analytic continuation to obtain -1/2.
S1=1+1+1+1+...
S2= 1-1+1-1+...
S1+S2= 1+2+0+2+0+...
Only sum is shifted like what is done for other series summation.
And finally for more fun:
S1=-1/2
S1/6=-1/12
So:
1/6+1/6+1/6+1/6+... = 1+2+3+4+...
Jayanta Boral
Following the Infinite Series 1-1+1-1+...til infinity = 1/2 and 1+2+3+4+...till infinity = -1/12 and applying to a series 1+1+1+....till infinity, I get a different but interesting results. I am explaining it below -
Say S=1+1+1+1+.....
I can go on adding S vertically downwards also infinitesimally but with one right shift of 1 every time, so that we get the following -
S = 1+1+1+1+1+..... till Infinity
S = 0+1+1+1+1+1+.... till Infinity
S = 0+0+1+1+1+1+1+... till infinity
.
.
.
.
till Infinity
I added 0 just to show alignment otherwise the HTML was not able to arrange numericals as I wanted.
Now adding all above, we get
S+S+S+S+....Till Infinity = 1+2+3+4+5+....till Infinity = -1/12
or, S(1+1+1+1+... till Infinity) = -1/12
or, S*S=-1/12 or S^2=-1/12 Therefore, S= Sqrt(-1/12)
So, precisely what we get is sum of 1 infinite times is square root of a negative fraction. How do we explain this?
Can anyone help?
Gabor Gulyas
Citing from Wolfram Alpha:
"Any set which can be put in a one-to-one correspondence with the natural numbers (or integers) so that a prescription can be given for identifying its members one at a time is called a countably infinite (or denumerably infinite) set. Once one countable set S is given, any other set which can be put into a one-to-one correspondence with S is also countable."
The whole proof lies on the ground of one-to-one correspondence and the definition of equality based on it.
If one accepts that |N| = |Z| (the number of natural numbers equals the number of integers) then he/she should accept the proof shown in Numberphile too - as they do the same trick again and again.
Me personally feel some controversial feeling about it and it's an open question in my mind. But if the physicists have shown that the Riemann Zeta function at -3 IS EQUAL to zeta(-3) then it suggests to me that the Cantor method is working and we can say that if we find ANY one-to-one correspondence between 2 sets that they are equally large.
However it raises other questions like how should we imagine the numbers - whether a circle would be better where the infinity and minus infinity are basically the same point on the circle just right in the opposite side from zero? It's all just very weak imagination plays but there must be something...
Anon
To be honest I think most of the critique here comes from ignoring the fact that we must apply an analytic continuation to achieve said result.
With that said, even after weeks of banging my head against a wall trying to understand it for my complex analysis class, the whole notion of analytic continuation to me is still akin to a bad acid trip.
JaapV
Your illustration that the manipulations done in the numberphile video are "tricks" by showing that 2Z = Z seems rather weak. You prove that 2Z = Z by appending the sequences to each other; an operation that is never done in the video and seems like an ill defined operation. Where would you start appending? The operations they do do: adding the elements of shifted sequences (Hilbert's hotel fashion) always provides the same unique result for a sequence in whatever way you do the manipulations, so are quite different imho.
Akki
The Grandi Series (1-1+1-1+1 . . .) was actually proved as follows:
Z=1-1+1-1+1 . . .
1-Z=1-(1-1+1-1+1 . . .)
1-Z=1-1+1-1+1-1 . . .
1-Z=Z => 2Z=1 => Z=1/2
This is perfectly true and can be used without controversy in the remaining half of the proof. Adding Z to both sides would work as an alternative proof, but it would have to be done as follows:
Z=1-1+1-1+1 . . .
Z+Z=1-1+1-1+1 . . .
+1-1+1-1 . . .
After which everything cancels out, except the 1:
2Z=1 => Z=1/2.
The way that was shown in the article wouldn't work because there is no way to know whether the second Grandi Series is being started at +1 or -1 in the original Grandi Series.
KW
I've noticed what I think is an issue with this post (I'm no mathematician though so this might be incorrect on my part). You say that Z+Z, or 1-1+1-1+1... + 1-1+1-1+1... = Z, or the original, infinite sum. When doing the math though, you end up getting Z+Z= 2-2+2-2+2..., which, according to the averaging-method used in the video to find that Z=1/2, would equal 1 since you would average 2 and 0. So Z+Z does in fact equal 2Z, or 1, and not Z, and this counters the rest of your argument about the "nonsense."
It's just my personal analysis of the explanation you gave, and as I said, I don't have too much experience in this field, so what I wrote might be completely false and I apologize if it is.
Kevin
how is it possible to add an infinite series to an already infinite series? why isn't 2Z equal to the series 2 - 2 + 2. . . ?
Anonymous
"The prolific 17th century mathematician Leonhard Euler" should be "18th century" since he lived from 1707 to 1783. "The 18th cenury mathematician Bernhard Riemann" should be "19th century".
Plamen
Euler endeed lived in the 18th century and Riemann in the 19th (and not as erroneously stated in the article the 17th and 18th). Hopefully the authors will spot your comment and correct the mistake.
This typo aside, the article is excellent and very accessible. So it is a bit puzzling to me why some readers got it wrong, missed the point that the partial sums of a diverging series do not have a limit (other than infinity in certain cases) and they even left comments trying to prove one thing or another about some finite value for this nonexistant limit. Interestingly, some readers also missed the point about the analytical extension of the zeta function and stil left comments trying to interpret -1/12 as if it were the limit of the partial sums of a series (rather than a value of the extended function). Perhaps attention to detail could have helped, like yours spotting the century count typo.
Kind regards,
Plamen
Shree
We must congratulate them for a reason. I too wouldn't get to know about zeta functions if numberphille had not made that video. I wouldn't be interested in learning about zeta functions. I read this article on watching Numberphille video. Actually, I should thank Dr David Berman. This article by him introduced me to 'zeta functions'.
Ujjwal Ranga
log(1-x)=-x-x²/2-x³/3-x⁴/4-......... for x<1
Differentiate it we get
-1/(1-x)=-1-x-x²-x³-x⁴-...... for x<1
Or
1/1-x)=1+x+x²+x³+x⁴+......
now put x=-1 we get
1/2=1-1+1-1+1-1+1-1+.........
It is true or not????
Matthew Hehir
Hi,
You remarked about them stating that the sum of 1-1+1-1+1-1 is equal to a half. This is not a mistake; however it is also not correct. There are two values for this sum, observed by putting in brackets like this: (1-1)+(1-1)... which equals 0, or like this: 1+(-1+1)+(-1+1)=1. As this apparently equals 1 and 0, some mathematicians like to speculate that the answer is in fact 1/2. Without looking at their working, I can't tell whether they approached this answer in the same way, however our lecturer did mention the fact that people do accept the answer of 1/2 when we went through this specific question.
Sayan
S=1-1+1-1+1-1+1-1+1-1+1-1+1-1+1...
S=1-(1-1+1-1+1-1+1-1+1-1+1-1+1-1+....)
S=1-S
2S=1
S=1/12
What is the error here?
Aditya04440
U just took the wrong thing and proved it wrong.....it never said z+z=z.....it said that 1-1+1-1+1-1+1-1.... infinity can either be 0 or 1 which is equiprobable which means sum will be either 0 for 1....thus using Bayes theorem it's 1/2..... It's the assumption that infinity can be made finite and can be sorted into acting like a finite number which is itself wrong
Curious and possibly deranged
I happened upon the Numberphile video being discussed here and as a non mathematician I am wondering something.
The infinite sum 1-1+1-1+1-1...
If it is an infinite series , infinite being without end.
A question : does an infinite series have a beginning?
If it is truly infinite then surely it should be written ...+1-1+1-1+1-1...
It seems the article places a forward limit on the infinite series in order to mathematically manipulate it.
Any comment would be welcome.
Also in terms of infinity , surely if a number / series is infinite , then its always infinite , and merely writing a description of it does not create the series , or build its value.
The infinite series described by 1 + 2+ 3 + 4+ 5 ...
Is this "created" by the writing of its description , or is it fully infinite and only the description is being "built" and the idea that the sum diverges is merely a guide to writing the description?
Just wondering :)
Evan Mele
Would you mind explaining how the zeta function is related to prime numbers?
holly
There is another way to show that the sum of 1-1+1-1... = 1/2, and it’s by first considering the binomial expansion of 1/(1+x), or (1+x)^-1. When you expand, you get 1-x+x²-x³..., and if you substitute in x=1, this turns into 1-1+1-1... Substitutimg x=1 into the original fraction 1/1+x which we expanded then gives us 1/2.
dandober
I found this article in the process of wondering if there were connections between free space impedance (~377ohms) and the cosmological constant(CC). I stumbled on a physics paper describing a theory of CC . In that paper two things were mentioned: The Casimir effect (CE)was mentioned as it is one experiment used to estimate the energy of free space or roughly CC. In this paper re-normalization(RN) was discussed as part of quantum theory as related to CC, etc. As described the RN method was useful in resolving infinities. I remembered how the "regularization" argument was used in the mentioned utube video on zeta(-1) = -1/12. SO I wondered if there was a connection between RN and Zeta function? I searched and found this article which referenced the CE in regards to an connection between the Zeta function and a physics problem where a infinity is encountered. SO it seems that I have found a circular path between CC, Zeta, RN and CE. Perhaps at some level they are all deeply related? It does seem evident that Zeta(-1) is stating at some level in the universe a infinite string of 1s added up wraps around and does something unexpected? Math has a funny way connecting to physics in what seems to be non nonsensical outcomes. I think in that sense zeta(-1) is closer to the truth about that series of added ones.
Anonymous
When you get into quantum physics, the result of -1/12 can be verified by all the devices you have now. Also, 1+1=10 when some math idiots get into two pigs.
eXander
You cannot that two infinite series together like that, that is just blatantly wrong.
Anonymous
Divergence does not imply that a sum cannot be analyzed, manipulated, or assigned a value. For example, the sum of Grandi's Series can be shown in numerous rigorous ways, such as Borel Summation (I personally prefer the integration method), Ramanujan summation, Euler regularization (which is roughly equivalent to Abel summation, but the latter is more rigorous because it addresses specific criticisms of Euler's method). The answer 1/2 is unique and consistent. Every method capable of summing the series will obtain the answer 1/2, and no method can obtain a different answer. There are no contradictions, only wrong answers obtained by violating rules (the common argument of grouping terms to produce 0 or 1 violates the Rearrangement Theorem and is one of the earliest known examples of the Eilenburg-Mazur Swindle).
Manipulations of divergent sums are not illegal, they are simply not strongly justified by the normal axioms of finite arithmetic. The additive identity of zero, for example, is not illegal, it just requires stronger justification. This is why it arrives at the unique, consistent answer for some divergent sums but produces contradictions in others. As a general rule, zeroes can be added in divergent sums that can be written as an equivalent Dirichlet series. Specifically, using the Dirichlet transform is the main method of zeta function regularization.
Most importantly, you cannot apply the intuition of finite arithmetic to infinite sums: even convergent ones. "You can't add positive numbers and get a negative answer" is an example of this reasoning, as is "You can't add whole numbers and get a fraction". These finite axioms can be easily shown to be irrelevant in the world of infinite sums:
1) First, a simple proof that a finite sum of rational numbers can never equal an irrational number: For any rational numbers a1, a2, a3,...an, then a1+a2+a3+...+an=(a1+a2+a3+...+an)/(a1*a2*a3*...*an). Since this number is expressible as a fraction of whole numbers, it is rational.
2) Second, a very important and powerful example that you yourself used in this article: ζ(2)=π²/6. This is an irrational number, but every term of the series ζ(2) is a rational number. If it were a finite sum, it would be impossible to obtain an irrational answer. But this sum isn't even divergent, it is convergent and well-behaved. So the breakdown of our finite rules is not because of divergence, but because we are not taking finite sums as we are used to doing.
The value of 1+2+3+4+.... is -1/12, and just because Numberphile did not explain the more complex justifications for their manipulations does not make those manipulations invalid. The result can be proven in many more difficult and abstract ways if that appeals to you more; I would recommend starting with Terence Tao's article on the subject.
Anonymous
I have seen so many articles and videos like this one, some explaining that the answer really is -1/12 and some saying it is infinity. As someone who is not the best at maths, I have no idea what the zeta function and all the other mathematical terms mean, so I cannot use my own knowledge to help. Therefore, I am still unsure as to what the answer is and would be grateful if you could let me know.
Vidyaranya Vijayapura
The article shows math is not your cup of Tea. Divergent series is not trick!
Mehul
Really great explanation never seen like this sir
Rachel
We're so glad you like the explanation Mehul, but just to clarify the article was written by David and Marianne!
Sofyan
Why we can not use ' -1/12 ' in limits?
nhfom
why did you get the infinite sum
1 + 8 + 27 + 64 +... .
???