Latitude by the stars

How do you find your way around the world? GPS? Well what if you haven't got reception? A map? Good idea, but what if you're travelling on the high seas with no land mark in sight? That's a situation that many, many people have found themselves in over the millennia. These brave seafarers used the Sun and the stars to navigate instead. And to do this, they needed a fair bit of geometry, in particular trigonometry.

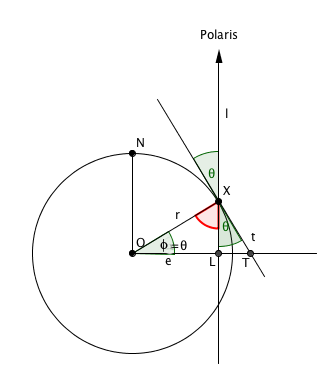
Suppose you are on the open ocean and you want to work out your latitude (see here for a definition of latitude). The Sun and most of the stars change their position in the sky over time. But some stars always appear to be in the same place. An example is Polaris, also called the North star, which always appears to be sitting directly overhead the North pole. It turns out that your latitude is the angle at which Polaris appears to sit above the horizon.

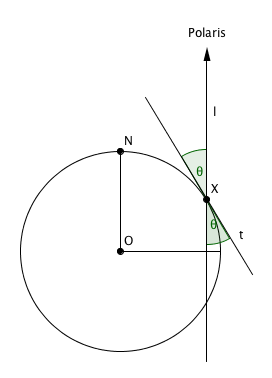
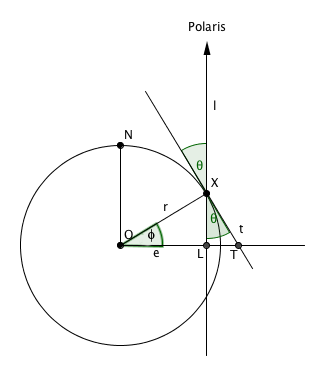
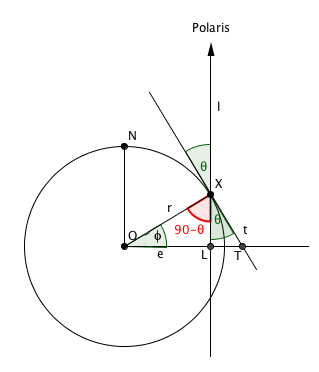
To see why, let's look at a two-dimensional picture. Consider the plane that contains the North pole, the point $X$ you are sitting at and the centre $O$ of the Earth. Strictly speaking, Polaris doesn't sit vertically above $X$, as shown in the picture, but it is so far away that the line of sight from $X$ to Polaris is very nearly vertical, so we can pretend that it does.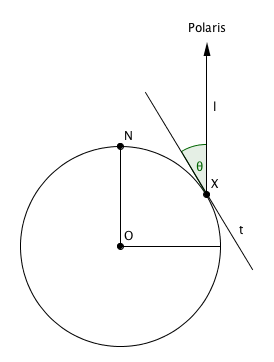 The angle that "Polaris sits above the horizon" is the angle $\theta$ indicated in the figure. It's the angle our line of sight to Polaris, call it $l$, forms with the line $t$ that is tangent to the Earth at the point $X$ (that's our line of sight towards the horizon). Extending $t$ and $l$, we see the angle $\theta$ again on the other side of the crossing point $X$: The latitude of $X$ is defined to be the angle $\phi$ that the line $r$ from $O$ to $X$ makes with the plane containing the equator. In our two-dimensional picture, that equatorial plane is just a horizontal line $e,$ which passes through $O.$ It meets the vertical line $l$ in a point $L$ and the tangent line $t$ in a point $T.$ Because $r$ is the radius of the circle and $t$ a tangent, we know that $r$ and $t$ form a right angle at $X.$ And since $t$ and $l$ form an angle $\theta,$ we know that the angle between $l$ and $r$ is $90-\theta.$ Now consider the triangle with vertices $O$, $X$ and $L.$ As we have just seen, the angle at $X$ is $90-\theta.$ Since $l$ is vertical and $e$ horizontal, the angle at $L$ is $90^\circ$. And because angles in a triangle always add up to $180^\circ$, the angle $\phi$, which is our latitude, is $$\phi = 180 - 90 - (90-\theta) = \theta.$$ Et voilà — your latitude is given by the angle $\theta$ Polaris sits above the horizon. The Greek astronomer Hipparchus defined latitude in this way over 2000 years ago. He didn't even know that the Earth was round, but our little picture here should explain why Hipparchus' definition agrees with the modern one.

There is no equivalent of Polaris in the South, but to find your latitude if you are in the Southern hemisphere you can use a constellation called the Southern cross (illustrated on the flag of Australia) and two stars called the Southern Pointers.

Over the millennia navigators have used different devices to measure the angle at which a star appears above the horizon. These include beautiful astrolabes and sextants, which you often find in antique shops and museums.

That sorts out latitude, but how do you work out your longitude? That's another story.