Scientists believe that our Universe started in the Big Bang around 13.8 billion years ago. Back then, the Universe was incredibly hot, dense, and also small. As it cooled down from the Big Bang, the Universe expanded, matter started to form and eventually clumped up into the planets, stars and galaxies we see today.

It's a remarkable fact that the distribution of matter, as well as radiation, across the cosmos was determined during the very first instant of the Universe's existence — the first fraction of a second of the Big Bang. We know this because any attempt to explain the distribution of matter from a later process necessarily requires matter and radiation moving much faster than the speed of light, which is incompatible with the laws of nature as we know them. For the past 40 years, scientists have been trying to understand the mechanism which led to matter and radiation being distributed in the way we see today.

The inflating Universe

A potential answer comes from an idea first floated in 1979 by the cosmologist Alan Guth. He suggested that for the briefest moment right at the start, the Universe expanded by an enormous amount in a short period of time. While we don't know how long this inflation phase lasted, we know that it must have been over in less than one second

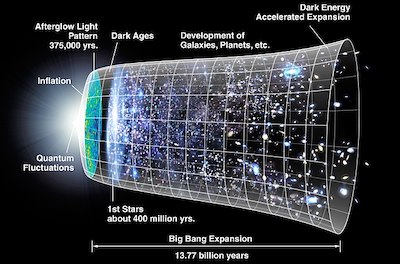
An illustration of the history of the Universe with rapid expansion (inflation) at the beginning. Image courtesy NASA.

Whatever substance was responsible for inflation is called an inflaton. It is the inflaton's distribution in space that eventually provided the seed for the distribution of radiation and matter that we observe today. Cosmologists have proposed a host of theories to explain the exact workings of inflation and many are compatible with current cosmological data. The theories are written in the language of mathematics: they are mathematical models, or models for short.

There are, however, several catches. One is that no one was around during the period of inflation to monitor what the inflaton was actually doing. We can only observe the state of the Universe at the end of inflation. When two different models agree on the final state of the Universe at the end of inflation, then we have no way of telling which model better describes reality.

Moreover, even assuming that a particular model is true, it takes serious computational power to determine the precise distribution of the inflaton that it generates. Even a crude estimate requires performing a series of incredibly complex calculations. Last, but not least, even when we do come up with an answer, it is not straightforward to extract from it general lessons that generalise to other models.

In the past few years, together with my group at the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge I have been developing an alternative approach, known as the cosmological bootstrap, to overcome the above difficulties. The aim is to derive new and more general predictions for how matter and radiation are distributed. These can then be compared to observations gathered in cosmological surveys, such as a survey that recently produced a map of the distribution of dark matter in the cosmos using data from the Atacama Cosmology Telescope in the Andes and the BOSS survey.

The main idea is to tackle the following hard question: how do we know if a given set of predictions is compatible with general principles of physics? A few examples shed light on how we have made progress on this front.

The power of randomness

One way of thinking of the inflation is as a particle, akin to the more familiar electron. When describing the word at the scale of particles, you need to resort to quantum physics. Based on quantum mechanics, the theory is famously counter-intuitive. It says, for example, that particles aren’t the point-like objects we’d naively expect them to be, but also have something of a wave about them (technically, particles like the electron or inflation are described by quantum fields).

Another prediction of quantum physics is that, at very small scales, nature is fundamentally random. For example, as long as you are not looking at it, a particle doesn't have a fixed position in space. You can't predict where you will find it when you do look — all the theory gives you are probabilities.

In mathematics, probabilities are defined to be numbers between 0 and 1: the 50-50 chance of flipping heads or tails with a coin translates to probabilities of 0.5 for each outcome. If you look at a process that can have a number of possible outcomes, such as flipping a coin, then the probabilities of the outcomes must add up to 1. That's because one of the outcomes will occur for sure.

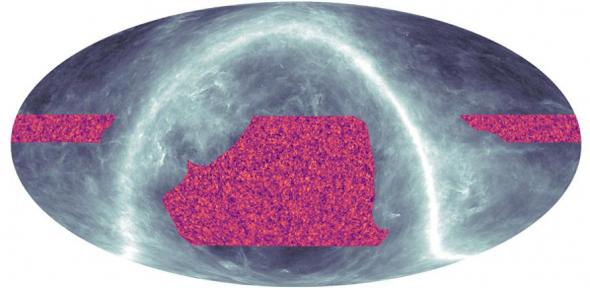
A detailed map of the dark matter in the Universe made from data from the Atacama Cosmology Telescope. (Image credit: ACT Collaboration)

These simple rules of mathematical probability theory have profound consequences in any quantum theory. This is because quantum theories derive probabilities from mathematical objects called quantum amplitudes, which are more complex than simple numbers between 0 and 1. (This is technically true: quantum amplitudes are complex, rather than real, numbers.) Demanding that quantum amplitudes combine to give meaningful probabilities leads to powerful constraints. In particle physics these constraints have been known since the 1960s and have played a key role in pretty much all developments in the field.

Because inflation relies on quantum theories, many expected similar restrictions, but nobody was able to derive them. In 2020, however, our group made a breakthrough on this problem by deriving constraints on the final distribution of matter and radiation predicted by a consistent quantum theory. This has been the starting point of much further progress on the theoretical and observational side. We were able to show in this recent work that these constraints have very concrete implications. For example, they predict that, under certain reasonable assumptions, the distribution of galaxies must be statistically indistinguishable from its mirror image. If you reflected the entire Universe in a giant mirror and then did a statistical analysis of how the galaxies are distributed, the results should be the same as for the original universe.

Cause and effect

Another cherished principle of physics, known as causality, simply states that we cannot affect the past. This restricts the ways in which a physical system can change in response to an external input: the cause must precede the effect. The restriction also translates into the mathematics describing the behaviour of the system: it turns out that only a particular class of mathematical objects, known as analytic functions, are allowed.

Remarkably, we recently proved that this powerful connection operates in the very early Universe as well. Only analytic functions can appear as predictions for the distribution of radiation and matter. This rigidity goes a long way. For example, as we showed in this recent paper, it tells us that even if we are not able to observe certain properties of the distribution of radiation and matter, we can nevertheless determine them from other data we have collected.

While much progress has taken place in just a few years, we cannot help feeling that this is just the tip of a cosmological iceberg. General properties of the predictions of inflation are yet to be revealed but can be discovered following the trail of general principles of physics. This new understanding leads directly to new signals to be searched for in the sky, and to new ways to extract information from cosmological data.

About this article

Enrico Pajer.

A version of this article first appeared in the annual report of the Kavli Institute for Cosmology at the University of Cambridge.

Enrico Pajer is a Professor of Theoretical Physics at the University of Cambridge. He has made numerous influential contributions to theoretical cosmology, and in particular its connection to quantum field theory and cosmological observables.