
Why you need maths to dance
Waves come in many different forms and affect many different aspects of our lives. Sound waves allow us to hear; visible electromagnetic waves allow us to see; radio waves allow us to communicate over long distances; microwaves allow our devices to access the internet wirelessly; X-rays and ultrasonic waves allow us to perform internal medical examinations without surgery. Our lives are endlessly shaped by waves.

Listening to music is a simple pleasure but relies on sophisticated maths.
Imagine, for a moment, being at home and playing your favourite song out loud on full volume. Shania Twain's iconic lyrics leave your speaker (everyone's favourite song is by Shania, right?) and travel as vibrations through the air to your ears. This process is well understood and relatively easy to model using high school maths.
But this is not the only path that sound waves can take from the speaker to your ears. After leaving your speaker, the sound waves radiate outwards throughout the room and are scattered by the objects and surfaces they reach. These scattered waves also radiate into the room, including travelling back towards you. This means the sound waves you hear are not only those travelling from the speaker directly to your ears, but also waves reflecting off the walls, the ceiling, the table, the lamp, your dog, and so on. This problem is a classical example of multiple wave scattering: the study of waves being scattered by multiple objects.
To understand the complex behaviour of multiple wave scattering problems, mathematicians usually begin with simplified problems problems to try and understand the fundamental behaviour. For example, imagine that you live in a minimalist home that has just a single object to scatter the sound waves. Let's say, you only have a single sofa (also, there are no walls or floors or ceilings, sorry about that). Then, there are only two paths the sound waves can take from the speaker to your ear: either travelling directly or by scattering off the sofa. That is:
$$\mbox{Sound you hear} = \mbox{sound travelling directly} + \mbox{sound scattered by the sofa}.$$
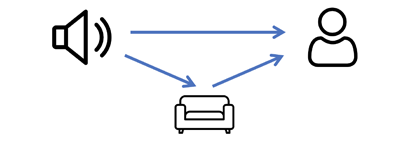
Rewording this, a general principle is: $$\mbox{Total waves} = \mbox{incoming waves} + \mbox{scattered waves}.$$
This idea can be extended to more interesting environments with multiple objects; you can have a table to go with your sofa (you're welcome). In this case, the sound waves you hear come from three places: those travelling directly to you, those scattered by the sofa and those scattered by the table.
$$\mbox{Sound you hear} = \mbox{travelling directly} + \mbox{scattered by the sofa} + \mbox{scattered by the table}.$$
The challenge, however, is that waves can reach the sofa both directly from the speaker and also by scattering off the table. That means you need to know the sounds being scattered by the table to be able to calculate the sounds being scattered by the sofa. Conversely, you also need to know the sounds being scattered by the sofa to be able to calculate the sounds being scattered by the table.
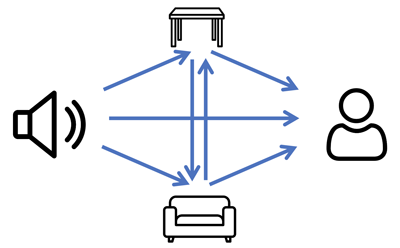
In this way, the scattering by the table and sofa are coupled. How each object scatters waves is affected by how all the other objects scatter waves. For this reason, scattering by multiple objects is substantially harder than scattering by a single object.
Once you start considering complex environments with large numbers of scatterers, a challenging mathematical problem emerges. In general, the rule is that
$$\mbox{Total waves} = \mbox{ incoming waves} + \Sigma \;\; \mbox{scattered waves from each object},$$
where the $\Sigma$ notation means you add the waves scattered from the first object to the waves scattered from the second object and the third object and so on. Each of the scattered waves depends on all the other scattered waves, giving a coupled system that requires dedicated mathematical theories to understand.
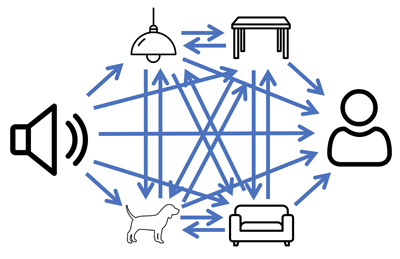
The good news is that variants of this problem have been studied by mathematicians for decades. A range of approaches for describing waves scattering by multiple objects have emerged, using techniques like integral methods and asymptotic approximations (see here for an example of such a method). One of the main challenges is calculating the waves scattered by a single complicated object. For simple objects like balls or walls this is easy enough to do, but it can be tricky for objects like tables or dogs. This is often done on a computer using methods such as finite element simulations (see here for an example of how a finite element method is used in the context of car design). Another important subtlety is that not all the wave energy will be scattered by a real object, some of it will be transmitted or absorbed. This is why, for example, some of the sound energy is able to travel through your walls into adjacent rooms, allowing your neighbours to share in your preferred choice from Shania Twain's back catalogue of pop-country feminist anthems.
Fortunately, even the intricacy of multiple wave scattering is unlikely to detract from your ability to enjoy Shania Twain’s classics in a home environment. However, problems can occur on larger scales and sound engineers need to design music venues carefully to avoid quiet spots or echoes. For example, the Victorians famously did a bad job of this when designing the Royal Albert Hall, creating an echo that would persist until sound engineers suspended 135 gigantic fibre-glass mushrooms from the ceiling in the 1960s. Nowadays, modern mathematical techniques mean that engineers can account for wave scattering in their designs and prevent these issues from occurring. The simulation below is an example of a result of such techniques. It shows how sound waves move around in the London City Hall and originally featured on Plus in our article about architecture. (Animation © Arup Acoustics.)
These considerations are not unique to sound waves; electromagnetic waves, water waves, elastic waves and seismic waves all experience similar phenomena. Fortunately, mathematical techniques allow us to manipulate and even exploit some of the exotic phenomena that can occur. Examples of this include improvements in antenna design, the development of wave energy harvesters and the creation of futuristic devices such as invisibility cloaks.
In her 1997 classic That don't impress me much, Shania Twain recites a long list of things that men have boasted to her about. Being a rocket scientist, having a car, being Brad Pitt… none of these things can impress her. But maybe, just maybe, if Shania knew the beautiful mathematics of multiple wave scattering that allowed people to enjoy her music, she’d finally be impressed.
About this article

Bryn Davies is a Marie Skłodowska-Curie Research Fellow in the Department of Mathematics at Imperial College London. He uses mathematics to develop designs for materials that interact with waves in exotic ways and are used to build devices such as waveguides, sensors and energy harvesters.
Davies is a participant of a research programme called Mathematical theory and applications of multiple wave scattering taking place at the Isaac Newton Institute for Mathematical Sciences in Cambridge. To read more content related to this programme, see here.
This article forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
