Counting the trees of life

The concept of a tree of life was popularised by Charles Darwin through his theory of evolution through natural selection. The idea is that all species evolved from a common ancestor. Evolution means that at certain points in time a species might split into two new species, which then continue to evolve on their own, perhaps splitting again at some point in the future. When you draw a picture of this you do indeed get something looking a bit like a tree (upside down in the picture below), with today's species at the ends of the branches. The problem is that given a number of species, there is more than one tree that potentially describes their relationships. For example, given three species, there are three potential trees:

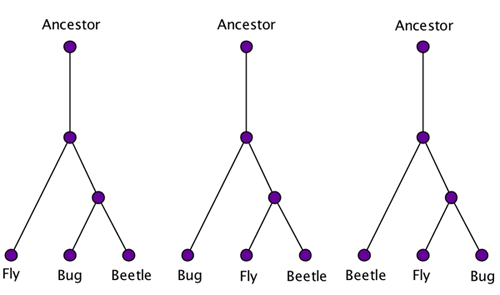
There are three different trees describing the possible genetic relationships between three species.

So here’s a question: given $n$ species, how many different possible trees of life are there?

We can answer this by doing a bit of counting. First of all, let’s be clear about what kind of object we are counting. We’ll assume that a tree of life looks something like the picture below. There is a root which represents the common ancestor. We assume that species can split into at most two (not three or more) other species at a time. Such trees are essentially what mathematicians call rooted binary trees. The tips of the branches, which represent the species alive today, are called the leaves of the tree. A line segment in the tree that connects two neighbouring branching points, or a branching point and a leaf, is called an edge.

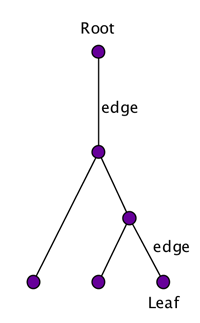
This is a rooted binary tree. (Strictly speaking, a rooted binary tree has two edges attached to the root, rather than one, but that distinction is not really important here.)

It’s not too hard to convince yourself that a rooted binary tree with $n$ leaves has a total of $2n-1$ edges. You can do this by playing around with a few of these trees, or, much better, by using a proof by induction. A binary rooted tree with $n=2$ leaves obviously has $3$ edges. And since $2n-1$ equals $3$ for $n=2$ this fits the bill.

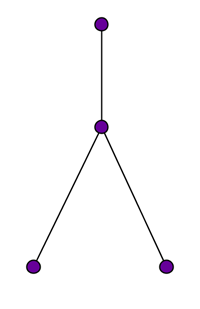
A rooted binary tree with two leaves has three edges.

Now suppose the claim holds for any rooted binary tree with $n-1$ leaves. That is, any rooted binary tree with $n-1$ leaves has $2(n-1)-1 = 2n-3$ edges. Now any rooted binary tree with $n$ leaves can be created from one with $n-1$ leaves by picking an existing edge, dividing it in half by a new branch point and have the new leaf sitting on the end of a new edge emanating from the new branch point.

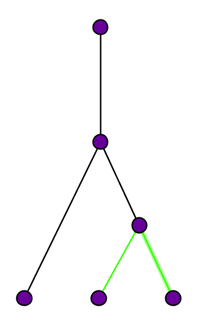
Here a rooted binary tree with three leaves has been created from one with two leaves by dividing an edge into two (a green and a black segment) and attaching the leaf to the end of an edge (green) that emanates from the new branch point.

This procedure creates two new edges that weren’t there before. So if, by our induction assumption, the tree with $n-1$ leaves had $2n-3$ edges, then the tree with $n$ leaves has $2n-3+2 = 2n-1$ edges. This proves the fact that any rooted binary tree with $n$ leaves has $2n-1$ edges.

How does that help us count the number of trees with $n$ leaves? Well, first of all notice that if $N_1$ is the number of trees with $n-1$ leaves, then the number of trees with $n$ leaves is $(2n-3)N_1.$ That’s because, as we have already seen above, a tree with $n$ leaves can be made from one with $n-1$ leaves by attaching the new leaf to one of the existing $2(n-1)-1=2n-3$ edges. So for every rooted binary tree with $n-1$ leaves there are $2n-3$ rooted binary trees with $n$ leaves: one for every edge of the first tree.

But what is the number $N_1$ of rooted binary trees with $n-1$ leaves? Well, we can make a rooted binary tree with $n-1$ leaves out of one with $n-2$ leaves, just as we made a tree with $n$ leaves out of one with $n-1$ leaves. Now, a rooted binary tree with $n-2$ leaves has $2$ fewer edges than a rooted binary tree with $n-1$ leaves. Since a new leaf is attached to one of the edges, we can therefore make two fewer trees with $n-1$ leaves out of trees with $n-2$ leaves than we can make trees with $n$ leaves out of trees with $n-1$ leaves. Writing $N_2$ for the number of trees with $n-2$ leaves, there therefore are

$N_1=(2n-3-2)N_2 = (2n-5)N_2$

trees with $n-1$ leaves.

Similarly, writing $N_3$ for the number of trees with $n-3$ leaves, we see that

$N_2 = (2n-5-2)N_4 = (2n - 7)N_3.$

You might be able to see where this is going. Working your way backwards, the number $N_0$ of trees with $n$ leaves is

$N_0 = (2n-3)(2n-5)(2n-7)(2n-9)\times ... \times 3 \times 1.$

This expression is often written as the double factorial

$(2n-3)!! = (2n-3)(2n-5)(2n-7)(2n-9) \times ... \times 3 \times 1.$

It grows very quickly with $n.$ For $n=3$ there are

$3 \times 1 = 3$

rooted binary trees.

For $n=10$ there are $34,459,425$ rooted binary trees. And for $n=20$ there are $8,200,794,532,637,891,559,375$ rooted binary trees. That’s one of the problems facing people who study evolution. Even for a small number of species there is a huge number of potential trees describing their potential relationships.

You can read more about the maths of trees of life in Reconstructing the tree of life and Evolution: It's as real as gravity.

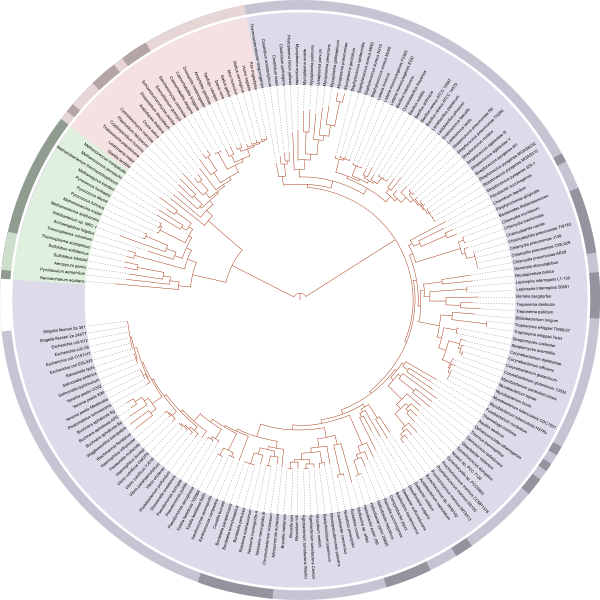
A tree of life, showing the relationship between species whose genomes had been sequenced as of 2006. The very centre represents the last universal ancestor of all life on earth. The different colors represent the three domains of life: pink represents eukaryota (animals, plants and fungi); blue represents bacteria; and green represents archaea. Note the presence of homo sapiens (humans) second from the rightmost edge of the pink segment. Click here to see a larger version of this picture.

Comments

At the point when a tree has

At the point when a tree has been chopped down or felled, then it is moderately simple to work out its age by checking the development or yearly rings that can be seen on the sawn-off stump. Under the bark of a tree is a unique tissue (called the cambium) which frames new cells so that the tree can develop.

Contrasts in the rate at which cells are delivered by this tissue offer ascent to the yearly or development rings. On the off chance that conditions are useful for development (warm, general precipitation) then the ring that is shaped will be more extensive than that made in a year where the tree battles for water, or it is cool. There is one ring for every year of a tree's life. http://www.vue8residences.sg

Eats roots and leaves

This article, and and "Reconstructing the Tree of Life", inspired me to construct Fibonacci and Lucas rooted binary trees along with their distance matrices. For Fibonacci start off with a root A, representing a species if you like or an individual organism. From it emanate two leaves B and C. In turn B gives rise to two new leaves, D and E, but from C only emanates one, F. So three leaves emerge at this stage. From D emanates two new leaves, G and H; from E only one, namely I; but from F also emanate two, J and K. So five leaves at this stage. And so on. The general rule is that if a given leaf X only produces one leaf then that daughter leaf must go on to produce two, but if X produces two, then only one of those can itself can produce two and the other just one. This rule also applies to Lucas except that we begin with two roots which fuse into one leaf, which in turn splits into three. Of those three, one produces two leaves, but the other two only one each - so four altogether. This could model the numerical difference some kind of sexual (individual or inter-species) reproduction makes. In both cases we can have the species or individual die out after its act of evolution or reproduction, or remain in existence, as the numbers given only refer to new leaves.

Some very interesting distance matrices emerge. In my version of the Fibonacci, it's B followed by A which has the lowest value by my reckoning if we assume a value of 1 for every edge.