Maths in a minute: Maths and music
Growing up playing musical instruments and also enjoying maths at school, I was often told by music teachers, maths teachers and family members that these subjects were related. I always accepted this link but never understood just how many connections there were between the subjects, so I decided to find out!
What is a note?
Sound is produced by something in an instrument vibrating (a string, a reed, a drumskin, etc) which causes nearby air particles to vibrate too. These particles cause further neighbouring particles to vibrate, and collectively make up a sound wave. The ear then hears a sound when these vibrating particles cause the eardrum to vibrate.
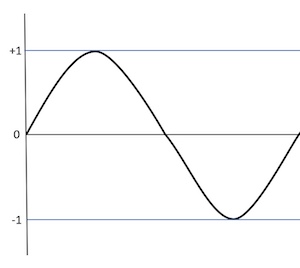
A complete wave cycle
The instrument is vibrating at a certain frequency, which means the number of wave cycles per second, measured in Hertz (Hz). The higher the frequency the higher the pitch of the note. For example, the note A4 (the A above middle C) has a frequency of 440 Hz, meaning the instrument is vibrating 440 times per second. A note an octave above has a frequency of twice the original note.
Why do different instruments sound different?
If we play the same note on two different instruments it will sound very different. But why is this the case? We're playing the same note – making sound waves with the same frequency – so why doesn't it sound the same?
Let's look at different instruments playing the note A4. The secret is that when any instrument is playing this A, which we call the fundamental frequency, the instrument is also vibrating at harmonic frequencies, which are exact multiples of the fundamental frequency. For this A, the second harmonic is 2 x 440 = 880 Hz, the third harmonic is 3 x 440 = 1320 Hz, and so on. Different instruments produce these harmonics at different volumes compared to the fundamental frequency of that note, which is what gives them a unique sound. The frequencies will all be the same, but each instrument combines them uniquely.
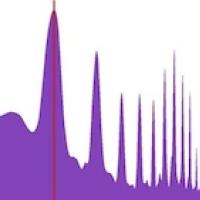
Here's an example of the harmonic frequencies produced by the note A4 on piano and acoustic guitar, which I produced on a piece of software called Audacity.

The frequencies produced by a piano on the left, and a guitar on the right. The frequencies of the sounds produced are measured in Hertz along the horizontal axis. The vertical axis represents how intense (or loud) the sound is, measured in decibels.
The fundamental frequency of 440Hz is marked by a vertical line on each graph. This looks similar on both graphs, and after that you can see the harmonic frequencies at 880 Hz, 1320 Hz, 1760 Hz and so on. Both graphs have peaks at the same values, however the height of the peaks varies which is what makes a piano and guitar sound different.
Why do harmonies sound nice to us?
Now if we were to play two different notes at the same time, some pairs of notes would sound "nice" to us, and some would clash. What dictates which combinations sound good together?
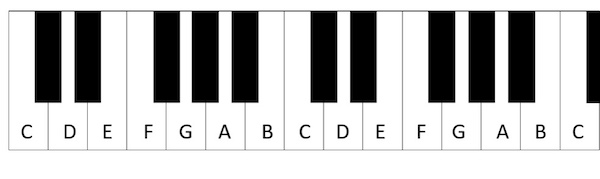
Two notes labelled with the same letter are an octave apart. Starting from C, the G above it is a fifth apart, and the F above it is a fourth apart. An example of a tritone is from C to F♯, the black note to the right of F.
Let's first look at if we were to play notes an octave apart, which sounds nice to us. The frequency of the higher note will be twice that of the lower note, and so the simplified ratio between the frequency of the two notes is 1:2. These are simple numbers, and this corresponds to us finding the sound pleasant.
The same is true if you play notes a fifth apart (see the figure above): the ratio of frequencies is 2:3, and notes a fourth apart give a ratio 3:4. These are also small, simple numbers. However, if we were to play notes a tritone (six semitones) apart the resultant ratio is 45:32 which is made up of larger, more complicated numbers and so the notes in this interval clash.
Tuning
Historically, instruments were often tuned using a method called just tuning, which creates different intervals using whole number ratios. An example of this is Pythagorean tuning (attributed to Pythagoras in the 6th century BC), where intervals of a perfect fifth (which uses the ratio 3:2) are stacked to tune each note to be a fifth above the previous note.
A system like this works well for music written in a particular key with few sharps or flats, however issues arise when transposing music to a key with a higher number of sharps or flats because the intervals used are different in the different keys, resulting in the music sounding out of tune. Just tuning is still used with instruments like the bagpipe as it always stays in one key, and bagpipes are rarely played with other instruments so their different tuning doesn't cause issues.
In the 16th century a new style of tuning was calculated called equal temperament, which splits the octave into equal steps. This is what is now typically used in classical and western music, where we divide an octave into 12 semitones of equal size. Modern Arab tuning also uses equal temperament but divides the octave into 24 instead of 12. This method of tuning makes it easier for keyboards and other instruments to play in all keys, and so replaced just tuning.
If we look back at the 12-tone equal temperament, the frequency of each semitone step increases by a factor of the twelfth root of 2, which is approximately 1.06. So a semitone above the A4 we looked at before (with a frequency of 440 Hz) has a frequency of (440)x21/12= 466 Hz. To find a semitone above, we multiply this answer again by 21/12. If we were to do this 12 times in total, we would reach the note A, an octave above our original A4. This means that the octave above, the 12th semitone, has a frequency of two times that of the original note.
This multiplicative structure is essential to ensure that every octave is made up of the same number of notes. For example, we know the notes with frequencies 100 Hz and 200 Hz are an octave apart. We could use an additive method to create a five note scale between these two notes, with frequencies increasing by 20 Hz each time. However, if we then tried to use this 20 Hz increase between another octave, say from frequencies 400 Hz and 800 Hz, this would lead to having 20 notes in this octave. This would mean that certain notes would only exist for higher voices or instruments, as they would have more notes available to them to use. Using a multiplicative method instead puts notes appropriately in each octave.
These are just a few of the examples of how maths appears in music, there are many more fascinating connections that you could research further!
You can find out more about the connections between mathematics and music on Plus!
- You can read more on how we hear sound and music, and what makes an object musical in The magical mathematics of music and What makes an object into a musical instrument?
- You can find out more about the role of harmonics in music and the maths behind them in The music of the primes and Why is the violin so hard to play?
- You can hear more about how notes sounds different on different instruments, and why some notes go together so well in this podcast tour of La La Lab exhibition.
- You can find out more about the maths behind tuning and musical scales in these Music and Euclid's algorithm, Sine language and The magical mathematics of music.
About this article

Kate Stansfield recently graduated from the University of Bath with a degree in Mathematical Sciences, and is now training to be a secondary maths teacher. She's always had an interest in music, growing up learning the piano, violin and viola, and really enjoyed researching the links between these subjects.
This content now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
wadee milhem
This is a valuable issue, it is clear that the writer is found of music, I am so glad to recognize to your wonderful site,
I have the same interests that you interest,
I will tell you that I have a motivating research about mathematics and music and I will have the honor to assist my research,
wadee milhem
Syria