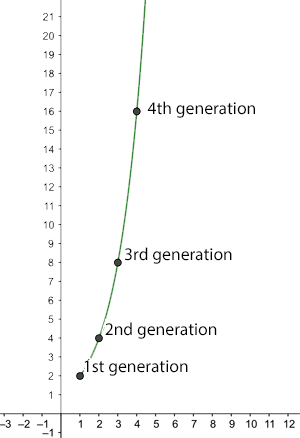
The number of new infections after n generations for R0=2.
Two things many of us will have heard about over the last few weeks are the concept of herd immunity and a number called (which people say as "R nought").
The basic reproduction number
Given an infectious disease, such as COVID-19, is the basic reproduction number of the disease: the average number of people an infected person goes on to infect, given that everyone in the population is susceptible to the disease. For COVID-19 this is currently estimated to lie between 2 and 2.5. For seasonal strains of flu, it lies between 0.9 and 2.1. And for measles it is a whopping 12 to 18.
You can see how a large enough leads to a rapid spread of the disease. For example, if is equal to 2 then a single infected person generates the following growth of new infections:
1st generation: new infections
2nd generation: new infections
3rd generation: new infections
4th generation: new infections.
Generally, there are new infections in the th round of new infections. Assuming a person is only infectious for a week, at this rate the entire world population (7.8 billion) would be infected after slightly over 32 weeks.
When the basic reproduction number is less than 1 a very different picture emerges. As an illustration, imagine we have Now obviously, an infected person can't go on to infect half a person, but remember that this is an average: it means that 10 people can be assumed to go on to infect 5 others, or that 100 people can be assumed to go on to infect 50 others. As before let's assume there is 1 infected person to start with, then the number of new infections behaves like this:
1st generation: new infections
2nd generation: new infections
3rd generation: new infections
4th generation: new infections.
Generally, there are new infections in the th round of infections. This number becomes smaller and smaller as the number of generations becomes larger. A dead end for the disease.
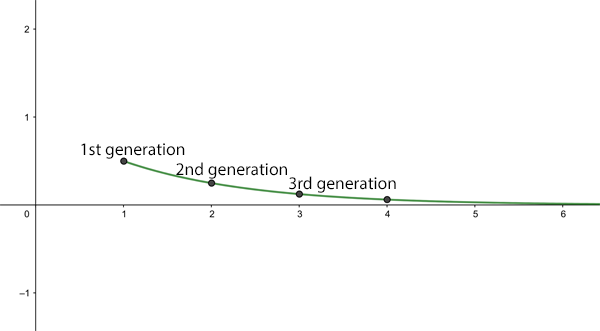
The average number of new infections after n generations for R0=0.5.
What if ? In this case the disease will be endemic: always present in the population, but not an epidemic.
See here for all our coverage of the COVID-19 pandemic.
The effective reproduction number
So, given that the of measles, or some strains of seasonal flu, is greater than 1, how come the whole world hasn't been infected with these diseases a long time ago? The reason is that
is the average number of people an infected person goes on to infect, given that everyone in the population is susceptible. In real life, this might be the case if someone who has become infected with a disease elsewhere enters a part of the world where the disease has never been seen before, so people don't have immunity and there isn't a vaccine to protect them. An of then means that, at the beginning, the number of infected people will grow wildly, as we've described above.
However, once a person has recovered from the disease they will (hopefully) gain some immunity. This means that after a while we're not dealing with a totally susceptible population anymore. Indeed, there may be other reasons why some people in the population aren't susceptible: they may be immune for other reasons, or if there's a vaccine, they may have received it, or they may be isolated from the rest of the population.
In most real life situations we should be looking at the effective reproduction number of the disease, sometimes denoted by : the average number an infected person goes on to infect in a population where some people are immune (or some other interventions are in place). Of course and are related. Writing for the proportion of the population that is susceptible to catching the disease, we have
As an example, if only half the population is susceptible, so , we have . In this case, if is less than or equal to , then is less than or equal to and the disease won't turn into an epidemic. The ideal aim of any intervention, be it vaccination or social distancing, is to get the effective reproduction number down to under 1.
Herd immunity
What does all this have to do with herd immunity? The general idea behind herd immunity is that in a population where many people are immune a disease can't take hold and grow into an epidemic, thereby protecting people who aren't immune. The population (perhaps unfortunately called a herd ) protects vulnerable individuals.
So how many people in a population need to be immune to have herd immunity? Imagine a disease has a basic reproduction number , which is greater than 1 so an epidemic threatens. As we have seen, if the effective reproduction number is less than 1, then the disease will eventually fizzle out. So to achieve herd immunity we need to somehow get the effective reproduction number to under 1. Since , where is the proportion of the population that is susceptible, we need
Rearranging, this gives
In other words, we need to get the proportion of susceptible people in the population to under How many people need to be immune to achieve this? If the proportion of susceptible people is , then the proportion of people who are not susceptible, in other words immune, is . Now
means
So, to achieve herd immunity we need to make sure that at least a proportion of of the population is immune. For an of 2.5, the higher end of the estimates for COVID-19, this means that we need to get at least a proportion of of the population immune. This translates to at least 60\%.

The herd can protect the individual.
How do we do this? Well, ideally we would do it by vaccinating at least 60% of the population. In the absence of a vaccine, we can hope that this level of immunity will be achieved naturally, by people becoming sick and then immune. But because a lot of people die of COVID-19 we can't just let the disease wash over the population, confident in the knowledge that more infections mean more immunity.
It's because we need to protect vulnerable people and our health care systems that much of the world is currently in lockdown. Ironically, lockdowns mean that many of us are not gaining immunity by having been infected, so the epidemic may spike again once social distancing measures are lifted.
So what are we to do in this worst case scenario? One option would be to remain in lockdown until there is a vaccine, but that could be over a year. Another is to go into intermitted lockdowns to keep successive spikes of the epidemic below the critical capacity of health care systems.
The truth is that at this moment nobody knows exactly what is going to happen in the future. Our most educated guesses come from mathematical models which try and predict the course of the pandemic. You can find out more about these models here. An urgent call has gone out to the scientific modelling community to help find the best exit strategies from our current predicament.
In general, our calculations above also send an important message about vaccination: it does not only protect the individual who is being vaccinated against the disease, but also those people who for some reason or other won't be vaccinated and are therefore vulnerable. Vaccination isn't just for you, it's for the whole "herd"!
This article is based on a chapter from the book Understanding numbers by the Plus Editors Rachel Thomas and Marianne Freiberger.




Comments
David C Brown
This article by Marianne Freiberger is by far the clearest and most illuminating introductions I have read in my quest to understand the mathematical modelling of the spread of the Covid-19 disease. I now feel more confident in reading more detailed articles, such as those describing SIR models.
David Passmore
How is "crowd immunity" calculated when R0 < 1?
Thanks
Marianne
When R_0<1 you already have herd immunity from the outset.
Tatjana
When R0<1 it doesn't mean you have "herd immunity from the outset", it just means the virus has a reproductive rate less than 1.
peter acworth
The two statements are interchangeable... The very definition of 'herd immunity' as used in this article is that R (effective Replication rate) is <1. If R0<1 you have R<1 even when the entire population is susceptible.
Dustin
Yes, when you have R0 < 1 you have herd immunity. If the same disease had R0 > 1 with one population and R0 < 1 with another population, the first population would get sick and the second would be herd immune. A disease can have different R values in different populations. In a society were everyone wears face masks if they have so much of a sniffle and another population that coughs in restaurants without covering their mouth, the R value in mask wearing population is going to be much lower, which is why S. Korea did so well with Covid. If the R val of a disease is less than 1 for all populations, the disease goes extinct.
james monteith
Kinda obvious really isn't it. You wouldn't have herd immunity if a new strain was more contagious and only 3 people had been exposed the first time. The use of the word herd does suggest it is the number of people infected rather than interchangeable any reasons for it to die out
Ed Gracely
Very good article, thank you!
My thinking is that even with a vaccine we may need to retain some limited degree of social distancing. 60% immune is a lot unless we get a vaccine more effective than for flu and a very high percentage taking it. BUT if a modest amount of social distancing (maybe avoid really big crowds, keep a distance when reasonable...) plus extra hand washing, will reduce the reproductive number to, say, 1.5, then we only need 33% immune -- that's more attainable.
IanM
R=sR_0. So the effective reproduction number is a simple linear multiple of R_0, scaled by the proportion of people who are susceptible.
Imagine a scenario where a population is 100% susceptible. (s=0) One member is infected. Infection lasts a week. During each week, the infected person has contact with 2 other people. Each contact has a 50% chance of passing on the infection. So the chance of *not* infecting anyone during the week is (1-0.5)^2, or 25%. Thus, the chance of infecting someone is 100%-25% = 75%.
Now, imagine the same scenario, except that there is 50% herd immunity. (s=0.5). So in the same story, one of those two people was immune. So they only had a 50% chance of infecting someone.
Comparing s=0 with s=0.5, we see the chance of spreading the infection change from 75% to 50%. Oops. According to R=sR_0, we expected it to go from 75% down to 75%/2 = 37.5%.
Spot my error! :)
inno
In your first scenario, the chance of infecting someone is 75%, that is true. However, the probability of infecting two people also exist, at 25%. The mean number of infection is 50% * 2 = 1, thus r0 = 1.
What is important about calculation of r0 is not whether you infect someone, but the number of people you infect. Why do we say when r0 < 1 we have herd immunity? It means that if one person on average infect less than 1 person in the duration then eventually the disease will stop spreading.
CHRISTOPHER EATON
I think I understand the concept of Ro. If I have the virus then it will be expected that I will infect a certain number of people. My question is this: what is the percentage of people I meet that will be infected. Obviously, if I meet no one, then I infect no one. What if I meet 10 people? 20 people...100 people...1,000 people etc etc.
Alex Ferguson
Obviously this depends on what sort of "meeting" is involved. A brief conversation 4m apart in the park is going to be rather different from a weekend of... especially close indoor contact, as it were.
Basically the R-0 is a virological *and behavioural* average. The average person shedding the average viral load interacting with others in the average way will infect R-0 others. How many meetings (and of what sort) that is you'd have to ask the behavioural modellers...
Phil Thompson
Given we have a small proportion of deaths in the under-40s (<10% of total) and in under 20s practically zero deaths or serious cases I started to think about the "not susceptible" as distinct from the immune. If 40% of the population are barely touched by the disease do we only need 20% with acquired immunity to get us over the 60% line of non-susceptible people ?
Kinga
No because to have herd immunity you must not be able to pass the disease on to others. It’s not enough that you only get a mild form of the disease. If you can pass it on, you’re useless for the purposes of herd immunity.
Alex Ferguson
Arguably worse than useless from a population immunity point of view, as people who feel at no personal risk whatsoever may well engage in riskier behaviour, thereby pushing the effect R-number back up.
Gita Das
This article is by far the best in explaining the basics of Reproduction number (both basic and effective) and herd immunity.
Rich
The article mention vaccinating 60% of the population to obtain heard immunity for a R0 of 2.5. Doesn't that make the supposition the vaccine is 100% effective? Shouldn't we say for example the vaccine is effective at 75% that 80% of the population would need to be vaccinated?
John-H
I would think so - if a vaccine was 70% effective then if you vaccinate 100 people you'd expect 30% could become infected despite being vaccinated which is the same result as vaccinating 70 people with a 100% effective vaccine.
This is particularly concerning with the new 202012/01 strain being relatively 1.74 times more transmissible. If the original Corona virus had a natural R0 = 3 , 1 - 1/R0 = 0.66 i.e. 66% requirement of population to be vaccinated to achieve herd immunity, then with the new variant R0 = 5.22 the same calculation works out to 80% of population and won't be achieved with a 70% effective vaccine.
drgpoppy
This fails to consider if the vaccine is less effective you have faster natural infection that increases herd immunity per period of time. The R0 at 2 in a fully susceptible population if you remember from the original article says if the R0 was 2 as everyone said, the entire world would be infected within 32 weeks which didn't happen. The R0 therefore can't be a 3 and having a new variant more virulent than the R0 of 2 is immaterial to the spread.
Marianne
The calculation assumes the vaccine is 1005 effective and that it stops transmission. for a calculation involving a less effective vaccine see here https://plus.maths.org/content/herd-immunity-will-protect-us-all-why-do…
Malcolm Holmes
With reference to Adam Kucharski's book the Rules of Contagion (page 58) formulates that R is a function of Duration of infection, Opportunities to spread, Transmission probability and Susceptibility. This appears to be reasonable however with a little thought it can be seen that a clear definition needs to be given to each. For example the transmission probability is likely to vary depending on the nature of the opportunity face to face indoors, face to face outdoors, infection left on a surface etc. All the variables in the DOTS function are incredibly difficult to establish accurately (using either real or modelled data). Since the Ro value is similarly constrained it is difficult to see how it is so accurately reported. In real life statistics would be used to try and obtain acceptable values. The current COVID testing data does not seem to imply that we have enough meaningful data to do this. I assume that if we had a reliable source of up to date data the R value could be calculated, but this does not appear to be the case. It is not in the Scientific interest to pretend that Science can always be the saviour. Again to reference Adam Krucharski's book (page 154) 'According to Chris Whitty, now Their Medical Officer for England, the best mathematical models are not necessarily the ones that try to make the most accurate forecast about the future. What matters is having analysis that can reveal gaps in our understanding of a situation. 'They are generally most useful when they identify impacts of policy decisions which are not predictable by commonsense,' Whitty has suggested. 'The key is usually not that they are "right", but that they provide an unpredicted insight. I have worked in the modelling environment in the Aircraft industry and have seen FEM models used successfully however I have also seen models that can only predict very simple senerios.
Bob Pearsall
Herd immunity is an unfortunate term of art that has become well established in the lexicon. Something along the lines of herd attenuation is more helpful and accurate. However, changing this will be as difficult as changing the gobsmackingly awful grinding of English to dust here in the USA, where we are changing the meanings of enormity, literally, unprecedented, and where we are oblivious to the necessity of the final comma in a list.
m.
In my country there was a vaccination campaign, people got divided into vaccinated /unvaccinated and government publicly said that vaccinated people are not spreading the infection, only unvaccinated are to blame for that. I have gathered all the data about people infected here, turns out vaccination campaign raised the spread of covid (nobody calculated Re or Rt here at all, they looked only at the number of infected people).
I'm a lawyer and i want to take my government to court for that, as many lost their jobs, got infected and died because of that. The information here is perfect, but the book mentioned - "Understanding numbers" might not be considered good enough proof for that - maybe someone can pinpoint any medical journals with the same information? Or maybe help with formulating a reference to this site correctly, as the connection to University of Cambridge is clear for me, but might not be clear for the judges where I live (they lack experience in evaluating evidence past 2, 3 years at least e.g. water condensate forms at 80% air humidity, according to high court).