
Meet the gyroid
What do butterflies, ketchup, microcellular structures, and plastics have in common? It's a curious minimal surface called the gyroid.
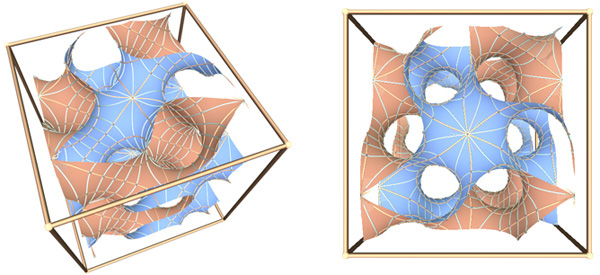
Figure 1: Two views of a section of the gyroid surface.
Scientists and mathematicians have long studied soap films and bubbles. Soap film takes the shape it does, in part, because the surface tension and the pressure of air on both sides of the film cause the film to want to take the minimum amount of surface area necessary to span a region of space. A minimal surface is a mathematical model of a soap film — a simplified version that ignores the effects of gravity and some other physical phenomena.
The mathematical definition of a minimal surface $M$ goes as follows. Take any point $p$ on $M$ and consider small spheres centred at $p$. Each sphere will intersect $M$ in a curve. Then $M$ is a minimal surface if for at least one of the spheres, call it $S$, the part of $M$ that lies inside $S$ has the smallest possible area of all surfaces which contain this curve (see figure 2). This has to be true for all points $p$ on $M$.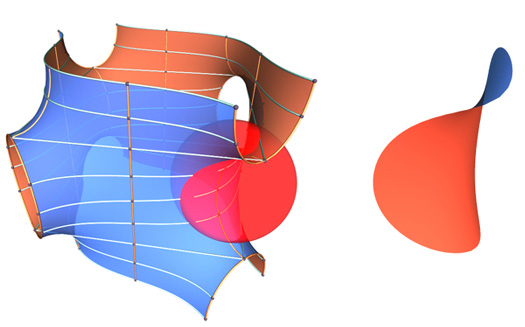
Figure 2: A small sphere intersected with a minimal surface, and the piece of the surface lying inside the sphere. The small piece has the smallest area among all surfaces with the same boundary.
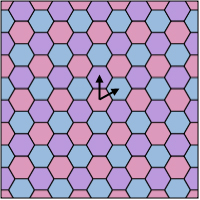
Figure 3: The honeycomb lattice. The arrows indicate the vectors that generate the lattice.
The study of minimal surfaces began as early as the mid-1700s, but the golden age of minimal surfaces was in the mid to late 1800s, when Joseph Plateau (who was blind from staring directly at the sun for 25 seconds for an experiment), Hermann Schwarz, and others studied minimal surfaces and made great advances. After a long dormant period, Alan Schoen (a U.S. National Aeronautics and Space Administration scientist studying super-strong, super-light structures) discovered the gyroid in 1970.
To start to understand the geometry of the gyroid, let's consider a more familiar example: the honeycomb lattice in the plane (see figure 3). This arrangement of hexagons is doubly periodic; there are two vectors v and w that generate the lattice. In other words, if you start with a single hexagon and translate copies in the directions of v and w, you can generate as large a piece of the lattice as you wish. Another way of saying this is that the lattice is invariant under translations of v and w; if we translate a copy of the entire lattice by v or w, the copy will be perfectly superimposed on the original lattice.
The gyroid has a similar structure. It is triply periodic, meaning that a small piece of the surface may be used to assemble the entire surface by taking a fundamental piece and translating copies in three independent directions in space (see figure 4).

Figure 4: A translational fundamental domain of the gyroid surface. By translating this piece in three independent direction of space, we can assemble the whole surface.
The mathematical equation that describes the gyroid is complicated, involving elliptic integrals. However, rather amazingly the trigonometric equation $$\cos{x}\sin{y}+\cos{y}\sin{z}+\cos{z}\sin{x}=0.$$ gives an approximation to the gyroid surface that looks to the eye quite a bit like the actual gyroid.
Many examples of triply periodic minimal surfaces were known prior to Schoen's work, but all examples had been constructed by thinking of a particular nice boundary curve and then finding the equation describing the soap film you'd get by dipping a wire frame shaped like the curve in soap solution. To make the surface repeat in space, these wire frames were constructed of straight lines, with "nice" angles, and the surface was then formed by rotating about these lines and reflecting in planes. For example, the CLP surface has a wire frame shown in figure 5.
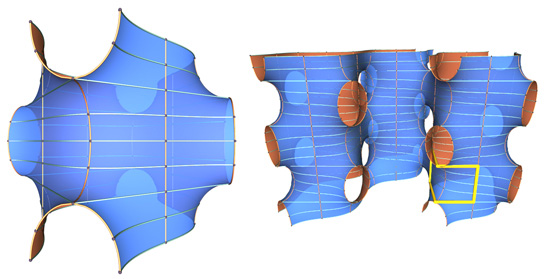
Figure 5: A fundamental domain of the CLP surface, with a wire-frame highlighted in yellow (left). Several copies of the fundamental domain (right).
What is special about the gyroid is that it has no planes of reflectional symmetry and no straight line segments lying on its surface. This makes the surface much more difficult to visualise.
But what really makes the gyroid interesting is that it seems to appear in all sorts of natural places! The force of air on two sides of a membrane results in a kind of competition; if there were no air beneath the surface then the air on top would push the surface down and vice versa, so a minimal surface is an equilibrium position. This same competition occurs in other places in nature, and that may be why minimal surfaces are frequently observed by scientists.

An image of a gyroid created by Bathsheba Grossman.
Scientists recently announced in the Proceeding of the National Academy of Sciences that the beautiful iridescent colors in butterfly wings are caused by gyroids made of chitin and air.
In another study a team of scientists used transmission electron microscopy to study the membranes inside biological cell components called mitochondria. These are the cell's power plants, converting energy into a form that is usable by the cell. Here too scientists found surfaces that appear to be the gyroid.
A third team of scientists is using a giant, distributed supercomputer to study how highly viscous liquids like ketchup flow. In these liquids, the competition of amphiphilic (both water-attracting and fat-attracting) molecules results in a certain kind of molecular tension or competition; there too scientists are finding spaces in these compounds made of gyroids.
A final interesting application is in molecules called diblock copolymers. These molecules occur in many kinds of plastics, rubbers, and adhesives. In a diblock copolymer, two large molecular blocks, say A and B, appear. In some cases these molecules may be bonded together into long chains. In other cases the two blocks can separate into many regions that contain mostly A blocks and mostly B blocks. In the space where the two regions meet there is a kind of competition between the two types of blocks. Scientists have long observed gyroids and other triply periodic minimal surfaces as these separating spaces. Molecules may even have the ability to self-assemble into a gyroid, which could have future applications in nanostructures.
Mathematicians and scientists who study minimal surfaces have many tools at their disposal. Before computers were ubiquitous, one would often build a physical model out of soap, plastic, or paper to help visualise the surface. Now, of course, we often use computers to develop rotatable models. You can play with a rotatable gyroid here.
Further reading
You can read more about minimal surfaces on Plus:
- Kelvin's bubble burst again
- Double bubble is no trouble
- Swimming in mathematics
- Getting a handle on soap
About the author

Adam Weyhaupt received a B.A. in Mathematics and a B.S. in Mathematics and Computer Science from Eastern Illinois University in 2001 and the M.A. and Ph.D. in Mathematics from Indiana University in 2002 and 2006 respectively. He is interested in minimal surfaces and pretty much any problem that he can involve undergraduates with, including geodesics on polyhedra and problems at the intersection of maths and politics. In his (rumoured) spare time, he enjoys being outdoors with his spouse and two children.
Comments
Anonymous
It's possibly quiet irrelevant for this subject, but you mentioned it there. Why the honeycomb lattice is doubly periodic, not triply periodic? What is about vector rotated for -30 degrees? Thanks in advance.
Anonymous
Hi. It's only called doubly periodic because two directions are sufficient to cover the entire plane. You need atleast two directions to cover the entire plane ( they can be either +30 degrees and +90 degrees from the horizontal line or you can also choose -30 and +90 from the horizontal axis or you can choose any other two directons which can tile up the entire plane). The exact vectors used are not important but what is important is that you need "two" of them to cover the entire plane.
Xu
Fantastic article!
Just a small question: sometimes i read "double gyroid" in papers (e.g. the PNAS paper for Butterflies), but I think all gyroid cubic lattices are double so that when we talk about it we dont have to mention double. is that right?
Alistair
Hi Adam,
I was wondering if you knew the source/origin of the trigonometric equation:
You mentioned it is approximated by the sinxcosy+sinycosz+sinzcosx = 0.
Do you know how the trig equation was discovered or know how different the elliptical integral version is to the trig function?
Cheers
Alistair
Ralph Dratman
I too would very much like to know the answer to Alistair's question!
Thank you.
Ralph
HL
Hi, thanks for the excellent article! I recently made a presentation about TPMS topic which included gyroid. One question I received was "Why is it called a gyroid?" I have no answer for this and wonder whether you know? Thanks.
David
Q. Why is it called a gyroid?
A. https://en.wikipedia.org/wiki/Alan_Schoen#Contributions
Alan Schoen is best known for discovering (while working at NASA) a minimal surface that he named the gyroid. The name stems from the impression in the gyroid's structure that each continuous channel in the array, along different principal crystallographic axes, has connections to additional intersecting channels, which “gyrate” along the channel length.