In our recent Plus article Tasty maths, we introduced Zipf's law. Zipf's law arose out of an analysis of language by linguist George Kingsley Zipf, who theorised that given a large body of language (that is, a long book — or every word uttered by Plus employees during the day), the frequency of each word is close to inversely proportional to its rank in the frequency table. That is:

\ $ P_n \propto 1/n^a $

where a is close to 1. This is known as a "power law" and suggests that the most frequent word will occur approximately twice as often as the second most frequent word, which occurs twice as often as the fourth most frequent word, etc. A famous study of the Brown Corpus found that its words accorded to Zipf's law quite well, with "the" being the most frequently occurring word (accounting for nearly 7% of all word occurrences — 69,971 out of slightly over 1 million), and "of" the second most frequent (3.5% of all words).

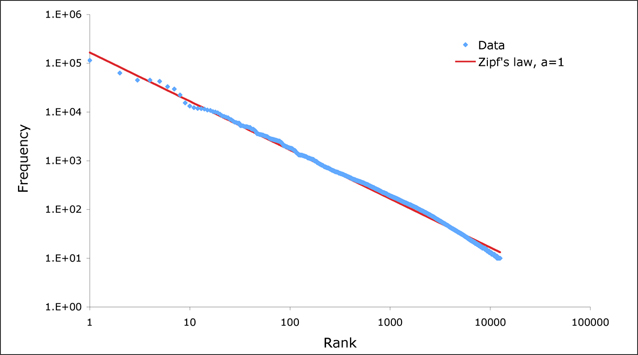
The frequency of words on Plus fit the Zipf distribution very well.

Never one to turn down a challenge, Plus set about checking if the frequency of words on all Plus pages matches the Zipf distribution, and as you can see in the chart, it fits remarkably well! The most popular word on Plus is "the". "The" is mentioned 114,001 times, or 6.86% of all words. Second in line is "of" occurring 62,964 times, and third is "to", occurring 4,5045 times. Unsurprisingly, the word "maths" features more highly than in normal usage, coming in at 40th place having been mentioned 4,829 times. "Mathematics" is at 51st and "mathematical" at 54th. "Plus" comes in at 76th, having been mentioned 2,454 times. A similar test has been done on word usage in wikipedia where it was found that Zipf's law holds true for the top 10000 words.

But what lies behind Zipf's law? There has never been a real explanation of why it should occur for languages and there is controversy surrounding whether it gives any meaningful insight into human language. Power laws relating rank to frequency have been demonstrated to occur naturally in many places — the size of cities, the number of hits on websites, the magnitude of earthquakes and the diameters of moon craters have all been shown to follow power laws. Wentian Li demonstrated in his paper Random Texts Exhibit Zipf's-Law-Like Word Frequency Distribution, published in IEEE Transactions on Information Theory, that words generated by randomly combining letters fit the Zipf distribution. In his randomly generated text, the frequency distribution of word length was exponential — that is, words of length 1 occurred more than words of length 2 and so forth, with frequency declining exponentially with word length. Li showed mathematically that the power law distribution of frequency against rank is a natural consequence of the word length distribution. His underlying theory is that the rank distribution arises naturally out of the fact that word length plays a part — long words tend not to be very common, whilst shorter words are. It is easy to see how this has occurred in the evolution of language. Li argues that as Zipf distributions arise in randomly-generated texts with no linguistic structure, the law may be a statistical artifact rather than a meaningful linguistic property.

In any case, word length in English does not follow an exponential distribution like a randomly generated text. Looking at Plus words, you can see that the most common word length is 3:

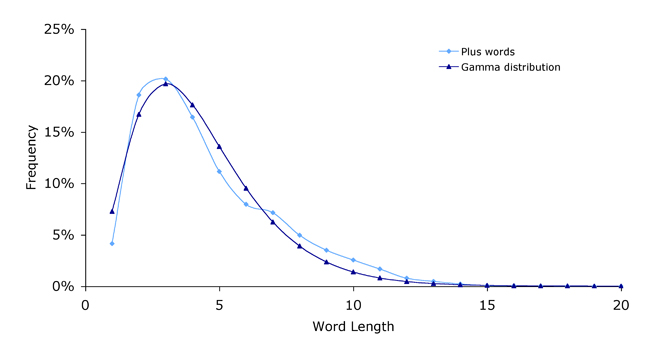
The length of words on Plus fit a gamma distribution very well.

The distribution nicely fits the curve: \ $$ f = a L^b c^L $$ where\ $ L $ is word length, $a = 0.16, b=2.33 $ and $ c=0.49. $ This is a form of the gamma distribution and the fact that it fits is similar to the findings of Sigurd, Eeg-Olofsson and van Weijer. Wi's method of relating the exponential distribution of the randomly generated text to rank — in which you knew that each word of length L occurs more frequently than each word of length L+1 and so has higher rank — does not work as the peak is for words of length 3 (not 1).

The jury remains out as to whether there is any significance in Zipf's law — does it cast light on the way we structure language and how language evolved? Or is it simply a statistical artifact? What do you think?

Further reading

MEJ Newman has put together a very nice article Power laws, Pareto distributions and Zipf’s law in Contemporary Physics.