Myths of maths: The four colour theorem

Following Brexit we are faced with the worry of the possible break-up of the United Kingdom. Suppose that Scotland and Wales become independent, but the Northern Island does not? How will this alter the map? Well, one of the things that will happen is that it will no longer be possible to colour the map of the British Isles with four colours.

If you know a bit of maths, then this may surprise you. There's a very famous result which states that every map can be coloured with at most four colours. However, the result depends upon what you mean by a map. This is not so much a myth, more of a misquotation.

Maps showing different countries have been produced since the 1800s. To distinguish between the countries it was useful to colour them in different colours. A simple rule for doing this was that any two countries which shared a border, other than meeting at a point, should have different colours. Now, it costs money to print a coloured map, so map makers aimed to find the smallest number of colours needed to colour the map with the "no touching condition". It was found experimentally that all of the maps considered only needed four colours to colour them in. Here is an example of a map of the world coloured with exactly four colours with no adjacent countries having the same colour.

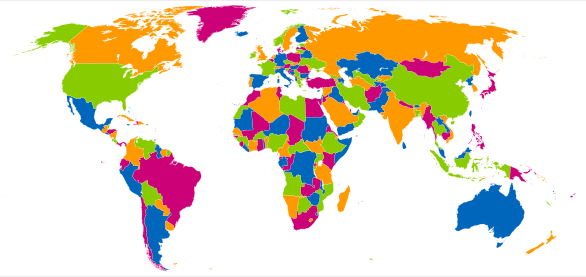
A map of the world in which the continents are coloured using four colours. If we take the oceans into account, however, we need five colours (see below for an explanation). Image Fibonacci, CC BY-SA 3.0.

This discovery led the mathematicians of the day to conjecture that every map on the plane needed at most four colours to colour it with the above rules. This conjecture was first proposed in 1852 by Francis Guthrie, who was trying to colour the map of counties of England. A first purported proof was given by Alfred Kempe in 1879. This proof was later shown to be incorrect, but was modified at the time to show that any planar map could be coloured with at most five colours. However the original problem, despite the attempts of many mathematicians, remained open. The four colour conjecture rapidly became one of the most celebrated problems in mathematics.

The four colour theorem was finally proved in 1976 by Kenneth Appel and Wolfgang Haken. The proof itself was remarkable and gained a great deal of notoriety because it was the first major theorem to be proved using a computer. (Essentially a mathematical analysis reduced the problem to a large, but finite, number of maps, each of which was then checked by a computer to see if it could be four coloured). Initially, this proof was not accepted by many mathematicians, because it was impossible to check by hand. However I think quite the opposite. I believe that this proof has ushered in a new way of doing mathematics. Indeed it has led the way to many other proofs by computer, including some of my own work. (See this article for more on computer proofs.)

The result is also important in modern WiFi technology. Imagine different WiFi transmitters, for example in an office block, all using different frequencies. To avoid interference we have a rule that no two adjacent WiFi transmitters should use the same frequency. The question we then ask is, "how many frequencies are needed to give a non-interfering network"?

It doesn't take much imagination to see that this problem is exactly the same as the four colour problem. So we only need four frequencies. Easy! Well, no, in fact we need more. Possibly many more. The problem arises, for example, in an office block, when different WiFi transmitters are assigned to different companies, and the company wants all of its transmitters to share the same frequency. This rapidly increases the number of frequencies that we need.

The same issue arises when we try to colour a map. By this I mean exactly what I say. A map. The sort of map that you would find in an Atlas. The issue arises in maps when countries have regions which are separated, or are possibly part of an Empire. These regions introduce an extra thing to consider when colouring the map, as they all have to have the same colour. The British Empire for example had all of its territories coloured red on the map. It also arises when the map has lakes, seas, or oceans. Not unreasonably all of these should be coloured blue. Below is an example of a map with two lakes. These I have coloured blue. The boundaries between the countries are indicated by black lines.

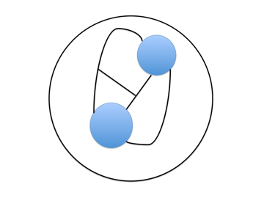
I challenge you to find a way to colour this map in four colours, whilst keeping the lakes blue. It can't be done — five colours are needed. The same applies to the map of the world above, if we take the oceans into account and realise that the colour white is also a colour, giving a total of five colours. The map can be coloured using four colours but only if some countries have the same colour as the sea. This makes them looks like lakes, and leads to a very confusing map indeed.

So, how does this affect the map of the British Isles? If there is independence of the home nations, then they will no doubt adopt their traditional colours of white for England, red for Wales, and dark blue for Scotland. The British Isles is surrounded by the light blue sea. Although Wales and Scotland do not touch they need different colours as the Welsh (and English) will need an embassy in Scotland which will need to be coloured the same colour as the nation. The question is: what is the colour of Ireland? If the home nations all have an embassy in Ireland with their own colour, then Ireland must have a different colour again (green of course). So we need five colours (at least).

So what is the myth? The four colour theorem as carefully stated (for non-contiguous planar graphs) is certainly true. But one thing it does not necessarily apply to is an actual map.

About the author

Chris Budd.

This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.