Back to the Do you know what's good for you package
Back to the Constructing our lives package
The Kelvin structure is made up of truncated octahedra. Image: Andrew Kepert.
A researcher from the University of Bath has tackled an old geometric problem with a new method, which may lead to advances in creating hip replacements and replacement bone tissue for bone cancer patients. The Kelvin problem, posed by Lord Kelvin in 1887, is to find an arrangement of cells, or bubbles, of equal volume, so that the total surface area of the walls between them is as small as possible — in other words, to find the most efficient soap bubble foam. The problem is relevant to bone replacement materials because bone tissue has a honeycomb-like structure, similar to a bubble foam.
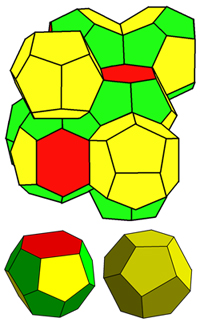
The Weaire-Phelan structure (top) is made up of tetrakaidecahedra (bottom left) and irregular dodecahedra (bottom right).
Kelvin suggested that the solution to his problem was a structure made up of slightly curved copies of a truncated octahedron: a shape with six square faces and eight hexagonal faces, which you get when you cut the corners off a three-dimensional diamond shape. Kelvin's structure, as his foam became known, was believed to be the most efficient solution for over 100 years, until the physicists Denis Weaire and Robert Phelan showed in 1993 that there is an even better foam. The Weaire-Phelan structure consists of two different bubble shapes: an irregular dodecahedron, which has twelve irregular pentagonal faces, and a solid with two hexagonal and twelve pentagonal faces, known succinctly as a tetrakaidecahedron. The structure is completely regular, and therefore easy to construct, but it also mimics the irregular appearance of a real foam rather well. This is why it was chosen as the inspiration for the 2008 Olympic swimming venue in Beijing, known as the Water Cube (see Plus article Swimming in mathematics to find out more).
The Water Cube, built for the 2008 Beijing Olympics, was inspired by the Weaire-Phelan structure. Image © Chris Bosse.
Phelan and Weaire showed that their structure's surface area is 0.3% less than that of Kelvin's solution. Although an infinite number of foams that beat Kelvin's structure have been found since 1993, the Weaire-Phelan structure remains the most efficient of them all. But whether or not there is an even more efficient foam out there, waiting to be discovered, still isn't known.
Gabrielli's new structure.
The new research comes from Ruggero Gabbrielli, who studied the honeycomb-like structure of bone replacement materials for his PhD in mechanical engineering at the University of Bath. Gabbrielli's new foam, a complex structure made up of polyhedra with 13 and 14 faces, doesn't beat the Weaire-Phelan structure in terms of packing efficiency, but the method he used to find it represents a new way of approaching the problem. Ultimately, it could discover more efficient foams than the ones currently known, and possibly even lead to a proof showing that a given structure is indeed the best possible.
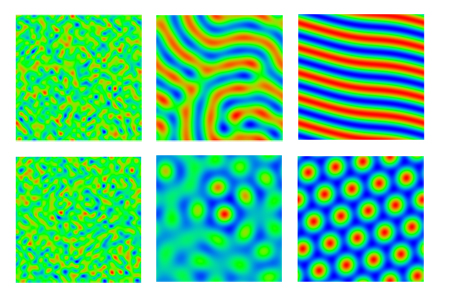
The Swift-Hohenberg equation in action. The top row shows the image on the left evolving into a stripy pattern. In the bottom row the parameters have been chosen to give a hexagonal pattern. Image: Michael Cross.
Gabbrielli's method uses the Swift-Hohenberg equation, a partial differential equation developed in 1977 to describe the transfer of heat through fluids. The equation can be used to generate patterns in two dimensions. Imagine a rectangular digital image, in which the location of each pixel is given by a pair
of co-ordinates 
, and the colour of the pixel at is defined by a numerical value 
. The Swift-Hohenberg equation gives a rule dictating how the colour values of the various pixels should change over time and space. The equation depends on two parameters, which you're free to choose. If you let your image evolve according to the equation's rule, then depending on the parameter values you chose, you'll soon see a regular pattern emerge on your screen. Some parameters will give you stripes while others give you spots - it's possible to evolve different patterns from the same image, simply by choosing different parameters. It doesn't matter what kind of image you choose to start with, as a given choice of parameters will always produce the same kind of
pattern. (See this website to see an animation of this process.)
Gabbrielli realised that the Swift-Hohenberg equation can also be used to generate patterns in three dimensions. With the help of the equation and other existing techniques, he developed a new way of "growing" a whole range of foams — not as real structures, but as models on a computer. Some of these foams are indeed new: one of them is the first to contain quadrilateral, pentagonal and hexagonal faces, and it does so in ratios that are very similar to those occurring in real foams. Most importantly, its surface area is less than that of the Kelvin structure, raising hopes that the method may in future find foams that even beat the Weaire-Phelan structure. Gabbrielli's results have been published in Philosophical Magazine Letters.