Outer space: Blowin' in the wind

How much of the wind's power can a windmill catch? Quaint old windmills, sleek wind turbines, or ugly great propellers in the countryside all look rather different, but what they aim to do is tap into the power of a great moving mass of air to rotate an axle and then generate an electrical current. It looks as if there must be a best-possible result because if the windmill had no effect on the incoming wind, so the speed of the passing wind stayed the same, then no power would be extracted. Then again, if the wind was brought to a complete halt by the windmill sails — if they formed a solid disk — then the sails wouldn't turn and there would be no power generation. So somewhere in between these two extremes there might be a most efficient windmill.

A windmill's sails sweep out an area $A$. The air approaches at a head-on speed $U$, and then leaves behind the sails at a lower speed $V$. This loss in wind speed as a result of the sails' action is what enables power to be extracted from the moving air by the windmill. The average speed of the air at the sails is just the average of the up and downstream speeds: $\frac{1}{2}(U + V)$. The mass per unit time of air passing through the rotating arms is therefore

                                                        $F = \rho A \times \frac{1}{2}(U+V),$

where $\rho$ is the density of air. The power generated by the windmill is just the difference in the rate of change of the kinetic energy of the air before and after passing the sails. This is \\ \\                     $P = \frac{1}{2}FU^2 - \frac{1}{2}FV^2.$ \\ \\ If we substitute the first formula for $F$ in this equation, then we see that the power generated is \\ \\                     $P = \frac{1}{4} \rho A (U^2 - V^2)(U+V).$

But if the windmill had not been there, the total power in the undisturbed wind would have just been

                    $P_0 = \frac{1}{2} \rho A U^3.$

So the efficiency of the windmill in extracting power from the moving mass of air is going to be $P/P_0$, which equals 1 when $P=P_0$, indicating 100\% efficiency as a power generator. Dividing the last two formulas we have $$P/P_0 = \frac{1}{2} (1-(V/U)^2) \times (1+V/U).$$

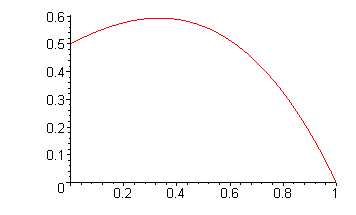
The graph of the efficiency function. The maximal efficiency occurs for V/U = 1/3.

This is an interesting formula. When $V/U$ is small, so there is a big drop in wind speed, $P/P_0$ is close to 1/2; when $V/U$ approaches its maximum value of 1, and there is little drop in wind speed, $P/P_0$ tends to zero. Somewhere in between, $P/P_0$ takes its maximum value, and you should check this happens when $V/U = 1/3$ (find out how). In that case, the power efficiency $P/P_0$ has its maximum value of 16/27, or about 59.26\%. This number was first calculated by the German engineer Albert Betz in 1919. It gives the maximum possible efficiency of a perfect windmill or rotor of any sort in extracting energy from moving air.

In practice, good wind turbines manage to achieve efficiencies of only about 33\% of the Betz maximum after taking into account the efficiency of their blade shapes, their electricity generation efficiency, and various losses in their cables and energy exchangers. The maximum power that can be extracted is $\frac{8}{27}P_0$. If the diameter of the rotor's circular path is $d = 2m$ then the area swept out is at most $A=\pi d^2/4$, the density of air is $\rho = 1.23 Kgm^{-3}$, and the windmill operates at one-third efficiency due to other power losses, then the actual power output is $$P \approx 0.38 \times (U/10ms^{-1})^3 \;\; kilowatts.$$ If the average wind speed was $10ms^{-1}$, then the power extracted is $P \approx 0.38$ kilowatts compared with the available wind power of $P_0 = 1.93$ kilowatts. However, the final step in our calculation using the average wind speed significantly underestimates the wind power that can be extracted in practice. Can you see why?