The patchwork multiverse

One man's abstract is another man's concrete. Nearly all ordinary folk, and even some physicists, would consider string theory to be a highly theoretical enterprise. But to Raphael Bousso, strings are intimately tied to understanding the universe we see around us. "The motivation is to understand how Nature works, and what's going on out there," he says.

Raphael Bousso.

Which is just as well, for Bousso is trying to solve one of the biggest puzzles in the cosmos: Just why is the universe so large? Bousso's quest has led him to consider a multitude of universes and, in particular, how the value of the cosmological constant — the intrinsic energy of the vacuum of space-time — could vary across different universe patches. The answer, Bousso claims, is "the first example of an experimental success of string theory."

It makes sense to look for a connection between the cosmological constant and the size of the Universe. Many physicists believe that vacuum energy is the mysterious dark energy that is causing the expansion of the Universe to accelerate. To fit with the cosmos that we see around us, the value of the constant should be small. The trouble is that this is in violent disagreement with calculations of vacuum energy from quantum field theory, by some 120 orders of magnitude (see here to find out more).

In 1997, Steven Weinberg, of the University of Texas, Austin, came up with the first realistic prediction for the value of the cosmological constant. Weinberg noted that there comes a time in the evolution of the universe when the cosmological constant—which repulses gravity and causes spacetime to expand faster and faster—becomes dominant. He realised that if the constant was much larger than 10^-120, it would dominate the universe too early, before galaxies, and in turn life, could be formed.

Underpinning the Universe

This allowed Weinberg to ask the question: What's the most likely value of the cosmological constant that would be seen by observers in our Universe? The answer: 10^-120. Weinberg's prediction was borne out by experiments to within a few orders of magnitude. "But the thing that was missing from the whole story was the theoretical underpinning," says Bousso.

As Weinberg himself noted, his arguments made sense only if there were many, many patches of spacetime, each with its own randomly-determined value of the cosmological constant. But in 1997, there wasn't a theory that could generate different patches of spacetime, each with a different vacuum.

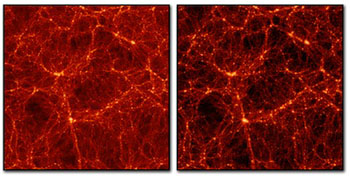
The distribution of galaxies in a Universe without dark energy (left) would differ from one in which dark energy is significant (right). Image: Lawrence Berkeley National Laboratory.

This is where string theory comes in. Over the past decade, Bousso along with Joe Polchinksi of the University of California, Santa Barbara, and others, has shown that string theory predicts the existence of more than 10⁵⁰⁰ vacua of spacetime. Essentially, each vacuum represents a different universe, each with different values for the cosmological constant and with different particles and forces.

The physical realisation of this ensemble is referred to as the multiverse. With this theoretical underpinning in place, Bousso and Polchinski asked the same question that Weinberg did: What would be the most likely value of the cosmological constant that would be seen by an observer? They were able to show that the landscape would have regions with a cosmological constant that tallied well with observations.

But soon it became clear that the analysis suffered from a profound problem: How do you calculate the number of observers in a seemingly infinite Universe?

Bousso's answer was to limit himself to thinking only about an imaginary observer who lives forever. Because of the finite speed of light, this observer can only see events within a certain region of their Universe—their causal patch. Bousso has calculated that the size of the causal patch doesn't change much over the lifetime of the long-lived observer. But inside this causal patch, the cosmological constant has a tremendous effect. As soon as it becomes dominant, it starts to accelerate the expansion of spacetime, and very soon dilutes the matter inside the causal patch.

"If the cosmological constant starts becoming important before the observers form, then there just won't be very many observers opening their eyes in the region where you are allowed to count them," says Bousso.

Time of life

Using the causal patch technique, Bousso found that the cosmological constant is related to the time at which observers inhabit any given universe. Plugging the age of our universe into his equations gave Bousso a universe that would be about 10^61.5 Planck lengths across and would have a cosmological constant of 10^-123 — both of which agree with observations. In fact, the value of the cosmological constant obtained in this manner is more precise than the one calculated by Weinberg.

But is there a fundamental constraint on when observers appear? Yes, says Bousso. And it has to do with the size of the landscape of string theory. It turns out that despite the extraordinarily large number of vacua in the string landscape, not all of them are cosmologically-viable, in the sense of giving rise to an expanding universe and hosting observers. And in most vacua in which the formation of observers is not hindered by the cosmological constant, observers form as late as possible in the evolution of the universe. In such a scenario, Bousso's calculations show that the smallest possible value of the cosmological constant is given by the inverse of the number of viable vacua.

So, the origin of these numbers—why the cosmological constant is not smaller and why the universe is not bigger—has to do with the finiteness of the string landscape, explains Bousso.

"It actually explains the cosmological constant in a way that previous theoretical attempts have utterly failed," he says.

About this article

This article is part of our Who's watching? The physics of observers project, run in collaboration with FQXi. It first appeared on the FQXi Communities website. Click here to see more articles and videos about questions to do with observers in physics.