From planets to universes (part I)
This article is based on a lecture given by Martin Rees at Stephen Hawking's 70th birthday symposium. It is published here by permission.

Martin Rees speaking at Stephen Hawking's birthday symposium.
It's a privilege to have this platform to congratulate Stephen Hawking. His insights will live on in the annals of science. He's enlightened millions through his books and lectures — and inspired still more by his personal example. We first met as graduate students. Astronomers are used to large numbers, but few are as large as the odds I'd then have given against this celebration today.
Back then, Stephen and I shared two bits of good luck. First we were both in the research group at the Department of Applied Mathematics and Theoretical Physics in Cambridge led by Dennis Sciama — a charismatic and enthusiastic man. Stephen was two years ahead of me. George Ellis had just finished his PhD, and Brandon Carter was an exact contemporary.
We all had a second piece of good luck: the mid-1960s saw the birth of relativistic astrophysics. Astronomers discovered the first compelling evidence that our Universe had expanded from the Big Bang. And they had discovered objects like neutron stars and quasars, where Einstein's theory was crucial, not just a tiny correction to Newton's. There were also mathematical insights, especially from Roger Penrose whose work with Stephen and with George Ellis deepened our understanding of black holes and the Big Bang.
The research community was then quite small — indeed most relativists were associated with one of three "schools": Dennis Sciama's, and those centred on John Wheeler in Princeton and Yakov Zeldovich in Moscow.
That's enough history. The good news is that today is an equally good time for young researchers — the pace of advance has crescendoed rather than slackened. We've discovered a whole menagerie of exotic objects, and surveyed millions of galaxies. The age of the Universe, and its ingredients, are pinned down to a precision of a few percent, its temperature is measured more precisely still.
But the advances bring into focus some deeper mysteries — the main questions that challenge us today couldn't even have been formulated back in the 1960s.
We study the Universe on four levels. First, we must explore what's out there. Astronomy is the grandest environmental science. We want to interpret the phenomena — realising that they manifest conditions far more extreme than can be simulated in the lab. We want, moreover, to understand not just the way things are now, but how the cosmic panorama, of which we're part, emerged from our Universe's hot dense beginning. And what its long-term future is too.
Hunting for distant planets
Stephen Hawking was asked on the BBC Today Programme what new discovery would excite him most. He said it would be finding intelligent life in space. I agree with him — I'm not holding my breath. But this gives a pretext to mention the hottest current topic in astronomy, even though it's not something Stephen has himself worked on.
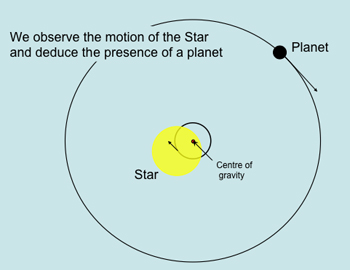
Figure 1: Image courtesy NASA.
This is the realisation that many other stars — perhaps even most of them — are orbited by retinues of planets, like the Sun is. These planets are not detected directly but inferred. The prime technique is shown in figure 1. If a star is orbited by a planet, then both planet and star move around their centre of mass — the barycentre. The star, being more massive, moves slower. But the tiny periodic changes in the star's Doppler effect can be detected by very precise spectroscopy [see Hunting for life in alien worlds]. Already more than 500 extra-solar planets planets outside our solar system have been inferred in this way.
The evidence pertains mainly to giant planets — objects the size of Jupiter or Saturn. Detecting Earth-like planets — hundreds of times less massive — is a real challenge. They induce motions of merely centimetres per second in their parent star.
But there's another technique that works better for these smaller planets: looking for their shadow. A star dims slightly when a planet is in transit in front of it. An Earth-like planet transiting a Sun-like star causes a fractional dimming, recurring once per orbit, of one part in 10,000. The Kepler spacecraft has been monitoring the brightness of over 100,000 stars, at least twice every hour, with this precision. It's already found more than 2,000 planets, many no bigger than the Earth.
We're specially interested in possible "twins" of our Earth — planets the same size, on orbits with temperatures such that water neither boils or stays frozen. And the real goal, of course, is to see them directly. But this is hard. To realise how hard, suppose an alien astronomer with a powerful telescope was viewing the Earth from 30 light years away — the distance of a nearby star. Our planet would seem, in Carl Sagan's phrase, a "pale blue dot", very close to a star (our Sun) that outshines it by many billions: a firefly next to a search light. The shade of blue would be slightly different, depending on whether the Pacific ocean or the Eurasian landmass was facing the alien astronomer. They could infer the length of our day, the seasons, the gross topography, and the climate. By analysing the faint light, they could infer that the Earth has a biosphere.
Within 20 years, a huge telescope planned to be built by the European Southern Observatory — with a mirror 39 metres across — will be drawing inferences like this about planets the size of the Earth, orbiting other Sun-like stars.
Would there be any life on them — even intelligent life? Perhaps life so intelligent that it would find string theory a doddle? Here we're still in the realm of science fiction. (But it's better to read first-rate science fiction than second-rate science, which is far less stimulating and may also be wrong.)
Star births and deaths
What has surprised people about these planetary systems is their great variety. But their existence wasn't surprising because of what we've learnt about how stars form and how they die. They form in places like the Eagle Nebula via the contraction of clouds of dusty gas.
If the cloud has any angular momentum, it will spin faster as it contracts and spin off a dusty disc around the so-called protostar, as shown in figure 3. In such a disc dust agglomerates into rocks and planets — this should be a generic process in all protostars.

Figure 3: Artist's conception of the dust and gas disk surrounding the star Beta Pictoris. A giant planet may have already formed and terrestrial planets may be forming. The inset panels show two possible outcomes for mature terrestrial planets around Beta Pic. The top one is a water-rich planet similar to the Earth; the bottom one is a carbon-rich planet, with a smoggy, methane-rich atmosphere similar to that of Titan, a moon of Saturn. Image: NASA/FUSE/Lynette Cook
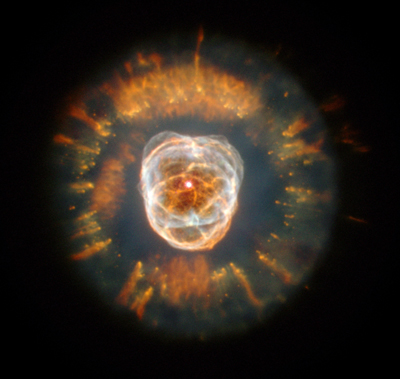
We do not only see stars forming, but we see them dying. The image below shows the Eskimo Nebula, whose gas composed the outer layers of a sun-like star only 10,000 years ago. This is how our Sun will look like in 6 billion years.
Our galaxy is a huge ecological system where gas is being recycled through successive generation of stars. And it will continue for billions of years. So let me expand a little on our future.
The future
The stupendous time spans of the evolutionary past — the four billion years of Darwinian evolution — are now part of common culture (though maybe not in Kentucky and parts of the Muslim world). But most people somehow still think that we humans are the culmination of the evolutionary tree. That hardly seems credible to an astronomer. The Sun's got 6 billion more years before its fuel runs out. It then flares up, engulfing the inner planets.
Any creatures witnessing the Sun's demise won't be human. They'll be as different from us as we are from a bug. Posthuman evolution — here on Earth and far beyond — could be as prolonged as the Darwinian evolution that has led to us — and even more wonderful.
Moreover, the death of the Sun won't be the end of the Universe. Indeed, our Universe may expand forever, becoming ever darker, ever emptier. To quote Woody Allen, eternity is very long, especially towards the end.
Distant galaxies
Let's now enlarge our spatial horizons to the extragalactic realm. If you could get two million light years away from Earth and look back at our galaxy, it would look like this.

Figure 5: The Andromeda Galaxy. Image courtesy NASA.
That is of course Andromeda — the nearest big galaxy to us. A spinning disc, viewed obliquely, with a hundred billion stars spinning around a central hub.
Figure 6 shows the Whirlpool Galaxy, estimated to be 23 million light years away from our galaxy, seen face on.
We have huge samples of galaxies like these to study. But how much can we actually understand? Physicists who study particles can probe them and crash them together in accelerators. Astronomers can't crash real galaxies together. And galaxies change so slowly that we only see a snapshot of each. But we can do experiments in a "virtual Universe".
Here is a virtual collision — 1015 faster that it would actually happen. Everything in each galaxy exerts a gravitational pull on the other — causing distortion, tidal plumes and so forth. This could happen to our galaxy and Andromeda in 4 billion years.
Simulation by Joshua Barnes (IfA, University of Hawaii) and John Hibbard (National Radio Astronomy Observatory).
When we look in the real sky we find very similar looking systems like the one shown in figure 7.

Figure 7. Image courtesy NASA Marshall Space Flight Center.
Having done such simulations, we'd infer that these two galaxies have got dangerously close — they're in the process of merging.
We can do such simulations making different assumptions about the mass of stars and gas in each galaxy, and so forth and see which matches the data best. Importantly, we find, by this method and others, that all galaxies are held together by the gravity not just of what we see.
They are also bound together by a mysterious substance known as dark matter [see What is dark matter? to find out more.] That's an inference that has been firmed up since the 1980s.
But more recently we've had a big surprise. On the cosmic scale gravitational attraction is overwhelmed by a mysterious new force latent in empty space which pushes clusters away from each other. The cosmic expansion is speeding up. The number that describes this cosmic repulsion is called Lambda [you can find out more in Lambda marks the spot], and we will return to Lambda later on in this lecture.
This is the end of the first part of this article. You can read the second part here.
About the author

Martin Rees is Astronomer Royal and Professor of Cosmology and Astrophysics at the University of Cambridge.