Protecting the nation
Back to the What's the best medicine package
Back to the Do you know what's good for you package
The health scare surrounding the MMR vaccine may lead to epidemics.
Vaccination is an emotive business. The furore around the MMR vaccine and autism has shown that vaccination health scares can cause considerable damage: localised epidemics of measles have already occurred because parents decided not to have their children vaccinated when the MMR scare was acute, and there are fears that a more widespread epidemic will follow. In the 1970s concerns over the safety of a whooping cough vaccine led to several serious epidemics that resulted not just in illness, but also in children's deaths.
The fears surrounding vaccines are often unfounded — in the case of MMR and autism they definitely were — but they are also understandable. After all, you are talking about injecting perfectly healthy people with antigens to a potentially dangerous disease, and if a vaccine has been produced quickly there are fears that it may not have been sufficiently tested. So what kind of effort goes into setting up a vaccination programme and making sure a vaccine is safe?
Who should be vaccinated?
The H1N1 vaccination programme that has just been launched in the UK prioritises groups of people that are most at risk from an infection, for example those with heart conditions, pregnant women, or those in regular contact with patients of other conditions like cancer. "It's unlikely that we'll be able to stem the rate of infection at this stage," says Paddy Farrington, Professor of Statistics at the Open University, who specialises in epidemiology and vaccination. "In a sense, that battle has been lost. What is important now is to mitigate its impact. It's the consequences of the infection that matter now: there are certain groups that are more at risk of developing serious disease [as a result of an infection] than others, and these need to be protected." So in this case it's a question of disease control, rather than infection control.
By contrast, most other vaccination programmes, for example the MMR vaccine, which protects against mumps, measles and rubella, or a HIV vaccine once it becomes available, aim to control or even eradicate a disease. These kind of programmes are planned years in advance. Decisions like whether to implement a blanket vaccination programme for the whole public, or just target specific groups, are important not just for financial and practical reasons. "What you're effectively doing [when vaccinating] is intervening in the ecology of an infection, and that can have all kinds of consequences, negative as well as positive," says Farrington.
For example, before the MMR vaccine was introduced, there was a separate vaccination scheme for rubella, which was targeted at adolescent girls aged 12 to 14. The aim was to protect the babies they would go on to have from congenital rubella syndrome. Replacing this targeted and limited programme by a mass vaccination programme for young children increases the average age at infection, so there is a possibility that a higher proportion of infections will happen in pregnant women, even though the overall infection rate is reduced. This can be avoided if sufficient numbers are vaccinated. So before switching to MMR, the authorities needed to be sure that the programme would achieve a high enough coverage. "It's a question of logistics and of the acceptability of the programme," says Farrington. "For some years, what was done was to vaccinate children with MMR at 15 months, but keep the rubella programme for adolescent girls going until it was clear that it was no longer needed."
Model infections
Decisions on how to implement a vaccination strategy are usually made on the basis of mathematical models, which simulate how an infection spreads and how it will react to vaccination. Whether it's the large variety of human diseases, or animal infections like foot and mouth, these models tend to take the same format. A hypothetical population is divided into several classes, for example susceptible (S), infected (I) and recovered (R). The model assumes that each day (or whatever the time step you're using) individuals pass from one class to the next according to a mathematical rule.
For example, if b is the average number of contacts a person has a day and S is the proportion of the population that is susceptible to the disease, then you can assume that an infected person meets bS susceptible people a day on average. Assuming that the disease is passed on to all of them, bSI people pass from the susceptible to the infected class every day, where I is the current number of infected people. If people don't die of the disease, and the average number of days a person is sick is d, then the chance of recovery on a given day is 1/d, so you can assume that out of I infected people I/d pass over into the recovered class every day. This gives a simple model describing the evolution of the disease from a given starting position, and based on a number of assumptions.
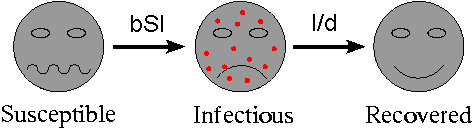
Transition rates between the three classes.
This model can be made more mathematical by phrasing the rules for transition from one class to the next in the language of differential equations. It can also be made more sophisticated by including assumptions on the birth and death rates in a population, and by including additional classes to reflect the heterogeneity of a real population. For example, the three classes mentioned above can be subdivided according to age group or gender, or you can add classes for those who are incubating the disease, but aren't yet contagious, and so on. (See the Plus article The mathematics of diseases for more about disease modelling.)
What makes these one-format-fits-all models appropriate for a particular disease is not just the scope for tailored compartmentalisation, but also the parameters which describe the transition rates between the different classes. It's these parameters that make it possible to simulate the impact of a vaccination strategy because vaccination works by moving vaccinated people out of the susceptible class. An important number in this context is the basic reproduction ratio, R, which measures the average number of people an infectious person will infect assuming that everyone in the population is susceptible. For swine flu, the basic reproduction ratio is probably somewhere around 1.5, compared to around 12 for measles. Together with the serial interval of the infection — the time that passes between acquiring the infection and passing it on — the basic reproduction ratio determines the overall rate of growth of an infection in the absence of vaccination.
"The purpose of vaccination policies is to bring the basic reproduction ratio down to an effective reproduction ratio which is less than one," says Farrington. "If you manage to vaccinate a sufficient proportion of the population to [achieve this], then each new infection will produce less than one other infection on average, so an imported infection may spread a little, but any such outbreak will eventually peter out." Assuming that everyone in the population makes contact with other people at the same rate, simple mathematics shows that the proportion of the population you need to vaccinate is just over 1-1/R, where R is the basic reproduction ratio. For example, if R=4 and you vaccinate more than 3/4 of the population, then this means that at least 3 out of the four people a sick person would infect on average are now protected, so the effective reproduction rate is now less than one.
The H1N1 virus. Swine flu has a basic reproduction ratio of around 1.5.
But in reality things aren't that simple, as people's contact patterns vary widely, in particular with age group. "You need to be able to represent the variation in contact patterns between various age groups [in a model]," says Farrington, "but that's not easy to do, because we don't have direct information on this." Scientists typically use data obtained from blood samples to find out if an individual has been infected with a disease in the past, and to deduce from that the rate at which the disease spreads in their particular age group. But this only tells you if an individual was infected, not who infected them. With some infections, for example those that are transmitted sexually, there is a realistic chance to describe the contact patterns by asking people about their sexual history, but this is controversial: in the 1980s the government of Margaret Thatcher blocked funding for just such a study, on the grounds that it was unduly intrusive.
"There remains a fundamental indeterminacy in [modelling contact patterns]," says Farrington. "It's necessary to try out various assumptions about who makes contact with whom, all of which are consistent with observations, but can have different implications. How to determine the contact structures remains an important issue in research into the mathematical and statistical analysis of infectious diseases."
Is it safe?
Like all medical drugs, vaccines are tested extensively for efficacy and safety before being licenced. New drugs are tested in humans using large-scale controlled trials, in which a group of volunteers who have been given the drug are compared to a control group of people who might have been given no treatment at all, a placebo, or an existing drug which represents current best treatment for whatever condition the drug is for. These trials can identify if the drug is effective, and if there are serious side effects. The problem with vaccines is that they are typically designed to be given to perfectly healthy people, often children, for preventive purposes, so it would be unethical to test them on very large groups. "Testing for very rare possible side effects, which might occur at the rate of one in 100,000, can only be done once the vaccine is out there being used, otherwise we'd just never have any vaccines," says Farrington. "So what's important is to have a sensitive system to detect possible rare problems with new vaccines when they are introduced and to monitor the performance of vaccines when they are being used."
Once the vaccine is used in the population, the only data you can realistically get hold of is routine information from hospitals and doctors on cases of particular conditions that you suspect may be adverse effects linked to a vaccine. You can look at how many of the people who became "cases" of a particular condition have also been vaccinated, and compare that to the number of unvaccinated cases. But in the absence of a randomised control group, it's hard to spot any bias that might have crept in: for example, an adverse effect that seems to occur more often in vaccinated people may not be due to vaccination, but to another factor, for example a pre-existing health condition which made it more likely that people were vaccinated in the first place.

Very rare side effects may only be detected once a vaccine is out in the population
Farrington became involved with this problem in the 1990s, when there were worries that a component of the MMR vaccine might cause a condition called aseptic meningitis. "Children recover from [aseptic meningitis] very quickly, but you don't want children to have any negative effects at all if possible, and even mild side effects can have a detrimental effect on the vaccination programme." He developed a method, called the self-controlled case series method, which uses a minimal amount of data about cases of a particular condition, and can therefore flag up potential problems quickly. Rather than looking at how many cases occur within the vaccinated and unvaccinated groups respectively, the method looks at when cases occur. While traditional methods for controlled trials would try and estimate the probability that an adverse effect occurs, Farrington's method is based on the conditional probability that the effect occurred when it did, given that it did occur. The result is a consistent estimate of the rate at which cases occur in the risk period right after vaccination, compared to the rate at which cases occur outside that risk period. If this estimate, based on routine information about cases from hospitals or GPs, rises above a certain treshold, then this is evidence that the cases are indeed a result of the vaccine.
Because it looks at variations over time, rather than between individuals, this method automatically controls for types of bias that are fixed over time: for example, if people become cases because of a pre-existing condition, rather than because of vaccination, then it's unlikely that they all become cases right after they've been given the vaccine, so the method is unlikely to be confounded by this bias.
In the case of the MMR vaccine, the self-controlled case series method proved successful. A particular component of the MMR vaccine was identified as a culprit behind cases of aseptic meningitis and replaced. The method was also used to investigate a possible link with autism, which was not confirmed. So while uncertainty surrounding vaccines can never be completely eradicated, Farrington's work and that of many other statisticians ensures that it's kept to an acceptable minimum.
It is ironic that the MMR vaccine is better known for a supposed adverse effect it definitely didn't have — autism — than for its success, or the fact that a real adverse effect — aseptic meningitis — was quickly spotted and the vaccine made safer. This is in part down to sensationalist media coverage, but also to understandable anxiety about anything to do with people's health. "Ever since the BSE problem and the autism and MMR crisis, there is a lot of questioning of vaccination policy in the British public, as evidenced by the MMR and autism issue," says Farrington. "It's important to have good surveillance systems and robust statistical methods to be able to find problems quickly or to be able to accumulate evidence that a vaccine is safe." Perhaps part of the problem is that the public are rarely made aware of the fact that, while there will always be some uncertainty, sophisticated statistical methods can go a long way at keeping it to a minimum. "You can never say with 100% certainty that a vaccine, or anything else for that matter, is safe, but you can accumulate evidence of safety. It's important to do that to dispel these fears, which are sometimes quite irrational and usually unfounded."
Back to the Mathematics of infectious disease package or the What's the best medicine package
About this article

Paddy Farrington studied pure maths and got a PhD in set theory from Leeds University, then spent many years doing other things — living in Hanoi in Vietnam, working as circulation manager for Marxism Today, and as Transport Officer in London — before deciding to take up statistics and doing an evening class at Birkbeck. He worked for 11 years as a statistician at what is now the HPA Centre for Infections, where he developed an interest in infectious diseases and vaccination. He joined the Open University in 1999 and currently works on statistical methods in vaccine safety, estimating transmission parameters for infectious diseases, and statistical methods for detecting outbreaks.
Paddy Farrington was interviewed by Marianne Freiberger, Co-Editor of Plus, in October 2009.