
Satanic science
As I turn on the heating on this miserable February day in North London I am very grateful for a basic fact of nature: that heat flows from hot to cold. If it didn't, then my radiator would have no chance of heating up my chilly room. If heat flowed from cold to hot, then the radiator would suck the little heat there is in the air out of it. Brrr.

James Clerk Maxwell (1831-1879).
So fundamental is this fact of nature that it has been elevated to a law of nature. One of the first people to state it clearly was the German scientist Rudolf Clausius in 1850. "Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time," he wrote. If you want to make heat flow against its preferred direction, as happens in a refrigerator, you need to put in energy (that's the "other change"), otherwise it just won't do it.
Today Clausius' law is known as the second law of thermodynamics (the first one being that energy cannot be created or destroyed). Thanks to Clausius, Lord Kelvin and James Clerk Maxwell (among others) we also know what heat actually is. It is a form of energy that comes from the molecules and atoms that make up a material. These vibrate, rotate or, in a liquid or gas, move around randomly, bouncing off each other as they go. The more vigorously they do this, the higher their average kinetic energy, and the hotter the material they're part of. You can see this whenever something melts. In an ice cube, for example, individual molecules are locked into a rigid lattice, but once you heat it up they start jiggling around and eventually break their chains, making the water warmer and also liquid.
This new understanding of the nature of heat was deep and apparently true, but it posed a problem. In 1867 Maxwell wrote to a friend about a thought experiment which suggested that the second law of thermodynamics could be broken. Heat could be made to flow from cold to hot without any effort invested. This scandalous process would be fuelled by information only; you could heat a room in that way, so you'd effectively turn information into energy.
Demonic heat
This thought experiment came to be known as Maxwell's demon and mystified scientists for more than a hundred years. Seth Lloyd, of the Massachusetts Institute of Technology in Boston (and so presumably also grateful for central heating), is an expert on Maxwell's demon and played a major role in its resolution.
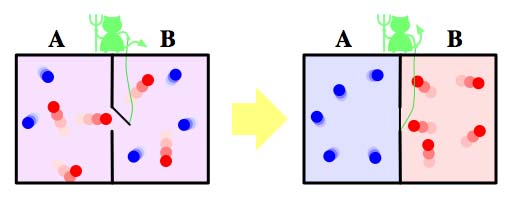
Maxwell's demon. Image: Htkym.
"Maxwell imagined a gas in a container," he explains. "Initially the gas is at equilibrium so everything is the same temperature. There is a partition at the centre of the container with a tiny little door in it. Manning the door is a 'demon', sufficiently small, agile and light-fingered to be able to detect the motion of individual molecules in the gas as they head towards the door. The demon sorts the molecules into hot and cold. If it sees fast molecules coming from the left, or slow molecules coming from the right, it will open the door, letting the fast molecules go from left to right and the slow ones from right to left. Whereas if it sees the opposite, then it keeps the door closed."
By this process the demon will gradually increase the average velocity of the molecules in the right side of the container and decrease it on the left. The right hand side of the box will heat up while the left cools down: heat will flow from the cold part to the hot part. You can set things up so that, overall, no energy needs to be invested to make that reverse flow happen. For example, if the door is on a spring, then the demon needs to invest a little energy to push it open, but that energy is repaid when the door swings shut again. The bottom line is that heat flows from cold to hot without any effort being put in to make that happen — the second law of thermodynamics is violated. All the demon needs to violate it is knowledge, information, about the molecules' motion.
Minimum wage
Esoteric as it may seem, Maxwell's demon had its roots in considerations that couldn't be more practical. The beginning of the nineteenth century saw the rise of the steam engine, but also pressed home an inconvenient fact: those engines were horribly inefficient. This inspired a young French engineer, Sadi Carnot, to work out theoretical limits on the efficiency of heat engines. These function by converting into work the heat that flows from a hot to a cold reservoir. In 1824 Carnot published a book, beautifully titled Reflections on the motive power of fire, in which he showed that the maximal efficiency any heat engine can hope to achieve depends only on the ratio between the temperatures Tcold and Thot of the two reservoirs. It's $$\mbox{Eff} = 1 - T_{cold}/T_{hot}.$$ This means that 100\% efficiency ($\mbox{Eff} = 1$) only happens if $T_{cold} = 0$. And since Carnot measured these temperatures in Kelvin, it means that 100\% efficiency could only happen if the cold reservoir was at absolute zero. That's -273.15 degrees Celsius, a temperature that is impossible to achieve. Therefore, any heat engine, no matter how perfect, is less than 100\% efficient. Some of the heat that is being transferred in the engine will always go to waste. Work comes at a price.
Some forty years after Carnot, Clausius put his mind to getting to grips with this inherent inability to do work that is present in any engine. He found a mathematical expression to quantify the amount of energy in a physical system that is unavailable to do work. That quantity, he wrote, might be called the "transformational content" of the system. But since he preferred names derived from the Greek he called it entropy, inspired by the Greek word "tropi" meaning "transformation", and chosen to be as similar as possible to the word "energy".
Classical definition of entropy
For a reversible process that involves a heat transfer of size $Q$ at a temperature $T$ the change in entropy $\Delta S$ is measured by $$\Delta S = Q/T.$$A reversible process is one in which no energy is dissipated (through friction etc). To see how this formula can be applied to more realistic irreversible processes and for an example calculation see here.
When applied to heat flowing from a hot body to a cold one, Clausius' definition shows that the entropy of the hot body decreases while the entropy of the cold one increases. However, the increase in the cold body is greater than the decrease in the hot one, so when taking the two bodies together, the overall entropy increases.
More generally, if you accept that heat naturally only flows from hot bodies to cold ones, and not the other way around, you can show that the entropy of a closed physical system (one that doesn't interact with its environment) can only increase or remain constant, it can't decrease. Conversely, if you are happy to believe that the entropy of a closed system can never decrease, then you can deduce that heat only flows spontaneously from hot bodies to cold ones. The two statements are equivalent, which is why the second law of thermodynamics is often stated in terms of entropy, rather than heat flow:
The entropy of a closed physical system never decreases.
Entropy is disorder
Carnot had come up with his result about heat engines even though he had a completely wrong idea of what heat was. He thought of it as a fluid, rather than the kinetic energy of molecules and atoms. Unfortunately he never had time to put right this mistaken belief. Six years after publishing his seminal work, Carnot died of cholera, aged only 36.

A Christmas pyramid: the fan blade at the top is powered from the heat of the candles.
It was the molecular interpretation of entropy, however, that eventually exorcised Maxwell's demon. Maxwell, Ludwig Boltzmann and others realised that entropy can be regarded as a measure of disorder in a system. To get an idea of how this might work, imagine a room with a burning candle in it. The heat of the candle can be converted into work. For example, you could use the hot air rising from it to power one of those German Christmas toys that have a fan blade at the top. Now imagine the same room after the candle has burnt out and the temperature is uniform throughout. You can't get any work out of this situation, so if you think of entropy as measuring the inability to do work, then it's clear that the room has a higher entropy when the candle has burnt out than when it is still burning.
But at the molecular level that second situation, with the candle burnt out, is also much less orderly. The fact that the air has a uniform temperature throughout means that fast and slow moving molecules are thoroughly mixed up: if they were separated out in some way, then you'd have a temperature gradient in the room. In fact, the thermal equilibrium the room finds itself in is also the state of maximal disorder. When the candle is still burning, by contrast, fast molecules are concentrated around the flame, making for a much more orderly situation.
But how do you rigorously quantify the amount of order or disorder in a system? A good analogy here is a pack of cards. When you buy it from the shop it comes arranged by suit and numerical value. There's only one way of doing this: that's perfect order. If you arrange the cards by suit only, there is more ambiguity as cards of the same suit could be arranged in any which way. That's a less orderly situation. If you want disorder, you shuffle the cards. The shuffling could leave your cards in one of a huge number of arrangements, each of which qualifies as disordered. So, you can quantify the amount of disorder in a system by counting the number of configurations the system's constituent components can be in without changing the system's overall nature.
Microscopic definition of entropy
Suppose that a gas in a particular macrostate, for example, it has a particular temperature or pressure. Write $W$ for the number of configurations its individual molecules can be in to preserve that macrostate. Then the entropy $S$ is $$S = k\ln{W},$$ where $k$ is Boltzmann's constant $$k = 1.38062 \times 10^{-23} J/K.$$ Here $J$ is Joule, the unit for energy, and $K$ is temperature in Kelvin. The formula is engraved in Boltzmann's tomb stone in Vienna. It works when all the configurations of molecules are equally probable to occur. There is a generalisation of this formula which works when they are not all equally probable. It's $$S = -k \sum_i p_i\ln{p_i},$$ where the $p_i$ is the probability of configuration $i$."Maxwell and Boltzmann figured out a formula for entropy in terms of the probability that molecules in a gas were in particular places and had particular velocities," explains Lloyd. That probability tells you how many different configurations those molecules can possibly have while the gas remains in the same state, so it quantifies the amount of disorder. According to this definition a hot gas has a higher entropy than a cold one. In a hot gas the average kinetic energy of the molecules is higher, so the kinetic energy of individual molecules can be spread over a wider range. And as we already hinted above, a gas in thermal equilibrium is also in a state of maximal entropy. (To understand why a higher average energy implies a wider spread, imagine two cars on a race track. If their average speed is 200 km/h, then the speed of an individual car is anywhere between 0 and 400 km/h. If the average speed is only 100 km/h, then the individual speeds are limited to lie between 0 and 200km/h.)
Entropy is information
It turns out that the definition of entropy in terms of disorder is equivalent to Clausius' original definition in terms of temperature and energy. And the disorder definition also provides a direct link to information. If a system is in a highly disordered state, then you need a lot of information to describe it: there are many configurations in which its constituent components might be arranged. If there is more order in the system, for example if all the molecules that make up a gas are moving in the same direction with the same speed, then you need much less information to describe it. The more disorder there is, the higher the entropy and the more information you need to describe the system.
"When the 20th century rolled around it became clear that entropy was proportional to the amount of information required to describe those molecules; their positions and velocities," explains Lloyd. "Entropy is proportional to the number of bits required to describe the motion of the atoms and molecules. Or, to put it differently, to the amount of information they themselves effectively contain."
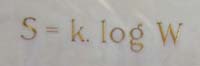
Boltzmann's entropy formula engraved on his tomb stone in Vienna. Image: Daderot
But what do these various interpretations of entropy mean for Maxwell's demon? The demon violates our first formulation of the second law of thermodynamics because it makes heat go from cold to hot without investing any energy. The heat accumulating in the left part of the box could then be converted into work, so if you interpret entropy as a measure of the system's inability to do work, then the demon violates the second formulation of the second law too, by decreasing that inability. And since the demon imposes some structure on a gas that was previously in equilibrium, it also violates the second law if you interpret entropy as a measure of disorder. Thus, the demon is guilty on all three counts, as you would expect seeing that the three interpretations are equivalent.
Next: How to exorcise the demon.
About this article
This article is part of our Information about information project, run in collaboration with FQXi. It addresses the question 'can information be turned into energy?'. Click here to see other articles from the project.
Seth Lloyd is professor of quantum mechanical engineering at MIT and external professor at the Santa Fe Institute. He is the author of over 150 scientific papers and of a popular book Programming the Universe. Marianne Freiberger, Editor of Plus, interviewed him in January 2014.
This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
Anonymous
Great article which explained a lot to me. Couple of typos ..
1. "If the average speed is only 100 km/h, then the individual speeds are limited to lie between 0 and 100km/h" - should this not read "0 and 200km/h"
2. There is a incorrect JCM caption on a photo on the second page.
Marianne
Thanks for pointing out those errors, we've fixed them!
Anonymous
It is not necessary that if average speed is 200 kmph then the speed of the car must lie between 0 and 400 kmph. It can cross 400 kmph but Average may still remain 200 kmph.
Anonymous
That's not correct, he talks about the average speed of 2 cars.
Themis Chronis
I need to point something very important in this otherwise very well written article. The author keeps mentioning that heat is the kinetic energy of the jiggling molecules. This is not true by any stretch. This is the Boltzmann energy aka internal energy and NOT heat. Gases, liquids and solids do NOT have heat. They have internal energy. The transferring of momentum and kinetic energy via the intra-molecular collisions is heat