Saving whales using Pythagoras

Submitted by Marianne on March 13, 2019

A beluga whale. Photo: Premier.gov.ru, CC BY-SA 4.0.

Whales are under threat from all sides: whaling, the degradation of habitats, toxins in the water, the damaging effects of sonar, and climate change.

There is also the very real danger of being struck by ships. To avoid whales, shipping crews need to know where they are. This is where Pythagoras' ancient theorem about right-angled triangles comes in: a simple application of the theorem can save whales!

Pythagoras' theorem

Pythagoras' theorem says that, given a right-angled triangle labelled as below, the area $c^2$ of the square on the hypothenuse is equal to the sum $a^2+b^2$ of the areas of the squares on the other two sides. (See the below for a statement in limerick form.)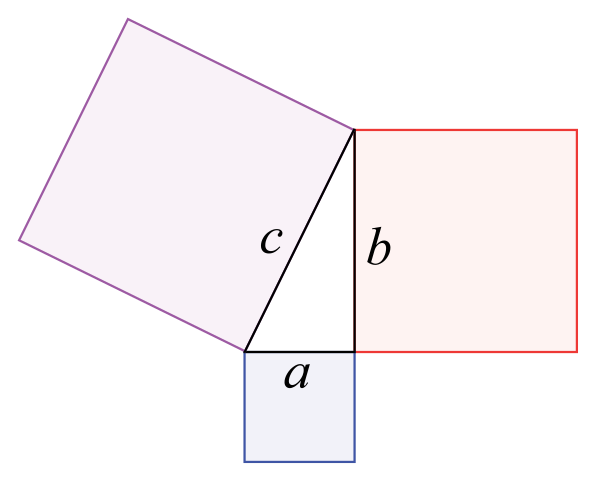

Pythagoras' theorem. Image: Wapkaplet.

In other words

$a^2+b^2=c^2.$

A right-angled triangle opined
My hypothenuse squared is refined
For if anyone cares
It's the sum of the squares
Of my other two sides when combined

The theorem is named after the ancient Greek mathematician Pythagoras of Samos, who lived between 569 and 495 BC, although it was already known to the Babylonians before him. For some beautiful visual proofs of the theorem, see this article.

Finding whales

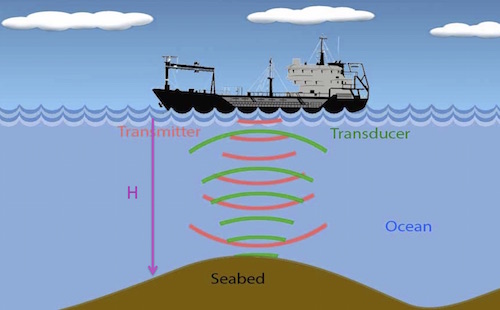
One very good way of locating fish and ships is active sonar, which involves sending out sound and listening to the echo. Whales, however, appear to hate the sound signals that are sent out. It confuses them and disrupts their behaviour; they have even been known to beach themselves to avoid the sound.

The answer is, not to send sound out into the ocean, but to listen for the sounds emitted by the whales themselves — to listen to the whales sing.

If a whale is swimming near the surface of the ocean a distance $L$ away from the ship, then the time $T$ it takes for a sound from the whale to reach the ship is

$T=L/C,$

where $C$ is the speed of sound in seawater, around 1500 metres per second. Our task is to find $L$ . But how?

The trick is to listen for two sounds: one that arrives from the whale directly and an echo of the sound from the sea bed. From this difference we will be able to work out the distance $L$ of the whale, but first we need to establish the depth of the ocean in the vicinity of the ship. This can be done using active sonar: send a pulse of sound directly downwards and listen for its echo. Below is a recording of the pulse and its echo, represented by their waveforms. The pulse itself is marked by the blue arrow and its echo by the red arrow.

In the time $D$ it takes the pulse to travel to the sea floor and back, it travels a distance of $2H$ where $H$ is the depth of the ocean.

This means that

$D=\frac{2H}{C}.$

Rearranging gives

$H=\frac{CD}{2}.$

Since we can measure $D$ and know the value of $C$ we now also know the value of $H$ .

Now let’s go back to Pythagoras’ theorem. By listening out for the whale’s song we can measure the time difference $\Delta$ between the arrival of a pulse of sound coming from the whale directly and a pulse emitted at the same time, but being reflected off the sea floor. This is done by listening to a whole range of echos and exploit the regularity, using statistical techniques.

The location of the ship, the location of the whale, and the point at which the whale’s sound bounces off the sea floor form a triangle, which can be divided into two right-angles triangles as shown in the diagram below.

Applying Pythagoras’ theorem to one of these triangles gives

$S^2=H^2+\frac{L^2}{4},$

$S=\sqrt {H^2+\frac{L^2}{4}}.$

The total distance travelled by the sound that bounces off the sea floor is $2S$ which, as we now know, can be written as

$2S=2\sqrt {H^2+\frac{L^2}{4}}=\sqrt {4H^2+L^2}.$

The time it takes for the echoing sound to travel from whale to ship is therefore

$T_{echo}=\frac{\sqrt {4H^2+L^2}}{C}.$

The difference between $T$ , the arrival time of the sound $T$ that arrives directly from the whale, and the sound $T_{echo}$ , the arrival time of the sound that bounces off the sea floor, is

$T_{echo}-T=\Delta = \frac{\sqrt {4H^2+L^2}}{C}-\frac{L}{C}.$

We can work out $L$ from this expression by first adding $L/C$ to both sides, so

$\Delta +\frac{L}{C} = \frac{\sqrt {4H^2+L^2}}{C},$

and then squaring both sides to get

$\Delta ^2+2\Delta \frac{L}{C}+\frac{L^2}{C^2} = \frac{4H^2+L^2}{C^2}.$

Subtracting $L^2/C^2$ from both sides gives

$\Delta ^2+2\Delta \frac{L}{C} = \frac{4H^2}{C^2},$

$L=\frac{2H^2}{\Delta C}-\frac{\Delta C}{2}.$

Since we know both $H$ , $\Delta$ , and $C$ , as well as the direction of the whale’s singing, we know exactly where the whale is. Changing direction, if necessary, we can save it from being hit.

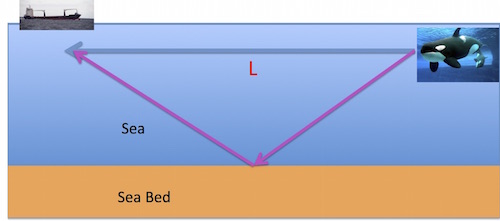
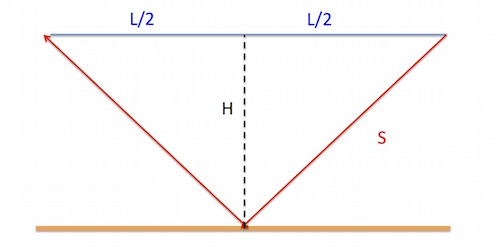
Thank you Pythagoras!

Chris Budd will give a talk about this subject at New Scientist Live in October 2019.

About the author

Chris Budd.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.

Comments

Sonar

Permalink Submitted by Hipassus on May 28, 2019

(1)

"One very good way of locating fish and ships is active sonar, which involves sending out sound and listening to the echo. Whales, however, appear to hate the sound signals that are sent out. It confuses them and disrupts their behaviour; they have even been known to beach themselves to avoid the sound.

The answer is, not to send sound out into the ocean[.]"

(2)

"[B]ut first we need to establish the depth of the ocean in the vicinity of the ship. This can be done using active sonar: send a pulse of sound directly downwards and listen for its echo."

I don't suppose the world will stop sending sound out into the ocean, as suggested in (1) (as much as we might wish) so I appreciate very much the use of mathematics to try and reduce the silencing of whales from one another that we cause.

However, I wonder if this does not simply mean whales are more likely to get a concentrated blast if they are more directly below us? That is a genuine question. I do not know anything about how sonar propagates in water. Does firing straight down reduce the total area affected by our sonar?

Thanks for this article and your work to help us humans be a little less awful to other creatures who share the planet with us.

Finding the depth

Permalink Submitted by Chris Budd on August 14, 2019

This is a fair comment. However, if you look at not just one reflected wave, but the time that the wave arrives after several reflections, then it is possible to find where the whale is without measuring the depth directly. In fact you find the depth as part of the calculation. I will leave this calculation to the readers of Plus