Tasty maths

The healthy English breakfast.

Mathematics is often used to study evolution, whether that be the evolution of animal species, the evolution of viruses or the evolution of language. A recent study has taken this one step further by modelling the evolution of national cuisine, and it was found that even though there are wall-to-wall celebrity chefs on television these days trying to broaden our culinary horizons, our cultural cuisines are largely the same as they were almost 100 years ago.

The paper The non-equilibrium nature of culinary evolution, published in the Institute of Physics' New Journal of Physics, shows that three national cuisines — British, French and Brazilian — have their own idiosyncrasies that have remained largely unchanged over time, despite many other cultural changes in the countries. Osame Kinouchi, Adriano J. Holanda and Antonio C. Roque from the Departamento de Física e Matemática, Rosa W. Diez-Garcia from the Departamento de Clínica Médica, and Pedro Zambianchi from Faculdade Bandeirantes — all from the University of São Paulo — compiled statistics on national culinary traits by examining recipes from the medieval cook book Pleyn Delit and three authoritative cook books from Britain, France and Brazil — The New Penguin Cookery Book, Larousse Gastronomique and Dona Benta respectively.

The authors found that national cuisines are affected by the founder effect, an effect most often concerned with biology. In biology, the effect refers to the loss of genetic variation when a new colony is established by a very small number of individuals from a larger population. Traits that may be unpopular within the larger group as a whole may become more established in the new group if its founders randomly had a higher proportion of that trait. For example, imagine a population of ants is 90% brown and 10% yellow. If a new colony of ants is founded by a random collection of 5 brown and 7 yellow ants who get separated from the main group, the new colony will have more yellow ants than the original group — there is a nice animation of this on the Evolution website. In terms of food, the founder effect explains why some idiosyncratic ingredients occur and perpetuate in the national cuisines.

The authors examined time, the number of ingredients and the number of recipes published in each cook book as variables to assess how diets have evolved. By using three editions of the Brazilian cook book Dona Benta (from 1946, 1969 and 2004), they found that the rank and importance of idiosyncratic local ingredients, such as chayote, remained much the same despite the change in Brazil from a regional food profile to a more globalised cosmopolitan profile. The authors said of these occurrences: "Some [improbable] ingredients present in the initial recipes have a strong difficulty of being replaced and can even propagate during culinary growth. They are like frozen 'cultural' accidents."

The researchers found that the statistical hierarchy of ingredients in each country's cook book can be represented by Zipf's law. Zipf's law arose out of an analysis of language by linguist George Kingsley Zipf, who theorised that given a large body of language (that is, a long book — or every word uttered by Plus employees during the day), the frequency of each word is close to inversely proportional to its rank in the frequency table. That is: \ $$P_n\propto 1/n^a$$ where a is close to 1. This suggests that the most frequent word will occur approximately twice as often as the second most frequent word, which occurs twice as often as the fourth most frequent word, etc. A famous study of the Brown Corpus found that its words accorded to Zipf's law quite well, with "the" being the most frequently occurring word (accounting for nearly 7% of all word occurrences — 69,971 out of slightly over 1 million), and "of" the second most frequent (3.5% of all words). The São Paulo authors found that this statistical distribution holds true for each cook book with the idiosyncratic ingredients having higher positions in their national lists. The rankings of ingredients in the Brazilian cook book remained stable over time, despite the cultural changes of the country. By comparing ingredients with similar rankings across the cook books the authors concluded that national menus evolve in similar ways.

So, next time you are tucking into your English breakfast, Aussie BBQ, American hamburger, German sausage or Canadian pancake, don't feel so bad — there are evolutionary reasons for eating such fatty food!

Plus extra:

Never one to turn down a challenge, Plus set about seeing if the frequency of words on all Plus pages matches the Zipf distribution. As you can see in the chart below, it fits remarkably well! The most popular word on Plus is "the". "The" is mentioned 114001 times, or 6.86% of all words. Second in line is "of" occurring 62964 times, and third is "to", occurring 45045 times. Unsurprisingly, the word "maths" features more highly than in normal usage, coming in at 40th place having been mentioned 4829 times. "Mathematics" is at 51st and "mathematical" at 54th. "Plus" comes in at 76th, having been mentioned 2454 times. Only words mentioned more than 10 times were plotted.

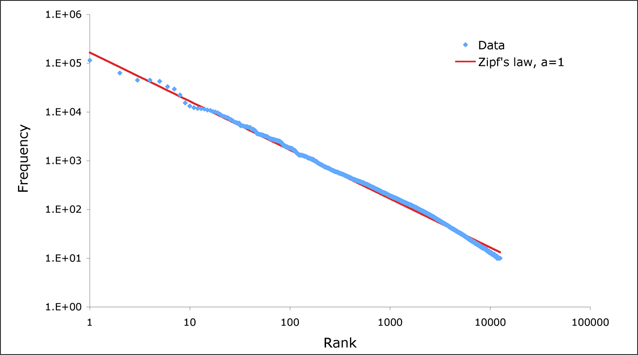
The frequency of words on Plus fit the Zipf distribution very well.

A similar test has been done on word usage in wikipedia. It was found that Zipf's law holds true for the top 10000 words.