
A tip of the hat: Celebrating an aperiodic monotile
Last year in March the world of maths was thrilled by an announcement that even made it into the mainstream news. David Smith, a mathematical hobbyist, had discovered a beast that had eluded mathematicians for some time: an aperiodic monotile, also known as the hat or an einstein.
Just before Christmas we were lucky enough to meet David and two of the mathematicians who helped put the discovery into context. So we will start the new year by looking at the hat, its discovery, and some creative ways in which people have made it their own.

The hat is an aperiodic monotile, also known as an einstein.
Start in the bathroom
To understand the hat, start by thinking about bathroom walls. They are usually tiled with square tiles. In theory you could continue such a tiling in all directions indefinitely — you could tile an infinite bathroom wall using squares.

A piece of the two dimensional plane tiled by squares. The pattern is periodic.
Such a tiling is repeating; to use the mathematical term, it's periodic. If you were to pick the whole thing up, move it to the left or right by the width of a tile, and then put it down again, the pattern you'd see would look exactly the same as what you saw to start with. The same would apply if you moved it up or down by the height of a tile, and even if you moved it diagonally in the directions indicated by the diagonals of the squares.
You can make periodic tilings with other shapes too. Triangles or regular hexagons, for example. You can also make a periodic tiling with several different shapes. (Strictly speaking, to be periodic a tiling only needs to repeat in two opposing directions such as left/right or up/down. It doesn't need to repeat in other directions too.)
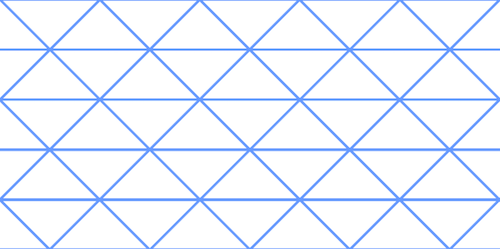
Tilings of the plane by triangles (top) and hexagons (bottom).

This is an Egyptian pattern. It's periodic and made up of several different shapes. Image from The Grammar of Ornament (1856). Egyptian No 7 (plate 10), image #8. (Public domain)
The question that interested mathematicians who like tilings was whether you could find a single shape that can tile the entire plane (without overlaps or gaps) and for which the pattern you produce is not periodic. If you pick such a pattern up and move it along in any direction by any distance, the picture you see will never look the same as what you saw to start with.
If you think about this for a while and play around with the kind of shapes that naturally spring to mind, you'll see that such a shape of tile is hard to find. Unless you happen to hit on the hack shown below, where a generally periodic tiling contains one small defect that breaks the periodicity.
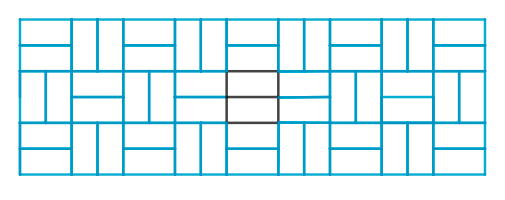
A piece of a tiling by a rectangle placed horizontally or vertically in an alternating pattern. If the pattern is disrupted by a couple of rectangles that are out of sync (the black ones), then this ensures that the overall pattern is not periodic.If you shift it in any direction, the out-of-sync patch will always end up in a new location, so the pattern can't look the same as it did before.
This hack feels like cheating, which is why mathematicians excluded it from their search. They defined an aperiodic tiling to be one that doesn't contain arbitrarily large periodic patches — this means it's properly aperiodic, not just a periodic tiling with one or more small defects.
An aperiodic monotile is a single tile that can form an aperiodic tiling of the entire plane. It's such a tile that David Smith discovered. It's called the hat because it looks a bit like one (though if you turn it around it looks like a T-shirt). The reason it's also called an einstein is nothing to do with Albert, but with the fact that "ein Stein" is German for "one stone".
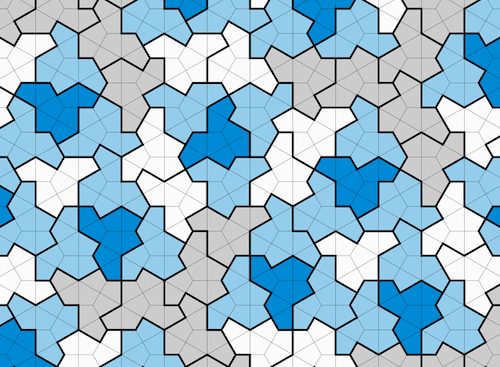
A patch of an aperiodic tiling by hats. Image by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, CC BY 4.0 Deed.
People have been thinking about aperiodic tilings for a long time. Relevant ideas appear in the work of the 16th century artist Albrecht Dürer and the 17th century polymath Johannes Kepler. In the 1970s the eminent mathematician
.svg.png)
A patch of a Penrose tiling using six different shapes. (Public domain)
.svg.png)
A patch of a Penrose tiling using two shapes, a thin and a fat rhombus. (Public domain)
Smith's discovery of a single shape that can tile the plane aperiodically is considered a huge breakthrough. And it's not just of interest to people who enjoy forming patterns. Aperiodic tilings can be used to understand quasicrystals, types of crystals that were discovered in 1982 by Dan Shechtman and earned him the 2011 Nobel Prize in Chemistry (find out more here).
Caught in the wild
There are mathematicians who devote a large part of their time to investigating tilings. One of them is Craig Kaplan, strictly speaking a computer scientist, who wrote us an article about tilings back in 2007. (The article contains some important ideas relevant to aperiodic tilings, such as that of substitution rules.) Kaplan, like most other people working in the field, uses computers to investigate tilings, which makes things a lot easier than cutting shapes out of cardboard.
Hat discoverer David Smith, however, is not a professional mathematician and doesn't normally use computers to play around with tiles. Instead, he uses machine-cut tiles made out of card. Having thought of the hat and seen interesting patterns emerge when putting copies of it together, Smith contacted Kaplan to see if software could produce larger patches of tiling than Smith was able to create manually. Kaplan soon "caught hat fever" and experimented with hat tilings using computation and digital drawings. Within a few weeks he was convinced the hat could indeed tile the plane aperiodically — that it was an einstein. (See this interesting interview with Kaplan by Tim Chartier for more information.)
What was needed next was a proof. Since you can't possibly tile the infinite expanse of the plane in practice, you can never be sure the overall pattern you'd get if you could is not periodic. It might be that the patch of the tiling that repeats is much larger than any patch you can produce in your lifetime, so you'd never get to see the repetition. Only a mathematical argument which shows conclusively that the tiling is aperiodic can give you certainty.
To provide the "mathematical muscle" needed for a proof, Kaplan and Smith contacted mathematician Chaim Goodman-Strauss, who'd been working on tilings for decades. "I immediately suggested they bring in Joseph Myers," Goodman-Strauss told us when we met him at the University of Cambridge, where he gave a talk about the hat with Smith and Myers in the audience. "I was sceptical about [the hat] at first, but Joseph was our secret weapon. Normally [proofs] like this might take months, but within about a week of being contacted Joseph produced the first of two proofs [of the hat being an einstein]." (You can see the relevant paper by Smith, Myers, Kaplan, and Goodman-Strauss here.)
What Smith did, says Goodman-Strauss, is akin to catching a never-before-seen animal in the wild. When mathematicians search for tiles with particular properties, they carefully design them, just like you might purposefully breed an animal with the characteristics you'd like. Smith, however, went out looking in the field. He knew roughly where he might find the fabled beast, but the fact that it was actually there couldn't have been predicted.
Had Smith been a professional mathematician, says Goodman-Strauss, he might not have been able to do this. "It would have been very foolish for someone who needs to [fulfil professional duties] to even tackle a problem like this, much less to spend the time doing what Dave did, which was to methodically investigate example after example. The structural forces of academia would have made this very difficult."
A life of its own
Tilings have an aesthetic appeal, as well as a mathematical one. One person who has taken the latest discoveries as artistic inspiration is our good friend David Spiegelhalter, Emeritus Professor of Statistics at the University of Cambridge. "These shapes are a great discovery, all the more extraordinary coming from David Smith working at home," says Spiegelhalter. "I had the huge honour of meeting him this summer in his hometown of Bridlington, Yorkshire, and was inspired to try and make a spectre tiling in stained glass." The result was displayed at Goodman-Strauss' talk to be admired by the audience. (A spectre is a type of tile, also discovered by David Smith, that is related to the hat, see below.)

David Spiegelhater's stained glass version of a spectre tiling. "I can't cut sharp concave angles, and so had to break the spectre shape into convex components, but fortunately I could copy a wonderful decomposition into a triangle and five identical 'cairo' pentagons," he says.
The reason Smith, Myers and Goodman-Strauss found themselves together in one place was that the day before their visit to Cambridge they'd been to the House of Commons in London for the award ceremony of a very special competition. The Einstein Mad Hat Awards were launched jointly by the UK Maths Trust and the National Museum of Mathematics (MoMath) in New York in September 2023, enabled by support from XTX Markets. The aim of the competition was to find the most creative use people could think of for the hat.
The results are truly amazing, with entries ranging from hat shaped ravioli (a winning entry by Evan Brock) to dinosaur designs (an entry by Alec Dixon which received an honourable mention). You can see these below and all winners and honourable mentions on the MoMath website.
"What was so moving and significant to me was that people made this their own," says Goodman-Strauss. "They took on the hat as something they owned and that they will pass on and share with other people. It's absolutely unique, in my experience, for a mathematical result to have a cultural life like that."

Ravioli hat tiling, winning entry of the Einstein Mad Hat competition by Evan Brock. Yummy! (Image used by permission.)

A dinosaur design based on the hat by Alec Dixon, which received an honourable mention. Dixon studied Zoology at Cambridge and got hooked on tessellating dinosaurs in the late 80s while teaching in primary schools. (Image used by permission.)
An observation for sharp eyes
If you have had a very close look at the tiling by hats shown above, you might have noticed that every now again the mirror image of the hat is used, rather than the hat itself. Without this mirror image the hat isn't able to tile the plane. The ratio between hats and mirror hats in the tiling is about 7 to 1.
Mathematicians don't care about this that much: since the operation of turning the hat into a mirror hat is a simple reflection, the two shapes are often considered the same in this context. And indeed, if you cut copies of the hat out of card, then simply flipping a card over will turn the hat into the mirror hat.
Some people have suggested, however, that the need for a mirror hat means that the tiling requires two different shapes. There's good justification for that too: if you use ceramic tiles that are glazed on one side, flipping over wouldn't be possible so you'd need two templates to cut the tiles from.
This might feel a little anticlimactic, but there's a happy ending. A couple of months after announcing the discovery of the hat, the team found another tile, actually a whole family of tiles, called spectres, each of which can single-handedly tile the plane aperiodically without need for mirror images. Phew!

A patch of tiling by a spectre tile, which has curved edges. Image by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, CC BY 4.0 Deed.
About this article
Chaim Goodman-Strauss is Outreach Mathematician at MoMath. He gave a talk at the Centre for Mathematical Sciences in Cambridge in December 2023 with David Smith and Joseph Myers in the audience. Marianne Freiberger, Editor of Plus, interviewed Goodman-Strauss after the talk.