
Women of mathematics: Natalia Berloff
This article, the video and the podcast accompany the Women of Mathematics photo exhibition. You can download Natalia Berloff's exhibition poster by clicking here. To see more profiles of female mathematicians and to find out more about the exhibition, see here. Photographs by Henry Kenyon.
Watch the interview with Natalia Berloff in this video!
Natalia Berloff is a Professor of Applied Mathematics at the Department of Applied Mathematics and Theoretical Physics, University of Cambridge, and a Fellow of Jesus College.
Plus: How and when you chose to do mathematics?
Natalia Berloff: Aged about 10, the usual age for this kind of thing. It just happened. I was reading tons of books, shelves after shelves. On one shelf, there were a lot of books about mathematics, some were for children, for example one explaining graph theory. I was suddenly, completely taken by the theory, by how logic works to actually solve unsolvable problems on graphs, so that was the beginning.
I grew up in Russia, so we had a very well developed Olympiad movement in mathematics. I started winning on various levels, and once you get to the country level, then big players like Moscow State University and Landau School start taking notice of people, so that's how I got lured into this wild world.
Plus: What's it like being a female mathematician?
Natalia Berloff: Being a mathematician – female or male – I don't know if it makes such a big difference. We're defined by our profession.
Plus: Is there any advice that you would give to a young woman wanting to enter mathematics, or do you think the advice is equal for both genders?
Natalia Berloff: I think it's equal. I have a boy and a girl, a son and a daughter, so I give them the same advice. The advice is that being good in maths opens a lot of possibilities. You don't have to be a mathematician, but knowing mathematics opens the road for any science; physics, chemistry, biology. You can do whatever you want.

Plus: For you, what are the joys of doing mathematics, and what are the challenges?
Natalia Berloff: It' a treasure hunt. That's exactly what we do. We're trying to find our jewel, to find the treasure, in a sense we that have some leads. We're solving the problem, and there are hints, leads, but you need to find this holy grail, and then you start using different tools. You start learning different tools, different machinery that probably will help you to discover.
Also, I think at first, when you start being in mathematics, or in physics, you start finding these little jewels, these little things, and you're very happy. The more you go, the more you are really looking for a big thing, and that's what the excitement is about, just expecting that you'll have this big breakthrough.
Plus: Could you explain your area of mathematics?
Natalia Berloff: It's applied mathematics, so I'm writing equations and trying to understand a physical system. In my case, quantum fluids, superfluidity, Bose-Einstein condensate, and for a given physical system, it could be liquid, it could be gas, it could even be a solid state, I'm trying to write down the equations that describe the motions, that describe the phenomena observed.
I'm in close contact with experimentalists, trying to see if my theory works, and what else they present that still doesn't fit into the model, so I can extend it and build a new one.
Plus: Could you describe one of your favourite mathematical moments?
Natalia Berloff: There were many. The first one, again, was in this book that I mentioned, that I read when I was 10. There was this problem of a given set of points, a graph as a set of points with edges in between — a network. Is it possible to go along every edge just once, without taking your pen off the paper? A very simple problem. The answer is brilliant, as it seemed to me when I was 10. The answer is you count every node, and how many passes are going out of this node.
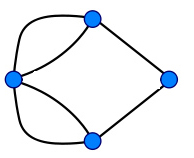
In this graph two nodes have an odd number of edges and two have an even number of edges. This means that you can find a path that crosses every edge exactly once. Image: Bogdan Giuşcă.
If the number is odd, it means that you will be able to start, go around, come, and leave. If it's even, then you can't go, come and go, which means that only the graphs where you have two nodes with odd numbers will actually satisfy the property that you can go across every edge exactly once. You have to start at the first odd and finish at the other one. That was a very simple answer. Before knowing the answer you try various graphs, and you see that sometimes you don't know why it works, or why it doesn't work. Maybe you just didn't find the right way. At the end, when you understand, it makes perfect sense. Then, you think, "Oh, wow. Now I can solve any problem because I know this trick." For me being 10, that was a memorable moment. (You can find out more about this problem in this article.)
Plus: Thank you very much!