
The Abel Prize 2019
Karen Keskulla Uhlenbeck has been awarded the Abel Prize 2019 for her pioneering work in geometry, analysis, mathematical physics and more. The Abel Prize is awarded every year for outstanding scientific work in mathematics. Uhlenbeck is the first woman to receive it in its 16-year history.

Karen Uhlenbeck giving a talk at the Institute for Advanced Study. Photo: Andrea Kane.
Uhlenbeck's body of work covers a dizzying array of areas. "Her strength is the great breadth of her work and interests," says Simon Donaldson, winner of the 1986 Fields medal for work that incorporated some of Uhlenbeck's ideas. "Much of her work has a truly pioneering quality [...] one could imagine it might never have been done otherwise."
Blowing bubbles
One pioneering thread in Uhlenbeck's work starts with something surprisingly familiar: the fact that the shortest path between two points in the plane is a straight line.

The shortest path between A and B runs along a straight line. How could it be otherwise? Any other path is obviously longer!
Most of us just take this fact for granted — how could it be otherwise? — but it's also possible to prove it with full mathematical rigour. Given any path connecting the two points there's a formula giving you its length (for those who know calculus the formula is an integral). With a bit of manipulation you can find the path that minimises that formula. The proof belongs to an area called the calculus of variations, which is all about minimising or maximising some quantity subject to constraints.
Stepping up a dimension, a similar problem lands you in the beautiful world of soap films. The toys we use to blow soap bubbles come with a plastic frame to be dipped into soapy water. The soap film that forms within the frame after dipping has the smallest area possible. In theory you could imagine the film taking all sorts of shapes, it could contain bumps for example, but the flat shape it does take minimises area, and, equivalently, surface tension and energy — nature likes to be frugal.

Before we blow the bubbles the soap forms a film spanning the plastic frame (or in this case each of two frames!). Image: fir0002, CC.
A minimal surface is a surface that's made up of lots of surfaces that minimise area in this way: around any point you can draw a loop on the surface so that if you dipped that loop into soapy water the film you'd get would match the bit of the surface within the loop. For example, the entire two-dimensional plane can't be produced using soap (because it's infinite) but it still counts as a minimal surface because you can make it out of lots of over-lapping finite minimal surfaces you can get from wire frames.
Finding minimal surfaces is an incredibly difficult problem. Until the 19th century only three of them were known: the plane, the catenoid and the helicoid.

The helicoid. Photo © The Exploratorium.

The catenoid.
Chasing minimalism
Uhlenbeck did her PhD in the calculus of variations in 1966 and turned her attention to minimal surfaces when she met Jonathan Sacks in the 1970s. "I didn't know very much about minimal surfaces, but we talked about them and worked together," Uhlenbeck said in a 2018 interview with Allyn Jackson. "He brought the knowledge of the subject of minimal surfaces, and I brought the main idea [of the work]."
One way of defining a minimal surface, which is easier to deal with than area, is in terms of something called its energy (see the box below for a formal definition). Just as the length of a path between two points can be described by an integral, so can the energy of a surface. The task is to find a surface which minimises this energy formula.
When you are dealing just with paths the problem is relatively straightforward. A hugely helpful fact (in the setting Uhlenbeck and Sacks were considering) is that paths can bunch up, coming closer and closer to each other, until they eventually converge on a limit path.
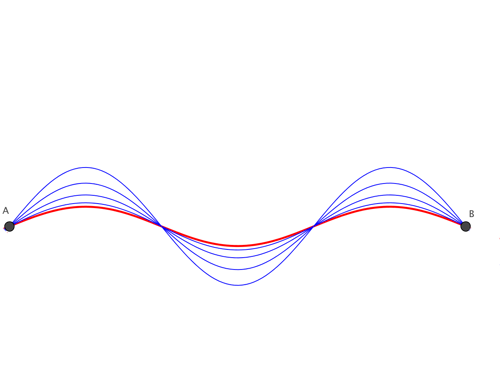
Illustration of blue paths converging on a red path. You can imagine infinitely many more blue paths getting closer and closer to the red one.
The concept of energy is intimately bound up with this convergence: if within a collection of smooth paths from A to B the energy of every path is smaller than some bound, then you can be sure that the collection contains a sequence of paths that converges to a continuous limit path from A to B. Since the overarching problem is to wrestle a minimal path from the infinity of all paths connecting A and B, it's not surprising that this kind of compactness result (called compact because there are limits) is important.
When it comes to surfaces, however, energy isn't quite strong enough to give you a similar result. The problem lies with the many ways you can use to describe a surface. As a loose illustration, imagine a surface that looks like a deformed sphere; a knobbly potato, for example, or a deflated football. To find your way around such a wonky surface you might construct a map from a round sphere: every point on the round sphere is associated to a point on the deformed sphere. This is exactly what we do when we represent the less-than-perfectly-spherical Earth by a map on a round globe. There are, however, many different choices of which point on the sphere to associate to which point on the surface, so there are many different choices of map.

A sphere can serve as a map of the surface of a potato if every point x on the potato is associated to a point on the sphere. There are however many different choices of how to associate points, so there are many different maps.
Perturbing energy
In Uhlenbeck and Sacks' mathematical world, surfaces living in 3D space (or any other manifold) are also described by certain kinds of maps. In this context the formula that gives you the energy of a surface doesn't necessarily care about the kind of map you use, in particular, it doesn't see distance scales. When it comes to sequences of maps, however, scale can be important: it can mess up the convergence of maps, and therefore deprive you of the kind of compactness result you need to show that minimal surfaces exist. (You can find out more about this kind of maths in this article.)
Playing with energy
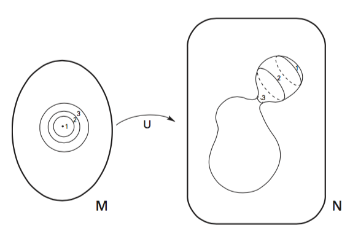
Given two compact manifolds $M$ and $N$ and a smooth map from $M$ to $N$, the energy $E$ of the map is given by the formula $$E(u)=\int_M |\nabla u|^2,$$ where $|\nabla u|$ is the standard norm defined by the metrics on $TM_x$ and and $TN_{u(x)}.$ The slightly varied energy expressions Uhlenbeck and Sacks were looking at have the form $$E_a(u) = \int_M (1+|\nabla u|^2)^\alpha,$$ for $\alpha>1$.In a landmark paper, Uhlenbeck and Sacks found an ingenious way to remedy this problem. They tinkered with the usual expression for the energy of the surface to obtain expressions that are ever so slightly different (see the box). These new expressions can see scale and therefore regain the strength to prove a compactness result. This means that for each of these slightly varied expressions you can find a meaningful minimising map. You can construct a sequence of slightly-varied energy expressions that converges on the original energy expression. Each of the slightly varied expressions comes with its own minimising map, so the idea is to see whether these minimising maps converge to anything meaningful regarding the original energy expression.
Uhlenbeck and Sacks showed that they do, at least mostly. The sequence of minimising maps may not converge at some points on the sphere on which they are constructed, but there are at most finitely many such points and it's still possible to describe what happens there: rescaling the maps within small regions around the awkward points, you find that the regions are blown up to what you might call "bubbles" in the surfaces the maps describe. You can find out more in Simon Donaldson's excellent article about Uhlenbeck's work.
A schematic of bubbling: small regions around an awkward point are blown up into bubbles. Illustration from the Notices of the American Mathematical Society.
This idea of rescaling the problem is what Uhlenbeck called her "main idea" and it allowed Uhlenbeck and Sacks to prove important results about the existence of minimal surfaces. It finds applications in many other problems too. "A lot of problems that are totally geometric [do not care about scale]," Uhlenbeck explained in her interview with Jackson. "If you have a problem where you are looking for a metric, and somehow or other, there is no intrinsic external scale on it, you can actually change the scale that you are looking at."
Beyond soap
The ideas of Uhlenbeck and Sacks have spawned a large body of subsequent work in several areas. "[their] work on minimal surfaces has been the foundation for huge further developments over four decades," says Donaldson. Amazingly, one such development involves an area of physics that goes way beyond soap films: the attempt to create a theory of everything that not only describes phenomena we can see, but also explains the world at very small and very large scales we will never experience.

Karen Uhlenbeck is the first woman to win an Abel prize.
As Uhlenbeck has noted, "No one plays with quantum effects as a child," so the concepts involved here are not quite as intuitive as they are for soap. But there are mathematical similarities between the theory of minimal surfaces and the quantum physics described by so-called gauge theory. As Uhlenbeck wrote: "It is a powerful mathematical fact that intuition and techniques can be passed back and forth between [the theory of minimal surfaces and gauge theory]."
Inspired by the late, great Michael Atiyah, in the late 1970s, Uhlenbeck turned her attention to the theory which underlies our understanding of particle physics, called Yang-Mills theory. As physicists struggled with the maths Uhlenbeck pioneered the study of the the Yang-Mills equations from a rigorous mathematical point of view, discovering bubbling phenomena and notions of compactness in the process. Her work in this area laid the foundations of all subsequent work in gauge theory. Her work on instantons was similarly inspired by question from physics but ended up revolutionising pure mathematics and led to a seminal textbook, written with Dan Freed.
The study of gauge theory, initially an "adopted child" of mathematics (as Uhlenbeck called it) has not only benefited physicists, but also in turn fed back into pure maths. It has led to results that may never have come about without the physical inspiration.
"I am definitely very attracted to the idea that there are a lot of different facets in mathematics and seeing the connections," Uhlenbeck said in her interview with Jackson. "I would be very interested in learning a lot more about things that are not core mathematics, but are mathematics connected with other areas." It's great to see her win the Abel Prize for the connections she has already made. We have only given a small glimpse of them here and wish her the best of luck with her pursuit of others still to be found.
Congratulations Karen Uhlenbeck!