
The Abel Prize 2025: Masaki Kashiwara
The Abel Prize 2025 has been awarded to Masaki Kashiwara, of Kyoto University, Japan, for
"his fundamental contributions to algebraic analysis and representation theory, in particular the development of the theory of D-modules and the discovery of crystal bases."
The Abel Prize is one of the most prestigious honours in mathematics. It is awarded every year by the Norwegian Academy of Science and Letters and comes with a prize money of over £550,000.
Kashiwara's work, as that of many outstanding mathematicians, bridges worlds. At school we're usually taught that maths splits up into different fields: geometry, algebra, and calculus, for example. In reality, though, they are all linked — and it's often when someone finds a way of applying methods from one area to another that mathematics opens up to new advances.
Symmetries
To get a glimpse of the areas that Kashiwara's work has linked, start thinking about symmetries. We tend to think of symmetries in a visual way, as transformations that leave a shape unchanged.
As an example, you can reflect a rectangle in its vertical and horizontal axes, and you can rotate it by 180 degrees, without changing the way it looks. These operations, together with the operation of doing nothing at all, are the symmetries of a rectangle.
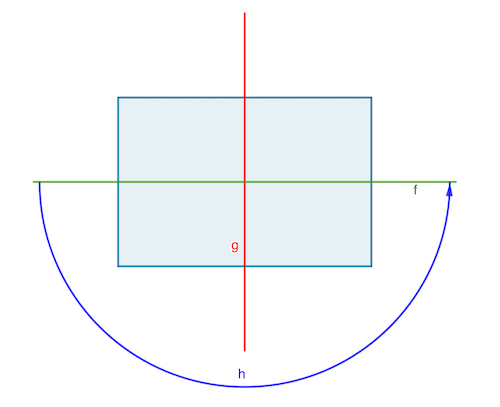
The symmetries, when taken altogether, form a self-contained system. When you follow one symmetry by another, the result is also a symmetry: for example, reflecting in the horizontal axis and then reflecting in the vertical axis amounts to rotating the rectangle by 180 degrees (you can see this by labelling the corners of the rectangle and seeing where they end up in each case). Every symmetry in this collection can also be "undone": in our example, doing an individual symmetry twice puts every point on the rectangle back to where it started.
The structure within the collection of symmetries means that they form what mathematician call a group (a group is defined by a particular set of rules, see here for the details).
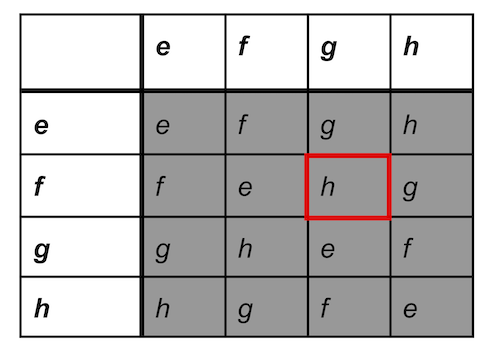
Keeping track of what you get when doing one symmetry after another is a little tedious, but you can make yourself a handy table, as the one shown below. Labelling the reflections and the rotation as in the image above, the entry corresponding to, for example, the row labelled f and the column labelled g tells you what overall symmetry you get when you apply g followed by f — in this case it's h.
Leaping into abstraction
Now here's a thing. You may find other mathematical objects which are not (to the untrained eye) symmetries of anything, but that can also form groups. Examples are matrices, arrays of numbers that can be multiplied together so that the result is always a matrix too. When you label the members of such a collection by letters and construct a table as we did above, you may find that the table looks exactly the same as the one coming from the symmetry group of a rectangle.
This offers a chance for a wonderful leap into abstraction — you can think of groups, not as collections of particular things, but as collection of abstract objects that interact in a way prescribed by a table of letters. What defines the group is not the nature of the things that make it up, but the way they interact.
What you're doing now is algebra. You're investigating the structure of collections of abstracts objects. There are also other types of collections with different types of structure. For example, in a mathematical ring you don't just have one way of combining two of your abstract objects, but two (you can think of them as akin to addition and multiplication of numbers).
The power of this abstraction lies in the fact that, once you know something about your abstract collection of things, this knowledge applies to any collection of concrete things that embodies it — be they the symmetries of a shape, matrices, or anything else that fits the picture.
A changing world
From these lofty heights of abstraction let's now come back down into the real world. It is to a large extent characterised by change — things move, they grow, and they evolve in other ways too. We can try to describe this change mathematically and use the description to make predictions: if you have observed that the money in your bank account grows by £1000 every month (lucky you) then you can use it to predict that in a year's time you'll be 12 x £1000 = £12,000 better off.
In this example a simple change happened once a month. Usually though change happens on smaller timescales, even instantaneously (imagine all your money invested in an ever-changing stock market). In maths such change is described by differential equations. These equations describe the rate at which a quantity changes — over time, or perhaps over space, or with respect to some other reference quantity.
To make predictions you need to solve the differential equation that describes the change. The solution will tell you how big the quantity in question will be at a given point in time (or space or for a given value of your other reference quantity).

Differential equations crop up pretty much whenever you're applying maths to solve real-world problems — in physics, biology, chemistry, economics, and engineering, to name just a few fields. The trouble is that the equations tend to be complex beasts and can be incredibly hard, even impossible, to solve. (You can find out a little more about differential equations in this brief introduction.)
To mathematicians this difficulty is fascinating. This is why differential equations form a field of study in their own right. People investigate them without reference to the real-life problem they arise in, and they even investigate equations that don’t arise from any real-world problem. The tools used here are those you meet in calculus: to get to grip with change you need to look at infinitesimal quantities, limits, and the like.
The field of mathematics which gives the tools from calculus a formal basis, making sure everything is logical, correct, and proved, is called analysis.
Algebraic analysis
As we've introduced them the two areas, algebra and analysis, appear quite different — algebra lofty and abstract and analysis somewhat more intricate and (apologies to analysts) messy. But appearances deceive and there are important links.
Analysis deals with mathematical objects such as functions. An example is the function $f(x)=1000x,$ which we met above, expressing the amount of money you'll have gained after $x$ months if your wealth increases by £1000 a month.
Viewed as mathematical objects functions can be combined (for example you can apply one function after another, with the overall result being also a function), so you can look at collections of functions just as we looked at collections of symmetries above. Such collections can also form algebraic structures like groups or rings. The same goes for things like differential operators, which relate functions to rates of change.

This creates a link between algebra and analysis. The field of algebraic analysis exploits this link to tackle problems concerning differential equations using algebra. People have been exploiting the power of algebra in this context for quite a long time, but credit for establishing algebraic analysis as a systematic field of study goes to the Japanese mathematician Mikio Sato.
Kashiwara met Sato at the University of Tokyo in the 1970s and completed his Master's thesis under Sato's supervision. In this thesis, and at the tender age of 23, Kashiwara developed the theory of D-modules. These objects, essentially algebraic structures related to differential equations, became a fundamental component of algebraic analysis and have proved an amazingly powerful tool in many areas of mathematics. (If you'd like a technical introduction, you can read a beautiful translation of Kashiwara's Master's thesis.)
An important example of the kind of avenues that D-modules have opened up comes from a problem posed by the mathematician David Hilbert in 1900 at the International Congress of Mathematicians in Paris. The Riemann-Hilbert problem was the 21st on a list of 23 problems Hilbert thought would set the research agenda for twentieth century mathematics. Within the general spirit of analysis, the problem asks whether there is a class of differential equations that all satisfy a specific set of characteristics.
While the simplest version of the problem was solved by others, Kashiwara formulated and proved results in a vastly generalised setting than that originally proposed by Hilbert. You can read a little more in our article on Kashiwara's work written by Rachel Thomas in 2018 on the occasion of Kashiwara winning a Chern Medal. Kashiwara still works on this area today and, together with Andrea D'Agnolo, has not long ago made important extensions to his work resulting from the Riemann-Hilbert problem.
Representing abstract structures
Kashiwara's work inspired by the the Riemann-Hilbert problem links up with representation theory, the other area mentioned in the quote from the citation above, besides algebraic analysis.
Representation theory brings us nicely back around to the beginning of this article when we were thinking about algebraic groups. We noted that groups can be thought of as collections of abstract things. We don't need to know what exactly these things are — it's the way they interact that defines a group.
This abstraction is lovely but can also be a little too loose. When working with a group it can be useful to know what exactly those things are that make it up. And when working with more than one group it might be useful if the things that make them up are of the same type — it's hard to compare apples with oranges.
Mathematical nature has been kind to mathematicians in this respect. It turns out that many groups, particularly those made up of finitely many things, can be thought of as being made up of matrices: those arrays of numbers we already mentioned earlier on (see here to find out more). For example, reflections and rotations of the plane, such as those that give the symmetries of a rectangle, can be represented by matrices that have four entries arranged in two rows of two. These can be interpreted as transformations of the plane (technically matrices can act on vector spaces).
More generally, when you are given an abstract group, there’s a good chance that you can find a collection of matrices that together form exactly that group. This is lucky because mathematicians understand matrices particularly well.
Representation theory is the study of groups, and other algebraic structures, in terms of matrices acting on vector spaces. (You can read more in our introductory article here.) It's a prominent field of study that is useful in many other areas of mathematics. Kashiwara's theory of D-modules has proved hugely useful in representation theory.
In another feat of making connections, and inspired by problems that originated in theoretical physics, Kashiwara also introduced to the idea of crystal bases to representation theory. These objects allow questions in representation theory to be answered in terms of combinatorics — the art of proving results by counting things. Crystal bases have also found applications in number theory and even in statistical physics. (You can read a little more in this article).
What we have given here is just a small flavour of the origins of Kashiwara's work and its profound implications for mathematics. The Abel Prize citation says,
"Kashiwara is an exceptionally prolific mathematician with more than seventy collaborators. For over fifty years he has reshaped and deeply enriched the fields of representation theory, in its numerous incarnations, and algebraic analysis. His work continues to be at the forefront of contemporary mathematics and to inspire generations of researchers."
Kashiwara will receive his Abel Prize from the King of Norway on May 20, 2025, in Oslo. Congratulations!
About the author
Marianne Freiberger is Editor of plus.maths.org.