
Why is the violin so hard to play?

When you pluck a note on a guitar string, there isn't very much that can go wrong. You may not play the right note at the right time, of course, but a single note will always come out at the expected pitch, and sounding reasonably musical. When a beginner tries to play a violin, things are much more difficult. When a bow is drawn across a string, the result might be a musical note at the desired pitch, but on the other hand it might be an undesirable whistle, screech or graunch. This difference stems from a fundamental distinction between the physics of plucked and bowed strings.
Linear versus nonlinear: plucked versus bowed
A plucked string, like that on a guitar, can be described by linear systems theory. The essential feature of a linear system is that if you can find two different solutions to the governing equations, then the sum of the two is also a solution. In the context of vibration, this idea has a direct physical application.
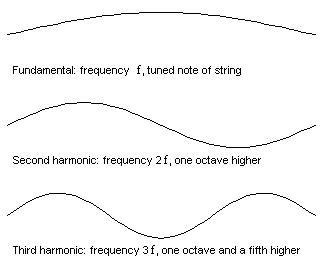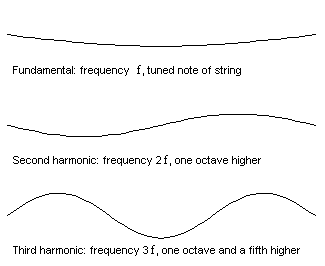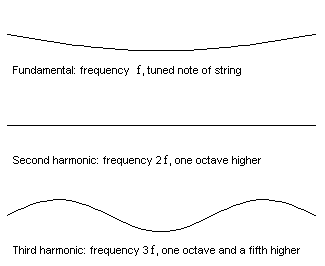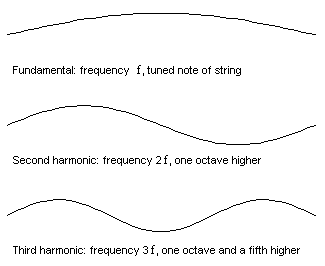
The first few vibration modes of a vibrating string...
A vibrating object like a stretched string has certain resonance frequencies, each associated with a particular pattern of vibration called a vibration mode. The corresponding resonance frequencies are the "fundamental" and "harmonics" of the note to which the string is tuned. If the string is set into vibration in the shape of one of these modes it will continue to vibrate in this shape at the corresponding resonance frequency, with an amplitude which gradually dies away as the energy is dissipated into sound and heat.
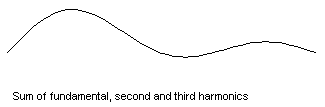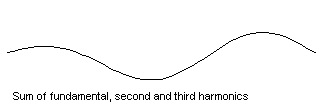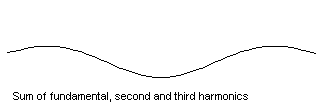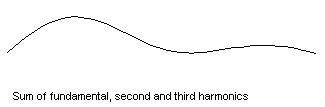
... and a string vibrating in all three modes at once
Now if the string is vibrated in a way that involves several of the mode shapes at once, then the principle of linearity comes into play. Each mode simply goes its own way, vibrating at its particular resonance frequency, and the total sound is the sum of the contributions from these separate modes (you can read more about adding harmonics in Music of the Primes in Issue 28). The guitar player can vary the mixture of amplitudes of the various modes, by plucking at different points on the string or using a different plectrum, but the set of resonance frequencies is always the same. In musical terms, the pitch of the note is always the same but the tonal quality can be adjusted. (To find out more about plucked strings and percussion instruments read the article What makes an object into a musical instrument?)
A bowed string is different. A note on a violin can be sustained for as long as your bow-stroke lasts, with a steady amplitude. Although energy is being dissipated into sound and heat, somehow the bow is supplying additional energy at exactly the right rate to compensate. This is one identifying sign of a non-linear system, for which the idea of adding contributions from different vibration modes cannot be applied in the simple way described above. The theory of such systems is always more intricate, and there is scope for very complicated outcomes and chaotic behaviour (read more about chaos in Issue 26). The range of good and bad noises which can be made on a violin string are examples of these complicated outcomes. The same general comments apply equally well to other musical instrument capable of a sustained tone such as the woodwind and brass instruments.
The motion of a bowed string
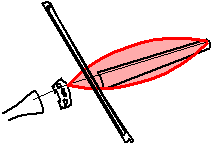
The string appears to vibrate in a parabola-like shape...
So how does a violin string vibrate? This question was first answered by Hermann von Helmholtz 140 years ago. When a violin is played in a normal way to produce a conventionally acceptable sound, the string can be seen to vibrate. To the naked eye, the string appears to move back and forth in a parabola-like shape, looking rather like the first mode of free vibration of a stretched elastic string.
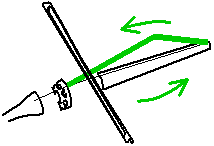
... but it actually moves in a V-shape.
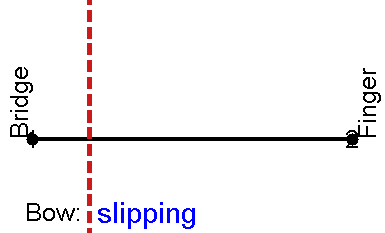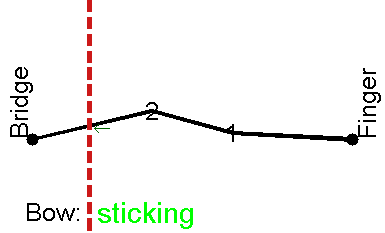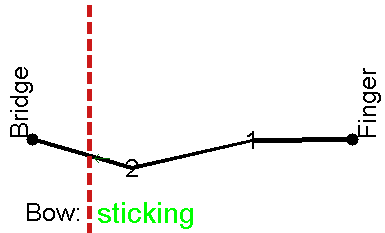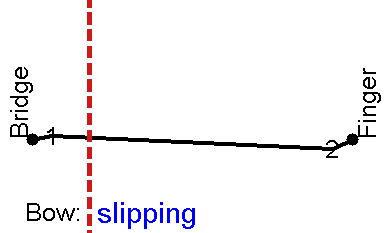
However, upon closer inspection, Helmholtz observed that it moved in a very unexpected way: the string actually moves in a "V"-shape, i.e. the string gets divided into two straight portions which meet at a sharp corner. The fact that we see a gently curving (parabola-like) outline to the string's motion with the naked eye is because this sharp corner moves back and forth along this curve. Hence we only normally see the "envelope", or outline, of the motion of the string.
This motion, called Helmhotz motion is illustrated in this animation:
Helmholtz motion
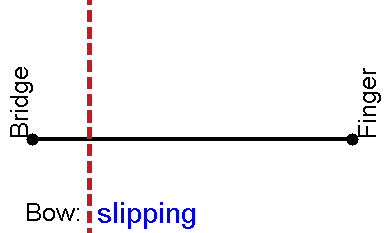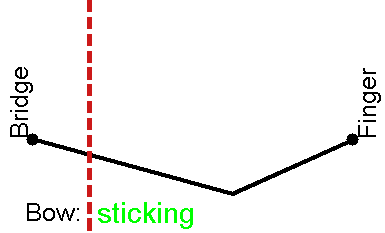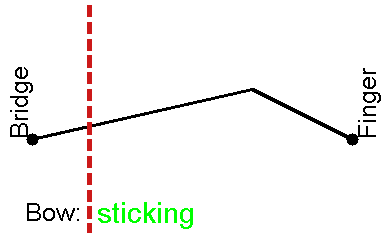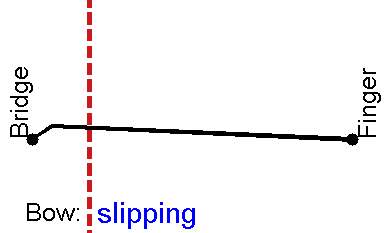
The vertex of the V, called the Helmholtz corner, travels back and forth along the string. Each time this Helmholtz corner passes the bow, it triggers a transition between sticking and sliding friction: while the corner travels from bow to finger and back, the string sticks to the bow and is dragged along with it; then the string slips along the bow hairs (travelling in the opposite direction to the bow) while the corner travels to the bridge and back. The alternation between the two kinds of friction supplies the non-linear element to the system. (Find out how to observe the Helmholtz motion for yourself.)
If the violinist doesn't press hard enough with the bow, then instead of Helmholtz motion the string may move as shown here:
Double slipping motion
There are now two travelling corners on the string, and there are two episodes of slipping per cycle of the vibration. The result is a note at the same pitch as the Helmholtz motion, but with a different waveform and a different sound. For whatever historical reason, this sound is not regarded as acceptable, at least by Western classical violinists. Your violin teacher is likely to dismiss it as "surface sound", and tell you to practise more until you learn not to do it. The switch from Helmholtz motion to this double-slipping motion sets a minimum acceptable level to the bow force, the force with which the bow is pressed against the string.
There is also a maximum acceptable bow force. If the bow is pressed too hard, instead of a musical note the violin may produce a raucous "graunch" noise. The vibration of the string is no longer regular, but switches to a chaotic pattern. Needless to say, this sound is also disapproved of by violin teachers.
But bow force is not enough
The conditions for minimum and maximum bow force can tell us something interesting about the difficulty of playing the violin. When a simple analysis is done of these two conditions, it turns out that they both depend, among other things, on the position of the bow on the string. Suppose the length of the string is $L$, and that the bow is applied a distance $\beta L$ from the bridge, where $\beta$ is usually a rather small number for normal violin playing. Then it can be shown that the maximum bow force is proportional to $\beta^{-1}$, while the minimum bow force is proportional to $\beta^{-2}$. These two conditions can be combined in a graphical form first suggested by John Schelleng in the 1960s. It is most convenient to plot the bow force $N$ and the bow position $\beta$ on logarithmic scales, so that the two power-law relations become straight lines. The diagram then looks schematically like this:
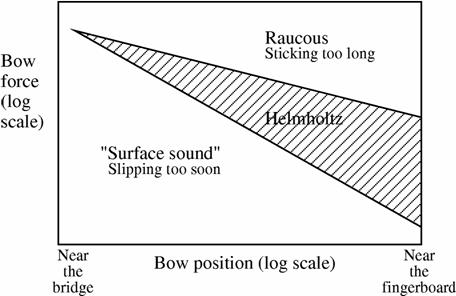
The Schelleng diagram of bow force versus position for a long steady bow stroke
The shaded wedge shows the region within which Helmholtz motion can be achieved. Outside that region, the string does one or other of the undesirable things described above. It is immediately clear that it is easier to produce Helmholtz motion if the bow is away from the bridge: if the bow is too close to the bridge, the two force limits converge and it might not be possible to achieve Helmholtz motion at all.
But the picture reveals something else which is relevant to beginners on the violin. When you first try to play, you have many different things to think about: controlling the bow to touch the correct string, adjusting your left hand to finger the correct note, and so on. It can therefore happen that a beginner does not pay much attention to the position of the bow on the string, $\beta$. In other words, a beginner may move randomly along a more-or-less horizontal line in the Schelleng diagram. The shape of the Helmholtz region in the diagram immediately reveals that this could lead to falling below the minimum force line or rising above the maximum force line, even without the bow force being varied.
Playability
Of course, this is not the whole story about why the violin takes such a lot of practice in order to learn to play it well. The Schelleng diagram really only tells us about the possibility of obtaining Helmholtz motion during a long, steady bow-stroke.

But will I get Helmholtz motion?
But violinists don't just want to play long, steady bow strokes. For musical purposes a wide variety of different bowing gestures are used, such as martelé (hammered bowing with a sudden release) and spiccato (rapid detached notes with the bow bouncing off the strings). A more advanced player will be interested in questions like "If I perform such-and-such a bow-stroke, will I get a Helmholtz motion? How long will it take to become established?". The second question is particularly important, because there is usually a transient period of non-regular motion of the string which may make the start of the note sound scratchy. A good bow gesture will minimise the length of this transient period, and establish Helmholtz motion quickly to give a crisp-sounding note.
This leads to the idea of playability of an instrument. Everyone knows that some violins are a great deal more valuable than others. Why does this happen, when all normal violins appear to be very similar? One aspect of this is "beauty of sound" from the instrument, which is very difficult to address in scientific terms because you first have to find out what a listener means by beautiful sound. However, if you watch a violinist trying out instruments, you may hear comments like "I don't really like the sound of this one, but it is very easy to play", or "This one sounds good but it is very slow to speak". Players are not only interested in sound quality, whatever that may mean precisely, but they are also interested in ease of playing - the playability of the instrument. If one violin is more accommodating than another, in terms of producing Helmholtz motion more reliably or faster, then that violin is likely to be preferred by a player.
Virtual violins
Unlike beauty of sound, this issue of playability lends itself to scientific investigation using mathematical models of a bowed violin string. Over the last 30 years increasingly sophisticated models have been developed. These models are too complicated to solve by pencil and paper mathematical methods, but they can be used to produce computer simulations of how a string on a particular violin will respond to a certain bow gesture. The models can explain a lot of the complicated things which a violin string can do, and they are beginning to be good enough to use to explore design questions: how could the design of a string, or bow, or violin body, be modified to improve the playability?
In a curiously circular way these theoretical models are also being used directly to make music. As computers have got faster it has become possible to run increasingly sophisticated simulation models in real time, to make "virtual musical instruments", where a mathematical model of an acoustic instrument is used as the basis of an electronic instrument (read more in our interview with an Audio software engineer in Issue 27). Some of the most expensive musical synthesiser systems use this approach, in what is called physical modelling synthesis.
Considering the complicated way in which a bowed violin string vibrates, it is not surprising that the violin is a difficult instrument to learn. There is a fine line between achieving Helmholtz motion and creating unacceptable surface and raucous sounds, whether you are just learning to play or are tackling the more advanced bowing techniques. But there is hope for those who have never learnt play the real thing: mathematical models of the physics of a bowed string may allow you to play a virtual violin after all.
About the authors
After a first degree in mathematics at Cambridge, Jim Woodhouse did a PhD on the acoustics of the violin, in the Department of Applied Mathematics and Theoretical Physics at Cambridge (this work being inspired by a hobby interest in building instruments). He then worked for an engineering consultancy firm for a few years, on a variety of problems in structural vibration, before joining the Engineering Department of the University (in 1985) as Lecturer, then later Reader and Professor. His research interests all involve vibration, and musical instruments have continued to form a major part.

Paul Galluzzo studied engineering as an undergraduate at Cambridge University, specializing in fluid dynamics. He is also a keen violinist, with vast experience performing in various countries. Pooling these engineering and musical backgrounds, he subsequently did a PhD on the acoustics of the violin at Cambridge University, specializing in the mechanics of bowed strings. He currently works for an engineering consultancy firm, in various fields involving mechanics and fluid dynamics, and is also involved with work in physiology and electrochemistry. He was recently elected to a Fellowship of Trinity College, Cambridge.
Comments
Anonymous
Great article! As a mathematician who used to play the violin I must admit to never enjoying the sound I made, so gave up after getting to grade 7. I would much rather listen to Itzhak Perlman doing it right! The bowing was never a problem to me but the vibrato on the sustained notes makes such a difference to a whether you get a flat sound or a sonorous one. I would be interested to hear more of the mathematics of vibrato. As with bowing it has boundaries. Too much vibrato disrupts the note but none makes for a dead sound.
Confidence has a great deal to do with the sound a violinist makes. A fear of hitting wrong notes with gusto leads to timid bowing and all of the consequences you so eloquently explained in your article.
Anonymous
The vibrato technique used in violin and human voice performance improves the musical consonance of the resultant sound wave by causing a continous ripple in the intonation of a musical interval about its nominal value. Music is essentially critically unstable digitally processed information controlled by a musical beat that is always present when sound waves interact. It also explains why multi string instruments like 12 string guitars and triple stringed musical notes on a piano sound so good.
John Winter winterjr@tiscali.co.uk
Anonymous
Like sung notes, string vibrato generally grows in both depth (distance from the original pitch) and speed (frequency of oscillation). But that's controlled by the performer, so the "mathematics" isn't driven by anything nearly as the bow/string/body interaction.
The position of the finger on the string changes (it's a rolling motion), which changes the length of the vibrating string. Shorter string length results in a higher pitch, while longer string length gives a lower pitch. The actual motion may come from the arm, wrist or finger (thus "arm vibrato", "wrist vibrato" and "finger vibrato"), but the physics of it at the contact point is essentially the same.
Unlike vibrato with other instruments, string vibrato doesn't go higher than the the original pitch - only lower, and then back up to pitch. The explanation usually given is this helps hear the top frequency as being stable. Going over the original pitch gives the note a sort of "wobble". It's not clear why this isn't the case for other instruments.
Anonymous
"Anonymous" is incorrect--studies show that vibrato goes equally above and below the pitch center on a stringed instrument. Many players and teachers have confused the physical feeling of the direction of the vibrato impulse (which on the violin is away from the body and hence toward the lower side of the pitch) with the actual motion of the fingertip at the point of contact with the string.
Anonymous
It's very interesting! Could You please indicate some study about this topic? Thank You very much!
Anonymous
i play the cello for 6 moths and this made me wonder and the applied mathamatics in the two insturmetns the same
Anonymous
Yes, as far as the bowing of the string goes, all bowed instruments are pretty much the same. Not just the violin and cello, but also more exotic things like the Chinese erhu all work in more or less the same way. There is only one really important difference between the violin and cello from the player's perspective: cellos are more prone to "wolf notes". This is a phenomenon which occurs when you try to play a note which coincides with a very strong resonance of the instrument body. The body vibration can be so strong that it interferes with the bowing, and in extreme cases causes a kind of "stuttering" sound. If you scaled a violin up to make a cello, and you kept to strict proportions with the tuning difference, the cello would be too large to play. So standard cellos are rather undersized. That means you need heavier strings, and a small body which needs to made thinner to keep the resonances in the right place. That combination of heavier strings and lighter body makes the wolf problem much worse, and most cellos suffer from it to a greater or lesser extent. Try searching around F sharp, especially high up on the C string. You will find a resonance around there,and if you try to play that note quietly you may get the wolfy stuttering.
Jim Woodhouse
Anonymous
I'm preparing to start learning to play the violin myself. With so many things working against you, knowing the info you presented here will make it a fraction easier. Also, while I don't have a strong background in physics, I just wanted to say that I found this very interesting. Is the V-shape of the wave pattern (or motion of the string or w.e.) a result of the bow pulling on the string? And what is the 'slipping'?
Anonymous
Great article. I am interested in the tone made by folk fiddlers, some of whom go for a different tone from that used by classical violinists. As a (struggling) fiddler it seems to me that Scottish fiddlers use a classical approach to tone. Long strokes, medium pressure. Irish fiddlers, and to some extent oldtime and bluegrass fiddlers seem to skate over the strings more. Less pressure and very short use of the bow. However, I have recently seen one or two English fiddlers using short bow and more pressure, so the tone is different again. What singers sometimes refer to as a 'closed onset'. The other thing that seems to make a difference is the pressure of the left hand fingers. Assuming you get perfect synchronisation between the bow and the fingers there is still a matter of taste and technique in how hard the string is pressed against the fingerboard. Keep up the good work.
Anonymous
As a professional violinist and a violin teacher I found this extremely well written and accurate. Thanks for the great work!
Anonymous
I goggled guitar vs. violin in order to learn more about stringed instilments (and found this site). I am fairly familiar with the guitar; however have a great interest in the violin. (This specifically came from A Vivaldi – Winter movement 1) Hearing and watching the same song being played on different instruments (Guitar by an unknown performer and violin by Itzhak Pearlman) one unfamiliar with classical music can really gain a new appreciation. I found your information incredibly interesting and insightful to my cause.
Anonymous
Yes violin is harder to play in the beginning, but in the end, the guitar in my opinion is a more difficult instrument to play well. This is because with the violin there are less strings, and a few ways to play the instrument. However the guitar has far more ways to play the instrument to produce different sounds and increase difficulty. You can bend the strings, slide, use a "slide" for a steel guitar effect, whammy bar, pull offs/pull ons, harmonics, pitch harmonics, pick sweeping, tapping, finger styles, slap, chicken picking. Each technique acquired is like learning a different instrument, now combine them all together, that takes a lot of practice.
Anonymous
To the comment posted on March 27, 2011.
The article only covered one small part of the multitude of techniques that are necessary to learn in the violin family of playing. Violin also can slide, they use their own vibrato instead of cheating and using a whammy bar, harmonics exist on the strings, artificial harmonics also exist, etc. For every technique you have to learn, we have to learn another also (I play cello). Please don't be so ignorant and post messages like that. Did you really think every technique possible on the violin family was expressed in this one article?
Anonymous
I have heard some world famous guitarists playing some very difficult, rhythmic and beautiful pieces. But before you write the violin off because it only has 4 strings, please consider how those strings are played. If you really want to get it, get 3 recordings of world class violinists playing pieces like the Bach double violin concerto the Beethoven concerto. I think you have underestimated the dynamic range of the instrument, its ability to convey emotion, the nuances of bowing, trills and a score of other elements.
Anonymous
Dear Jim Woodhouse and Paul Galluzzo ,
The article titled "why is the violin so hard to play" is really wonderful and many thanks for the same.
I have tried to play the violin, Guitar and the piano and find the limitations and difficulty are based on the capacity and passion of each individual. Sight reading is most difficult in the piano and demanding.
Many do not know how to bring out the dynamics and still could pass off as a pianist in the presence of a musically naive audience .
Guitar was the easiest to impress ,within a few weeks of picking up the instrument. However to play like the greats such as Chet Atkins is another story.
The violin seems to be easy if you do not do not know what to expect from it. The tones produced varies from country western through jazz ,Irish and classical western. Not forgetting Chinese ,Indian [South and Hindustani] .Getting the tones was what I found difficult and took me years. I still do not know if I am doing it well as there are not many trained in the kinetics of violin playing enough to correct me. Also getting a good violin bow strings and rosin is very important.
I am not sure how the production Helmholtz motion would modify, or be required for, each of the style mentioned.
David.
Chennai. State of Tamil Nadu.
India.
Anonymous
It was great to understand your analysis.
I always felt there was a point of resonance where the instrument started making a much more beautiful sound. In my mind it had to do with what the sound waves were doing inside the body of the instrument, and not with the physics of the string, until I read your analysis.
I heard a famous soloist playing a Strad in a solo with the Philadelphia Orchestra and talent, genius, 20 years to a lifetime of study, and being able to walk on stage all play a part.
Rosen, type of strings, pressure on the strings, acceleretion, deceleration of the bow--there are so many variables. None of this is news.
Does this phenomenon vary with loud vs. soft playing?
I believe I understand your diagrams, but it appears that the finger is fixed when in fact it is moving up and down the string, creating harmonics, and generally being terribly busy. Is the phenomenon stable in the midst of this?
After you stop there is a residual sound audible, which for lack of a better term I called violinecho, which must be ongoing as we play. How do you account for this.
I hope to here your thoughts on these things, and bravo for your discovery. Is there a Nobel prize in music?
Anonymous
Certainly the player's finger are busy. But the string is vibrating a few hundred times a second, so compared to that even a virtuoso's fingers move pretty slowly. Every note, more or less, the player is aiming for Helmholtz motion. When you do a big finger movement or change bow direction there is a transient time while the string sorts itself out, and learning to keep those transients short is one of the reasons for hours of practicing.
As for the "echoing" sound when you stop: there are several ingredients. If you lift the bow off the string, the string can carry on vibrating much as it would in a pizzicato note. If you stop the string you were playing, the OTHER strings may carry on ringing a bit, in "sympathetic vibration". If you stop all the strings, there is a (much shorter) residual vibration in the violin body: the kind of thing you can hear if you tap the violin bridge (carefully) with a pencil. Finally, there may be an actual echo, from the room you are playing in. Some of those things are going on all the time as you play: but the first one would be killed off if you play your next note on the same string.
Anonymous
.. enjoyed this article - lucky for most musicians they don't have to understand this to create beautiful sounds (actually I don't like even 'well played' violin music as a rule). Otherwise we'd have a very reduced number of capable players..
A 'Cellist (!)
Bruce Jerrick
No, a musician doesn't have to undertand all of the physics involved, but knowing the conclusions -- the effects of bow position and pressure, etc. -- would surely help in pointing the way to just what needs to be achieved to produce a decent sound. Otherwise, it's just "practice 'til you get it right".
Anonymous
This explanation helps me to understand the complexity of bowed instrument playing. I grew up with a sister who practiced the violin quite a bit and it rarely sounded good to me, and I ended up playing the French horn. People speak of the horn as being very difficult to play, and we are dealing with many variables there, too, while producing a good, round tone.
There is no comparison between the two, though. The violin seems infinitely more difficult to play well.
Personally, then, I'll stick to the horn.
The only problem is that now my wife is taking up the fiddle. She is a true beginner. Here we go again. I think that she needs a private practice room away from other human ears, but I appreciate that she's giving this a try..... Her first lesson is on Monday.....
Anonymous
Thank you, Dr. Galluzzo, for your explanation of the violin string's behavior under certain conditions. I am one, who has always enjoyed listening to well played violin music, but knew nothing of the Helmholtz principle, nor have I any experience in stringed instruments. Your explanations were somewhat easy for me to understand, to the extent that I have formed a greater appreciation for those who attempt to play, and more so, for those who play well.
God Bless,
Rick L.
Anonymous
I want to make an apology to Dr. Jim Woodhouse, in my omission of his contribution to this fine article.
Sincerely, Rick L.
Anonymous
I notice that neither authors actually play BOTH the guitar and the violin. This is a crucial weakness in their argument that the violin is "so hard to play" as compared to the guitar. Here, I attempt to highlight the skills that are required to play at a high technical level for both violin and guitar- restricting comments to the genre of classical music as performed on either instrument. I personally perform at an intermediate classical level with both these wonderful instruments. With the violin- as noted by the authors, bow technique is paramount. Any deviation from consistent technique is immediately apparent. The pitch range and physical dimension of the full size violin is however far more "manageable" than that of the guitar with say 15 frets and six strings. There are simply many more variations of note and scale positions compared with those of the violin! Classical plucking technique with guitar is (in my experience) one of THE MOST challenging motor skills to perfect. One is required to perfect EXTREMELY complex independent right hand finger movements ( thumb, index, middle - and some performers include ring and little finger too)- while simultaneously maintaining fluidic, precise placement of the left hand fingers (index, middle, ring, little). In essence, one multi- tasks very complex motor skills at a very rapid tempo - using both dominant and non dominant hands! Combined with the need to develop motor memory for the position of every possible note position on the fretboard makes mastery of the classical guitar a skill at least AS "difficult" (if not more so) than that of classical violin.
Here I DO NOT refer to chord progressions as played on guitar. These techniques are fairly easy to master. I note however that chorded music scores are NOT the norm for violin - the arched design of the neck makes bowing chorded structures very limited in practice!
All said, both violin and guitar are technically very "difficult" instruments -when played according to classsical styles. The rewards these offer however, are enormous! I can only but recommend that one surrenders to both!
jimwoodhouse
The points made in this comment are fair, but really this was not what we were trying to talk about in the article. More or less by definition, a virtuoso performer on any musical instrument is doing things at the limit of human abilities. Most players can't match the experts, so in that sense every instrument is "hard to play". We were trying to make a different point relating to the underlying physics. A complete beginner can pluck an open guitar string or bow an open violin string. The guitar string can be more or less guaranteed to make a musical note with the expected pitch, but the violin string may produce a horrible squawk: the physics of bowing allows a wider range of possible responses than a plucked string. The player has to learn to control these, in a way that has no direct analogue with controlling a single note on a plucked string.
Anonymous
I agree with Mr. Woodhouse on this. I also play violin and guitar, though probably not at your level. However, the point can be generalized to this. Some instruments are easy to get good sound out of- guitar, piano, but others are difficult to get good sound out of- violin, flute. Being a longtime player of guitar (43 years) and violin (23 years) I can tell you this about the two instruments.
The guitar is very easy to get moderately good on. Anywhere you play on the fingerboard, you are guaranteed good intonation, if your instrument is set up well. Many common chords are easy to form and finger. However, at an advanced level, it is extremely difficult to find your way around, especially in improvisation. The guitar is laid out in an illogical way- 4th, 4th, 4th, 3rd, 4th (low to high). To know where you are in a particular scale at any one time is extremely difficult and requires a very deep knowledge of the fingerboard. Arranged music, like classical guitar can be worked out, fingered for convenience or timbre and practiced until memorized. I did this many years ago when I played Scott Joplin rags, then later when arranging swing and jazz music for fingerstyle guitar. Keeping horizontal lines flowing smoothly is a fine point at a high level. See 'Parkening Plays Bach'.
The violin on the other hand is difficult to get a good sound, initially. Later, it can even be difficult to get consistently. As you play in different areas of the fingerboard, good intonation is not guaranteed without a tremendous amount of practice. Also, the further up the neck you play, adjustments must be made in bowing to achieve a good sound. However, the violin is laid out in a very logical way, ascending 5ths. This makes finger and knowing where you are in a scale very easy. I am amazed that there aren't more accomplished jazz and blues violin players. See Darol Anger and Heather Hardy.
Just my $0.02
John Mahony
Anonymous
I appreciated your analysis very much. I do take some exception to the idea of "a sharp corner" moving along the string.
In my experience, the material "stiffness" of the metallic string on a guitar or violin precludes a "sharp corner", and the string does behave very much like a sine wave--essentially what your linear example predicts. In that regard, and from the viewpoint of a background in electronics, I have observed movement on a metal guitar string excited in such a way as to be vibrating in several harmonically related modes at once, and viewed axially, that its movement describes "Lissajou Patterns"--very similar to what we used to view on an oscilloscope and use to count frequencies.
If on a string of non-metallic material, as on a classical guitar or perhaps a ukelele, the wave form moving along the string does in fact have a "sharp corner", does that not imply a non-sinusoidal wave form similar to an asymetrical sawtooth or ramped wave form? When these forms are consistent and enduring, as from a signal generator or from a perfect violin, they should not be too difficult to analyse mathematically--though I'm not sure what might be learned that the ear does not already tell us.
Thank you for an interesting bit of research.
jimwoodhouse
The corner is not PERFECTLY sharp, of course, on a real string, but it really is a long way from being a sine wave. As you say, bending stiffness of the string stops it having an ideally sharp corner. But there are plenty of measurements of real bowed strings vibrating, and also high-speed videos showing the Helmholtz motion directly.
The motion of a bowed string brings in different physics from the vibration of a plucked string such as a guitar. When you pluck a string you certainly excite many overtones of the string, and these are roughly harmonically spaced, but they each vibrate independently of each other: a characteristic of linear systems. But when you bow a string carefully and steadily the nonlinear interaction with friction at the bow produces a periodic motion consisting of exact harmonics, even though these will not precisely match the natural overtone frequencies of the string. The motion has been analysed quite extensively, and it tells you things about how a player might be able to vary the tone of a note, and how a string-maker might design strings to produce different balances of sound.
Anonymous
Thanks for a great article.
If I'm not mistaken, the double-slipping motion described in the article actually does correspond to an acceptable sound in Western classical violin playing. It is the sul ponticello sound, which is called for by Schumann in his D minor sonata, by Beethoven in his quartet op. 131, and may also have been called for as a special effect by Baroque composers. It's ghostly quality can be accounted for by its weakening of the fundamental and emphasis on upper partials. I wonder, in fact, if there may also be triple-slipping and quadruple-slipping, etc., corresponding to higher partials? The sound gets its name, of course, from playing close to the bridge where it's easy to be outside of the Helmholtz triangle and difficult to be inside of it. However, as the article shows, one doesn't need to be close to the bridge in order to be outside of the triangle and, therefore, produce the sul ponticello sound.
Sul ponticello has an interesting relation to standard violin playing. If one plays sul ponticello and then increases the bow pressure markedly, also with a slight increase in speed, one can literally POP inside the triangle. A popping sound occurs as the string rapidly reorganizes itself from double-slip motion into Helmholtz motion--I assume that the pop is a quick burst of chaotic noise as the string reorganizes itself. My students know these as "ponticello pops" and I believe that they are the explanation for well-articulated slurred string crossings (crossing from one string to another without stopping the bow). The initial sound on the new string is briefly sul ponticello, since the weight of the bow is still mostly on the old string upon initial contact with the new string. This initial sul ponticello is drowned out by the still-full sound from the old string. As the weight of the bow transfers to the new string, the initially double-slip motion pops into Helmholtz motion. This explains how a string crossing, which involves no actual finger attack on the finger board, can produce the same popping sound as a finger attack.
Please let me know if any of this needs correcting. Thank you!
Anonymous
I play the violin and I really did not know it was this complicated to play!!! I now developed a new respect for the violin! It is a really hard instrument to play. by the way, the person who discovered this was really smart
Anonymous
I never knew that the plural of violin is violini. Or maybe that's an exclamation mark. I should get a higher resolution screen. BR
Anonymous
Anyone who has taken thermodynamics knows his name. His accomplishments extend much further than this (I was quite surprised seeing him in this article).
Anonymous
Nice article. I wonder if the Helmholtz motion does anything to explain why a violin can seem to sound lower in pitch than the fundamental pitch of the string. I do not know if this is a right perception or not, but when playing a violin against a mandolin tuned the same, the violin seems lower. (I play mainly with fiddlers, who get a good growling sound - it may be less true for classical players.) Yes I know about the mix of harmonics on the plucked instrument, but it seems to hold even if one plucks in the middle to try to pick out the fundamental. And I think that it is true also if one compares a plucked violin to a bowed one.
Does the Helmholtz motion happen at a lower frequency than the fundamental?
Anonymous
Have you noticed any variation in torsional vibrrations with different sorts of strings, particularly gut strings? When I had my violin adjusted for use with gut strings, I felt this might be the case. You would need presumably to assess the torsional flexibility of different strings. I would have thought a steel E string particularly inflexible, in contrast to a gut E. I have also tried using nylon (harp) strings, which are not good, particularly on high notes, but at least my nylon E string doesn't break, and is easier on the fingers by not cutting in to them!
berndfromhamburg
Thanks for the article and the access to the magazine. You wrote that the Helmholtz motion shows identifying sign of a non-linear system. Is there a proof which shows that the physical correct solution cannot be obtained as a superposition of (sinus) modes obeying a linear wave equations?
Anonymous
Over many years, I have noticed that when the weather is very dry my Violin can sound scratchy, and when the humidity increases the nicer sounds are easier to make. Now, I am not saying that your analysis isn't always accurate, but the way the rosin contacts the string is affected by the moisture content of the air.
And, want to add, I have noticed the same characteristic both in Europe and the Americas.
Thank you
Anonymous
An interesting corollary to your observation which I have noticed is that the climate in which a stringed, and especially, a bowed, instrument is built often corresponds to the climate in which that instrument sounds best. This isn't surprising, since an instrument is typically fine-tuned by its builder to sound its best when - and where - it's built, and it would follow that it would likely sound best when played in similar climatic conditions, especially in regards to humidity. However, I rarely, if ever, see this discussed in print.
Anonymous
I enjoyed reading this interesting article, but I noticed that there are some very important variables that are not addressed: the most important is bow speed. The alternating sticking and slipping that is described is dependent upon the speed of the bow. The ideal speed will correspond to the speed of the vibrating string at that point. A bow placement that is closer to the bridge (node) will require a slower bow speed; as the bow placement distance from the bridge increases the bow speed will need to increase to keep up with the amplitude of the vibrating string further from the node. This third variable (in addition to the two you described in your article) creates an exponentially more complex interrelationship between the bow and the string. These variables are stable for a given string and frequency, but these change often when playing the violin (or in my case, the cello). There are still two more variables that must be accounted for: 1) Whenever the finger is depressed, the vibrating string length changes and the optimal placement of the bow must be changed accordingly. 2) Since the optimal speed of the bow is dependent upon the frequency of the vibrating string, the bow speed must be repeatedly adjusted to maintain the relationship to the frequency of the vibration. Take an oversimplified example where the optimal bow speed of A 110 is 1 foot per second. The bow speed for A 220 will need to increase to 2 feet per second, A 440 will be 4 ft/sec and A 880 will be 8 ft/sec. This can prove to be counterintuitive for a player because it means that very high frequencies are best executed with a very fast bow and close to the bridge, something that we normally avoid because of the node/speed relationship described above. The actual bow speed/frequency relationship is less than the mathematically correct example given because the amplitude of a long, low frequency string is much larger than that of a short, high frequency string. Even these variables are only the basis for the creation of the wide variety of qualities of sound that expressive players use to communicate emotion. More bow weight and slower speed, for example will produce a gripping sound while a faster, lighter bow over the fingerboard produces a purer, more intimate and affective sound.
It makes me smile to think of how wonderfully the human brain is able to constantly crunch all of these calculations and imbue an artist's intuition with a beautiful, expressive bow arm.
Anonymous
.I want to thank everyone for their comments. Not too long ago we went to buy my wife a guitar. Whike the sales associate helped her, I wandered around and came across the violins. I have always appreciated the sounds and little bit of history I know about them. Anyway, I picked one up, grabbed the bow, put the violin to my chin and slowly pulled the bow across. Nice throaty sound. One of the associates walked by stopped and raised an eyebrow. He basically told me it was very hard for someone whos never played before to get a sound like that. Lol. No he didnt try to sell me. Anway, it's 2yrs later and playing the violin has been on my mind like crazy recently. I don't know; the way it works makes sense to me. It feels right. I know nothing about music (playing), but this site made sense to me. Just as it made sense in my head when i pulled the bow across the strings. The angle, the bow pressure..etc. Thank you for this article and thank you everyone for your knowledge! I'm 37 yrs old and I know I have a long road. Keep everyone updated.
Anonymous
Gentlemen,
Thanks for this fascinating and instructive description! Is Helmholtz corner caused by one quick bow stroke, similar to a string pluck, where ( multiple times ) the pulse travels down the wire and reflects back ? E.g., as you illustrate, slipping causes multiple corners, i.e., a corner for each slip or pluck. Reason I'm asking is, if bow is kept steady with no slipping on string , seems that we get a corner lasting as long as bow is placed. How to draw this?
Thanks! Mike
Anonymous
Do you have anything about the right intonation?
Anything argumented mathematically I mean...
Anonymous
It is actually quite easy to get a decent sound with the bow without too much effort. Just bow perpendicular to the string using moderate bow speed about half-way between the bridge and the end of the finger board. I often have beginning students experiment with the relationship of bowing and sound by setting the violin on a table and have them bow from the side standing over the violin.
The difficulty arises when they put the violin under their chins. It is extremely difficult to judge when the bow is perpendicular to the strings from that perspective.
Anonymous
I have walked my students through this article to help advance their knowledge as to how the violin works and how they can think about optimizing the desired tone they wish. The moving diagrams were very interesting to my students. From this , I ask them what they think a certain sound may need to be more beautiful or ... I ask them how is it that the violin just made such a such a sound... What was going on? So gradually they are applying this practical knowledge to their notions of what they think is beautiful. Thank you for going to the effort. I am not a 'math whiz' but I will visiting your site again for my amusement. Linda Ford, a violin teacher
Is it possible to post this to FB?
Anonymous
It's interesting to see the difference in string vibration and the maths and physics behind it. However, I would like to hear the difference between Helmhotz and double slipping surface sound. (I can tell that Tracy's daughter Amy in Coronation Street often slips up but I'd like to know what's what.) Also, are there examples where surface sound (and raucous noise) is deliberately played and actually taken advantage of, thereby enriching the melody?
Anonymous
I'm not sure how to go about adding sound files to an article this old. But for any string player it is easy enough to experience the sounds for yourself by looking at the Schelleng diagram, and then doing the wrong thing: start a nice note, then slide the bow towards the bridge without increasing the bow force, and it will slip into surface sound after a bit. Some of these sounds are indeed used deliberately for special effects: "sul ponticello" playing is exactly what I have just described, light bowing near the bridge. "Sul tasto" is a way to get a different kind of failure of Helmholtz motion by bowing a long way from the bridge. Sustained raucous sound would be unusual, but a soloist trying to make themselves heard over the sound of an orchestra may push close to the limit and get a "borderline raucous" sound. Much more commonly, you can hear a bit of raucous sound at the start of a "crunchy" or "scratchy" note. So depending on whether Amy produces a crunch or a whistle, she is slipping out of the Helmholtz region in one way or another.
Anonymous
It's a very interesting article and I do use it myself, as a violin teacher, to explain to students more about bowing and tone (if they are interested).
It busts the myth about the 'silent bow changes', which are physically impossible as the Helmholtz movement simply has to be stopped and go the other direction.
However very interesting, it does not point out the nr 1 reason why violin playing is so hard...
My students most of the time have a decent basic (!) bowing technique and tone in a couple of lessons. Of course they don't have a professional tone and are not able of more advanced bowing techniques at this point.
The real trouble starts with intonation (playing in tune) and as violinists we can't use frets as the intonation needs to be flexible depending if we play in a certain key, where the melody goes, what the harmonic function is and if we play with an orchestra, pianist or string quartet. All this while learning a 'whole tempered' tuning on the violin is already difficult enough as it is.
Besides that what a lot of students find hard is the multitasking... difficult bowing technique, reading notes, watching a conductor or other players, intonation, rhythm, expression and interpretation and all the other stuff that musicians in general cope with while playing.
Of course every instrument on a high level is difficult. Everybody and monkeys can hit some random keys on a piano and sound in tune with a decent tone, but to play Chopin is a whole different story.
What makes the piano more accessible is that with a little to no basic technique one could still play a simple nice sounding song. Besides that on a piano or guitar one could play a couple of chords and sound good already. However, I hear a lot of piano students hit a 'plateau' after some years and not much of them can go beyond this. It takes a lot of practice hours and good teaching to beat this plateau and get to an advanced level.
With the violin all difficulties are there right in the beginning and for many it takes years to play something that doesn't make people want to put cotton in their ears ;). Let's say the plateau that appears for pianists after some years, is there for the violin right in the beginning.
Al this being said (and I hope I haven't bored you), playing a musical instrument is a learnable skill. There is input (good lessons, practice hours) and a predictable output (play beautifully). Of course to achieve a soloist/prodigy/alien level, a little talent might certainly help.
All the best,
Zlata Brouwer, online violin teacher
Frank Beuken
A while ago, I have been watching the movie Youth, with Michael Caine. A retired conductor. Once he was watching a boy playing the violin. He saw, the boy was left handed. He lifted up his elbow, from his right arm ( bow arm). He played much better. The conductor mentioned, to solve an irregularity with an irregularity. Is this true?
Roger Stimson
I am a professional violinist. This is an interesting article. I was actually searching for the exact reason why it takes slightly longer to truly recognise a very high note than it does a lower one.
Meanwhile, you have one error. It is not pressing hard which causes the bad sound. This is a commonly held misunderstanding. A test was carried out on orchestral violinists. In one hour they used an equivalent number of calories as one would shovelling a tone of coal. A great deal of 'pressure' is used. The raucous noise is actually produced when the bow is travelling too slowly for the weight of the arm, thereby 'cramping' the vibration of the string!
Peter Moomaw
This is an interesting article, but I am confused as to how anything is nonlinear. The motion of the Helmholtz corner looks like it could be the solution to a linear wave equation. Also isn't the sticking and slipping analogous to just repeated plucking of the string in exact sync with the motion of the wave packet down the string? Lastly, I was under the impression that the spectrum of a violin is a harmonic series, which I thought typically indicated that a system was behaving linearly. So I guess my question is: Is this motion the solution to a dampened linear wave equation with a forcing term or not? Also how does chaos come into this? Is there a turbulence before the system becomes chaotic? What does the chaotic state sound like? Is thre a well defined pitch during the chaotic state or is it just white noise?