Imaging maths - Inside the Klein bottle
You can read a briefer introduction to the Klein bottle here.

My first practical experience with a Klein bottle was a failure. When I was still at school I came across a picture of a Klein bottle in a weekly journal. I shared my fascination with a friend who was a glassmaker specializing in physics equipment for schools. A few days later I was a proud owner of a physical Klein bottle, made of glass.
What to do with such a bottle? Why not use it for something? Filling it was not easy, because the water flowing in blocked the air inside from coming out. So I decided to keep the remaining air in the bottle and see how effective the half-filled bottle was as a thermometer. I added a few crystals of potassium permanganate to colour the water and make it easier to mark the water levels on the glass.
View the animated version (997K)
To my delight, this primitive but interesting thermometer did indeed show signs of life during the day. Unfortunately, the next morning was a disaster, with lots of red water poured over my windowsill. It was winter, and the low temperature during the night had compressed the remaining air inside the bottle too much, bringing the water level in the handle below the lower curve, so that more air got sucked in. When the air warmed up again in the morning, the increased volume of air in the body pushed the water level too far up the handle. In those days, I never managed to find stable proportions of water and air, but the picture at the beginning of this article shows a workable configuration.
The Klein bottle was discovered in 1882 by Felix Klein [1] and since then has joined the gallery of popular mathematical shapes known to the general public outside the "ivory tower". The bottle is a one-sided surface - like the wellknown Möbius band - but is even more fascinating, since it is closed and has no border and neither an enclosed interior nor exterior. Following Klein we use visual
models to study this surface.
 |
 |
 |
 |
|
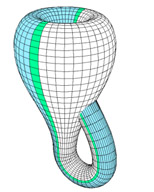
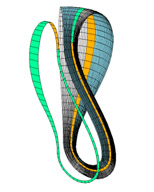
The two Möbius bands of a Klein bottle are connected by an ordinary two-sided |
|||
From the Möbius band to the projective plane
The Möbius band is one-sided - view the animated version (1.3M)
The Möbius band is the simplest one-sided surface, and is easy to make out of a strip of paper. Mark the two sides of the paper - by drawing some red dots on the front and some green dots on the back, for example. Now take two ends of the strip and stick them together after making a single twist in the strip, so that the red-dotted side joins the green-dotted side. This is a Möbius band, and moving along the surface will bring us to each of the red and green dots without us ever crossing a boundary.
The band was discovered in 1858 by the German astronomer and mathematician August Ferdinand Möbius. Adding 0 twists, 2 twists, or more generally, an even number of twists, will always produce a two-sided surface. Similarly, uneven numbers of twists produce various one-sided surfaces. Interestingly, the boundary of a Möbius band is a single closed curve.
Topology is the mathematical discipline which investigates those properties of shapes which do not change under continuous bending and stretching. For example, if a Möbius band is made out of a rubber sheet and we stretch it slightly without breaking it, it will still be a one-sided surface. In contrast, if we had glued the two ends of the strip without first twisting, the resulting cylindrical shape would have been the topologically different two-sided cylinder.
Despite its simplicity the Möbius band was a genuine mathematical discovery. Reasoning about orientability of surfaces is one of the keys to understanding and classifying surfaces and manifolds in topology.
A follow-up task in topology is to get rid of the remaining boundary of the Möbius band to produce a closed surface. The simplest solution would be to use the rubber Möbius band and pull all boundary points continuously together, just as we can pull the points of a circle to a cone. Whether or not we round off the tip of the cone, we obtain a closed surface without boundary, and it is one-sided since from everywhere we can always go to the Möbius band and then switch sides as before. This surface is called the projective plane, and topologically it is the simplest closed one-sided surface. Unfortunately, the geometric realizations of the projective plane are quite sophisticated. For example, it wasn't until 1903 that Werner Boy [17], at the suggestion of David Hilbert (his PhD supervisor at the time), found a geometric realization of the projective plane which has no sharp corners or edges. Fortunately, a different closing of the Möbius band is much simpler to obtain.
The Klein bottle is not a doughnut
One construction of a torus - a doughnut-like shape - starts with a sheet of paper, rolls it up to form a cylinder, and then bends both ends around to close the shape. The inside of the cylinder on one side is connected with the inside on the other side, and the same with the outside. Therefore the torus is a two-sided surface.
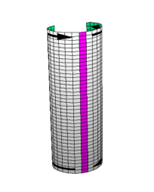
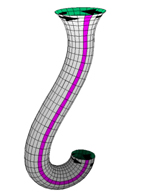
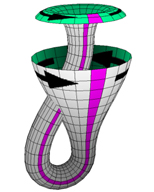
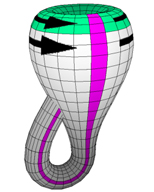
But we could also use the cylinder to make a Klein bottle. Instead of adding a twist, as we did when making a Möbius band from a strip of paper, we loop one end back through the cylinder and glue it to the other end, with the two boundary circles given opposite orientations. To accomplish this with a pleasing shape we adjust the thickness of the cylinder. This allows us to glue inside to outside, and obtain a one-sided surface. In the diagram below we have used white and green to distinguish the two sides of the original cylinder. When the Klein bottle is finished, the colors still show where the cylinder was glued together, but gluing at any other parallel circle would have been just as good.
In his original work [1], Klein introduced the bottle as a "certain unbounded double surface" which "can be visualized by inverting a piece of a rubber tube and by letting it pass through itself so that outside and inside meet".
 |
 |
 |
 |
|
A Klein bottle is formed by joining two sides of a sheet to form a cylinder, then looping the ends of a cylinder back through itself in such a way that the inside (green) and outside (white) of the cylinder are joined - view the animated version (632K) |
|||
Unfortunately, the Klein bottle does not bound a volume - in other words, it has no interior. This means you could put twice as much sugar on a "Klein bottle" doughnut as on a torus doughnut, but it would have no dough inside!
Orientability and one-sidedness
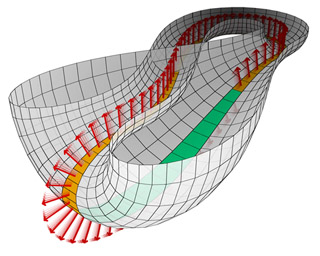
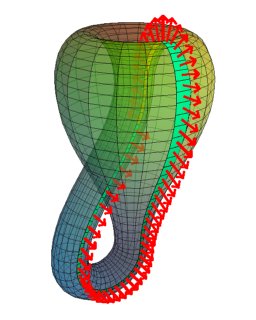
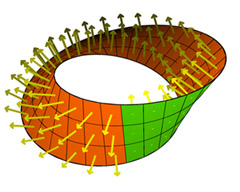
Half of a Klein bottle with Möbius strip - view the animated version (1.3M)
When studying the Möbius band or the Klein bottle, orientability and one-sidedness are important. A surface is one-sided if, standing upright, you can walk along the surface and reach both sides of each point of the surface. Most surfaces in nature are two-sided. For example, the round sphere is two-sided, which ensures that we always walk on top of the earth and never below. Similarly, a wheel-shaped torus, a pretzel, and, more generally, all surfaces that enclose a solid volume, are two-sided.
In nature we do not usually see one-sided surfaces, and remember that the first one-sided surface found by Möbius was an abstract mathematical construction. By drawing perpendicular arrows (normal vectors) along the Möbius band in this illustration of the Klein bottle we emphasize its one-sidedness: by continuous movement we can transport the arrows to both surface sides of a point,
meaning that we cannot distinguish between its front and back. Unfortunately, the very concept of one-sidedness depends on the ambient (surrounding) space - for example, closed curves (loops) in 3-dimensional space do not have sides, although in 2-dimensional space they do.
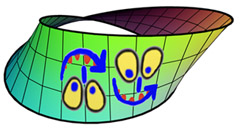
Mirror image and orientability - see the animated version (73K)
A surface is said to be orientable if a shape drawn on it cannot be transformed into its mirror image by simply moving the shape along a path on the surface. Consider the right-way-up face in the illustration. If you move this face around the Möbius band, it returns as its mirror image (and upside-down). This means that the Möbius band is non-orientable. The notion of orientability extends to higher-dimensional spaces, for example, in a non-orientable 3-dimensional universe there would be a way of throwing a right glove so that it returned to you as a left glove!
In contrast to one-sidedness, orientability is an intrinsic property and does not require that a surface is embedded in an ambient space. Since topologists have worked out ways to think about shapes without an ambient space, the notion of orientability is in general much more applicable than that of one-sidedness. Nevertheless, for surfaces in our 3-dimensional world one-sidedness is a
very natural concept.
Mathematical Models

Felix Klein
When Klein became a Professor in Leipzig in 1880, he immediately started to acquire mathematical models and establish a model collection. Klein was a geometer and used these plaster models in his university lectures. Model collections became very popular in mathematics departments world-wide. When he then moved to Göttingen, Klein, together with his colleague Hermann Amandus Schwarz, expanded his new department's collection of mathematical models and instruments so much that at peak times up to 500 models were on permanent display. When you think that a model could cost about £150, this was a major investment in education.
Following the success of mathematical models, in 1893 the Prussian government decided to participate in the World's Columbian Exhibition in Chicago with a university exhibition. Klein and his former student Dyck organized an Exhibition of Mathematics, including about 100 mathematical models and instruments. Production of mathematical models by the publisher Martin Schilling and others stopped in the beginning of the 20th century but many of the plaster shapes are still around in university mathematics departments [14]. Photographs of many plaster models are also available in the internet. Nowadays, repositories like the Electronic Geometry Models journal [15], hosted in Berlin, provide peer-refereed digital models as a source for mathematical experiments.
Make your own...Klein bottles
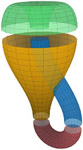
The standard Klein bottle
The standard (Euclidean) Klein bottle can be assembled from four elementary building blocks as shown to the right. Three of the blocks are parts of surfaces of rotation and the vertical blue tube is a slightly deformed cylinder. Stewart Dickson's page [13] shows the assembly in detail.
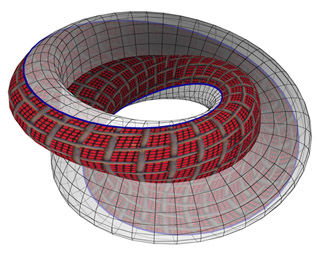
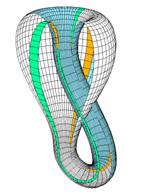
The Figure-8 Klein bottle
The Figure 8-Klein bottle
The Figure-8 surface shown on the left has an even simpler parameterization than the standard Klein bottle. It starts with a planar curve in the xz-plane in the form of an 8. While rotating this curve around the z-axis we add a twist so that the inside is joined with the outside after the loop. Note that the two Möbius bands of this surface are swept out by the crossing of the 8. A Figure-8 curve is given by c(u)=(2cos u, 0, sin 2u), where u runs between 0 and 180o. Applying the rotation and twist we derive the Figure-8 surface:
$ F(u,v)= \left( \begin{array}{c} \sin v (4 +2\cos u \cos tv - \sin 2u \sin tv) \\ \cos v (4 +2\cos u \cos tv - \sin 2u \sin tv) \\ 2\cos u \sin tv + \sin 2u \cos tv \end{array} \right), $
where u and v are both in between 0 and 360o. The parameter t=0.5 determines the twist. The figure above shows how constraining u to the interval [0,180o] or [180o,360o] produces a Möbius strip, shown in red and white respectively.

The Lawson-Klein bottle
The Lawson-Klein bottle
H.B. Lawson came across an elegant realization of a Klein bottle in the 3-sphere S3 among a family of helicoidal - staircase-like - surfaces [12]. The figure on the right shows a projection of the surface into ordinary 3-dimensional space, R3, where the top part of the surface is clipped away to enable an inside view. Along the blue central circle you can see a red and a green Möbius band intersecting, just as in the Figure-8 Klein bottle seen above. By the way, the Lawson-Klein bottle is also a minimal surface in the 3-sphere.
The 3-sphere is the 3-dimensional space consisting of all points at distance 1 from the origin (0,0,0,0) in 4-dimensional Euclidean space. It is a higher-dimensional analogue of the familiar sphere in 3-Euclidean space. And, just as great circles (circles with maximum possible radius) are the shortest routes between two points on the 3-sphere, they also give the shortest routes on the 4-sphere. (Such shortest routes are known as geodesics, and you can find out more about geodesics in Time and motion from Issue 7 of Plus.)
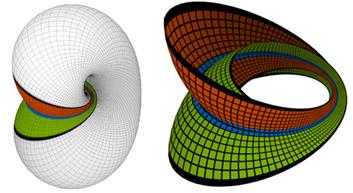
Two Möbius bands on the Lawson-Klein bottle in S3 intersect orthogonally along their base circle
All the grid lines shown on the figure of the Lawson-Klein bottle are great circles, which intersect the blue central circle and which twist when moving along that circle. This spiraling allows a simple formulation of the Lawson-Klein bottle as a helicoidal surface, and other interesting shapes arise when the twist rate is changed. We will devote a future issue of "Imaging Maths" to
un-twisting the properties of twisted "Staircases in Space Forms", with an explicit formula for the Lawson-Klein bottle as a spin-off.
Conclusion

Visualization effect of JavaView
The Möbius band and the Klein bottle were discovered in the 19th century during the search for a classification of surfaces and shapes. Often mathematical shapes are first imagined as a technical tool in an abstract investigation, while some of their beauty remains in the unexplored darkness. From time to time we discover among them a new jewel, a shape in its own right, and then slowly recognize it as a member of an eternal visual repository.
Notes
-
Genuine glass and other real Klein bottles are available from Acme Klein bottle or at the science shop of Spektrum der Wissenschaft, among others.
There are also some strange versions in glass by Alan Bennett. -
Orientability is a binary property of manifolds in any dimension. For example, instead of gluing opposite sides of a square one can pairwise identify opposite faces of a cube. This gives a 3-torus, or, when adding a twist, a 3-Klein bottle. Interested in life in a non-orientable universe? Then watch the video "The Shape of Space" [10].
-
Since the Möbius band is bounded by a single closed curve you might ask if the curve spans a non-orientable soap film when dipped into soapy water. This was answered in the affirmative by a more general construction of W. Meeks, who provided the explicit formula of a minimal Möbius band as an immersion of C-{0} into R3 [16].
-
Lopez constructed a minimal immersion of a 1-punctured Klein bottle into R3 [9]. Since minimal surfaces must extend to infinity, Lopez's immersion doesn't have the nice-looking closed form of the familiar topological immersions. An interesting but open question is whether there exists a compact Klein bottle with constant mean curvature larger than zero.
-
Using a different projection from R4 to R3, G. Francis et al. obtained a shape featured as "Etruscan Venus" [11].
-
The Klein bottle is topologically equivalent to the connected sum of two crosscaps. Therefore the bottle is different from gluing the boundary of a Möbius band with a small hole on a torus. This surface is equivalent to the connected sum of three crosscaps.
- As part of the virtual exhibition "Surfaces Beyond the Third Dimension", Banchoff [4] includes images of the Klein bottle.
-
Background information on mathematical terms related to the Klein bottle and this column can be found at Weisstein's MathWorld [5].
Further Reading
- F. Klein, Über Riemann's Theorie der algebraischen Functionen und ihrer Integrale, Teubner Leipzig (1882), p. 80.
- The MacTutor History of Mathematics archive, Felix Christian Klein, http://www-history.mcs.st-andrews.ac.uk/history/Mathematicians/Klein.html.
- Mathematische Fakultät Göttingen, Felix Klein, http://www.math.uni-goettingen.de/Personen/Bedeutende_Mathematiker/klein.html.
- Thomas F. Banchoff, The Klein bottle, http://www.math.brown.edu/~banchoff/art/PAC-9603/tour/klein/klein.html.
- Eric Weisstein, Klein bottle, http://mathworld.wolfram.com/KleinBottle.html.
- M.C. Escher, Möbius Strip II, Woodcut in red, black and grey-green, printed from 3 blocks. 1963, http://www.mcescher.com/Gallery/recogn-bmp/LW441.jpg.
- The Geometry Center, The Klein bottle, http://www.geom.uiuc.edu/zoo/toptype/klein/.
- M. Gardner, Klein bottles and other surfaces, in Chapter 2 of The sixth book of mathematical games from Scientific American. Chicago, IL: University of Chicago Press, pp. 9-18, 1984.
- Francisco J. Lopez, A complete minimal Klein bottle in R3. Duke Math. Journal, Vol. 71, No. 1, (1993) 23-30.
- Jeff Weeks, The shape of space, Video by Key Curriculum Press, Book by Dekker.
- G. Francis, The Etruscan Venus. In P. Concus, R. Finn, D. Hoffman (Eds.) Geometric Analysis and Computer Graphics. Mathematical Sciences Research Institute Publications. Springer-Verlag, N.Y. 1991. Video by D. Cox, G. Francis, R. Idaszak at http://new.math.uiuc.edu/venus.
- H.B. Lawson, Complete minimal surfaces in S3, Ann. of Math., Vol. 92, pp. 335-374, 1970.
- Stewart Dickson, Topology of the Klein bottle, http://emsh.calarts.edu/~mathart/sw/klein/Klein.html
- K. Polthier, Visualizing mathematics - online, in: Mathematics and Art, C. Bruter (Ed.), Springer Verlag (2002), pp.29-42.
- M. Joswig and K. Polthier (Eds) Electronic Geometry Models http://www.eg-models.de since 2000.
- W.H. Meeks III, The classification of complete minimal surfaces with total curvature greater than -8Pi. Duke Math. J. 48 (1981).
- W. Boy, Über die Curvatura integra und die Topologie geschlossener Flächen, Math. Ann. 57 (1903), pp. 151-184.
About this article

Konrad Polthier is full professor of mathematics at Freie Universität Berlin and the DFG research center MATHEON, and chair of the Berlin Mathematical School. Konrad Polthier received his PhD from the University of Bonn in 1994, and headed research groups at Technische Universität Berlin and Zuse-Institute Berlin. His current research focuses on discrete differential geometry and mathematical problems in geometry processing applications. Dr. Polthier co-edited several books on mathematical visualisation, and co-produced mathematical video films. His recent video MESH (www.mesh-film.de, joint with Beau Janzen, Los Angeles) has received international awards including "Best Animation" at the New York International Independent Film Festival.
Images, animations and applets on this page were produced with the JavaView software (www.javaview.de).
Comments
Anonymous
I design and build exhibits for a museum. I am always looking for ways to engage people in thinking about the how they "see" and "imagine" objects and space. We have a Klein Bottle and some people are able to see that it is not like most objects or surfaces they see in everyday life. Most of those who do understand what is unique about the bottle want to know, "how is it made." I wish that I could get models of your images made! Thank you for a very nice site!
Anonymous
Thank you very much for a beautiful and illuminating page.
I was struggling intuitively with the concept of a crosscap today, while reading this and some similar pages. Do you have a pointer to a URL that could help me? I tried Wikipedia and others but was still left a little confused. Perhaps a crosscap is an entity more difficult to visualise than a Klein bottle?
Is it possible to show how a Klein bottle, such as one of your R^3-embedded representations here, can be "cut up into bits, two of which are crosscaps"? -In a similar manner to the way you show at the top that it can be cut into two Mobius strips and an ordinary annulus-like shape.
Thank you in advance for any help.
Dave (London, UK)
Anonymous
I believe that if you search this concept through wikipedia it will explain your confusion very easily
rodney1956
I love, love. love Mobius loops and Figure-8 Klein Bottles!!! Here are the parts of 3 articles I contributed to http://vixra.org/author/rodney_bartlett which refer to the Mobius and Klein.
-----------------------------------------------------------------------------------------------------
Explaining the “Pioneer anomaly” by refinement of gravitational physics, and related topics ranging from cosmic to human to quantum levels
(1 paragraph)
General Relativity describes gravity and space-time partly by referring to Mercury’s motion. If Einstein’s space-time warping accurately described the motion of the Pioneer probes, we might expect it to conclude that the Pioneers’ reduction in expected distance travelled would be approx. 1 / 30,140 * instead of the actual figure of 1 / 69,032. Rounded to the nearest thousand and inverted, this means the actual warping of space-time has a value of 69 whereas General Relativity gives it a value of 30 (less than half as much – Relativity’s figure is only about 43% of the actual figure, in fact^). This can be explained by warping being based on the Mobius loop. Since one has to travel twice around a Mobius loop to arrive at the same point, the degree of warping is twice as much as it would be in Relativity. This takes us to 86% of the actual value. The foundation of 2-dimensional Mobius loops is then converted into 4-dimensional Figure-8 Klein bottles (see “Mobius loops and Klein Bottles” later in article). Bottles consist of 2 Mobius loops joined on their sides and bottles in motion make up the 3 space dimensions + 1 time dimension of each subuniverse’s space-time. Conversion from Mobius loops into Figure-8 Klein bottles takes energy and could well account for space-time’s warping rising from 86% of its actual value to 100%.
---------------------------------------------------------------------------------------------------------------------------
Intergalactic Plus Time Travel, Hyperspace and Space-Time’s Nature (These Conclusions Address Unusual Things Like Dark Energy by Associating the Work of Einstein, Early Quantum Theorists, Computer Science and Isaac Newton in Unusual Ways.)
(4 separate paragraphs)
1) Discovery.com (March 18, 2010) says: "The universe is not only expanding -- it's being swept along in the direction of constellations Centaurus and Hydra at a steady clip of one million miles per hour, pulled, perhaps, by the gravity of another universe." (this is called “the dark flow”) Could this be describing evidence of an idea suggested by mathematics’ "Poincare conjecture", which has implications for the universe’s shape and says you cannot transform a doughnut shape into a sphere without ripping it. My interpretation follows: This can be viewed as subuniverses shaped like Figure-8 Klein Bottles (above; vaguely similar to doughnuts) gaining rips called wormholes when extended into the spherical spacetime that goes on forever (forming one infinite superuniverse). Picture spacetime existing on the surface of this doughnut which has rips in it. These rips provide shortcuts between points in space and time – and belong in a 5th-dimensional hyperspace. The boundary where subuniverses meet could be called a Cosmic String (the old version of cosmic strings – analogous to cracks that form when water freezes into ice - was first contemplated by the theoretical physicist Tom Kibble in the 1970s). The new cosmic strings are “cracks” in spacetime formed as subuniverses cool, are extremely thin (the diameter of a proton, or smaller), and have immense density (10^19 kg/cm, according to Penguin Encyclopedia, Edited by David Crystal – Penguin Reference Library 2006). This density would vary between any two subuniverses since it depends on the mass and energy content of the boundary regions of the two subuniverses added together, as well as movement of their boundary (the cosmic string) caused by expansion of the subuniverses – because the relativistic motion of each boundary causes enormous quantities of energy to be converted into mass.
2) For simplicity, let’s say the universe is a Mobius loop@ (a Mobius loop can be visualised as a strip of paper which is given a half-twist of 180 degrees before its ends are joined), the twisted nature of a Mobius strip or loop plus the fact that you have to travel around it twice to arrive at your starting point might substitute for the lack of overall spin. Then the cosmos could still function as a time machine. We've seen how it permits travel into the future. We can journey further and further into the future by going farther and farther around the Mobius Universe. We might travel many billions of years ahead - but when we've travelled around the Mobius Universe exactly twice, we'll find ourselves back at our start i.e. we were billions of years in the future … relative to that, we’re now billions of years in the past. (To be strictly accurate, the following references to length/width/height on a Mobius band should refer to those 3 dimensions existing in a Klein bottle, which is an emergent property of combining a couple of 2-dimensional Mobius loops.) The 3 familiar dimensions of length, width and height along, for example, the left side of a loop would have a 4th dimension (time) perpendicular to them (the twisted part at the top). And there would also exist a 5th dimension called hyperspace, at right angles to the 4th and 180 degrees from the length/width/height i.e. on the right. H-space is extended from the side along the loop’s bottom because the WMAP space probe (Wilkinson Microwave Anisotropy Probe) has determined that a very large 72% of the universe is dark energy … and we’ll see later that transmissions of binary digits from hyperspace are an interpretation of dark energy.
@ Actually, each subuniverse in the universe is a Figure-8 Klein bottle: combining 2 Mobius loops in the right way forms a Figure-8 Klein bottle.
(Couldn't insert this diagram at this website)
3) Width a is perpendicular to the length (b or e) which is perpendicular to height c. How can a line be drawn perpendicular to c without retracing b’s path? By positioning it at d, which is then parallel to (or, it could be said, at 180 degrees to) a. d (the spaceship) is already at 90 degrees to length b and height c. To be at right angles to length, width and height simultaneously; it has to also be perpendicular to (not parallel to) a. This is accomplished by a twist, like on the right side of the Mobius loop pictured above, existing in a. Then part of a is indeed at 180 degrees to d, but part of a is at 90 degrees to d. This situation requires a little flexibility or “fuzziness” which allows the numbers to deviate slightly from their precise values of 90 and 180. The fuzziness is represented in nature by past, present, future, space, time, and hyperspace existing everywhere rather than being confined to particular locations. Thus, 90+90 (the degrees between b & c added to the degrees between c & d) can equal 180, making a & d parallel. But 90+90 can also equal 90, making a & d perpendicular. (Saying 90+90=90 sounds ridiculous but it has similarities to the Matrix [of mathematics, not the action-science fiction movie] which is an array of numbers placed in rows and columns. It was worked out in the mid-nineteenth century by British mathematician Arthur Cayley, matrix mechanics is a version of quantum mechanics discovered by Werner Heisenberg in 1925, and matrices say X multiplied by Y does not always equal Y times X. In this paragraph, the first 90 plus the second 90 does not always equal the second 90 plus the first 90 because 90+90 can equal either 180 or 90.) If the infinite universe is composed of subuniverses shaped like figure-8 Klein bottles (diagram at end of paragraph - 2 Mobius loops are joined on their sides to form Bottle), in each subuniverse there would be 2 perpendicularities to the twist (one lot of 90+90, then another 90+90). 180+180 could equal 360 – represented in physics as a subuniverse, a galaxy, or one of the spherical waves above producing quantum entanglement and translating space by 90 degrees. 180+180 could also equal 180 – represented in physics by both of the above spherical waves interacting to produce inversion (translation by 180 degrees) of space which permits the spaceship to enter hyperspace. Since a fuzzily spherical figure-8 Klein bottle is necessary to form (90+90) + (90+90), any spherical or fuzzily spherical thing in this fractal universe (subuniverse, galaxy, black hole, asteroid, subatomic particle, or anything made of either fermions or bosons) would be an example of altered or warped space-time and must include hyperspace in its composition.
4) Now you see why I wrote all that stuff about hyperspace, quantum spin, matrices, Mobius loops and figure-8 Klein bottles: it was necessary to explain travel into the past.
------------------------------------------------------------------------------------------
Whimsical, frivolous title - How ET, or an intelligent robot from the future, might interpret science and maths
More accurate title - reviewing electroweak theory and quarks via Mobius, Figure-8 Klein Bottle, Tegmark's MUH, & revisiting Einstein's G-EM relatedness
(all paragraphs continuous)
Look at the illustration below of a loop (in this case, a Mobius strip). The bottom of it looks like part of a circle while the top has a twist. This particular orientation can be referred to here as “spin 1” – it only looks the same if it’s turned round a complete revolution of 360 degrees, like the Ace of Spades card pictured in “A Brief History of Time”. A photon has spin 1 and when it interacts with a graviton in a wave packet* (gravitons have spin 2 and look the same if turned round 180 degrees or half a revolution, like the double-headed Queen of Spades in “A Brief History of Time”), the particles’ orientations can be the same i.e. they can both have their twist at the top.
* (A wave packet is a short "burst" or "envelope" of wave action that travels as a unit, and is interpreted by quantum mechanics as a probability wave describing the probability that a particle will have a given position and momentum). It acts like 2 hands coming together and catching a ball. Actually, photons are absorbed and emitted just as in laser cooling but instead of a laser beam slowing down atoms, the envelope slows (and traps) photons.
Mobius Loop
If oriented the same way, the electromagnetic and gravity waves forming the wave packets undergo constructive interference and reinforce to produce mass - a massive W+, W- or Z^0 (the carriers of the weak force) that must be turned 360 degrees to look identical i.e. they have spin 1. Slight imperfections in the way the Mobius loops fit together determine the precise nature of the binary-digit currents and therefore of exact mass or charge. If oriented dissimilarly, they undergo destructive interference and partly cancel (there’s little or no twist now – both top and bottom of the new Mobius resemble parts of a circle) to create masslessness - a massless, chargeless gluon (carrier of the strong force) that is identical if turned 360 degrees and similarly possesses spin 1. Quarks – in this interpretation, the gravitational and electromagnetic interference caused by a particular positioning of a Mobius strip - combine into protons, mesons and neutrons but are never found in isolation and cannot be observed directly. (In this explanation, the strong and weak nuclear forces have no existence independently of gravitation and electromagnetism. Since EM is modified gravitation according to this article, it’s perfectly OK to simply say “independently of gravitation”). They could simply be products of graviton-photon interaction: the strong nuclear force - which is 10^38 times gravity’s strength - could be gravity “added to” electromagnetism while the weak nuclear force – 10^25 times gravity’s strength - could be gravity “subtracted from” electromagnetism [identical to the antigravitons of antigravity being added to electromagnetism]. The 2nd example assumes combining with 100 billion antigravitons while the 1st assumes the presence of 100 gravitons per electromagnetic photon, and I believe these “assumptions” are justifiable by photon-graviton oscillation or transmutation …) An antiphoton would be formed by the fitting together of a force-carrying, spin -2 antigraviton with a spin 1 photon. (-2)+(+1) = -1. If it’s correct that “antiparticles are identical in mass to matter particles but opposite in one key property; we would expect the antiparticle of a massless, chargeless photon to have a spin of negative 1.
It has been shown how different spins can be orientations of the Mobius strip. One strip could be called the p (positive) Mobius and another the n (negative) Mobius. Both of these would be purely mathematical^ in nature (after all, a strip is only 2-dimensional and cannot substitute for the physical world). In fractal fashion, they’d be reflected in the world we know as the p-type and n-type semiconductors resulting from the appropriate doping of silicon (adding impurities to alter electrical properties). This is what you’d expect in this electronics-based universe. But as the supplementary matter shows, the strips can be joined on their edges to form a 4-dimensional Figure-8 Klein Bottle. And each Bottle is the 3 space dimensions and 1 time dimension of one of the infinite number of subuniverses making up the cosmos (and also expressing things like 5th-dimensional hyperspace, cosmic wormholes and cosmic strings).
(2 Mobius loops – each one is 2 dimensional - joined along their edges can form a 4 dimensional Klein Bottle)
^ When his paper regarding mathematical formulas creating reality was submitted to a scientific journal and rejected as being too speculative, U.S. cosmologist Max Tegmark showed the rejection letter to his friend John Wheeler (1911-2008), a Princeton theoretical physicist. Wheeler said, “Extremely speculative? Bah!” Then he reminded Tegmark that some of the original papers on quantum mechanics were also considered extremely speculative.
------------------------------------------------ END ---------------------------------------------
HELP!
Hey! Love the information you provided in that comment. I want to use it for school, can you please provide me with the link/book or whatever source this is from...? I need to give citations!!
rodney1956
"Basic Blueprint for Making This Universe" - http://vixra.org/abs/1301.0040
references/more info - including 1) Intergalactic and Time Travel, 2) hyperdimensionality, 3) explaining so-called "anomaly" of Pioneer spaceprobes by refinement of Einstein's space-time warping, 4) interpretation of electroweak unification, quarks and quantum spin in terms of orientation of Mobius and figure-8 Klein, 5) refinement of Newton's gravitation, 6) Theory of Everything and reduction of 4 fundamental forces to one, 7) implications for philosophy, Global Financial "Crisis", and religion
http://vixra.org/abs/1210.0108
http://vixra.org/abs/1212.0096
http://vixra.org/abs/1301.0022
Anonymous
Articles such as this one follow in the footsteps of great educators such as David Hilbert. Your work here might inspire someone to invent a 3D interferometer... and with that comes the discovery of a space-time structure to fit a unified field.
A Mobius band will be oriented either left or right handed depending on which way the 1/2 twist is made. As with a spring, the twist and the closing of the loop locks in energy; in this respect the Mobius band resembles a unit of 1/2 spin (as it pertains to subatomic physics). If we cut this "spin unit" down the middle it becomes a spin of 1 (a full twist). Cutting the band off center makes a spin of 1 and 1/2. Gluing two bands together should make a spin of net zero or plus/minus 1... my math skills fall short at that point.
The Penrose Twistor is envisioned as an nth dimensional extension of vectors & tensors, and seems to become a Mobius/Klein type of topology; this could be the unified field model long sought by physicists, yet the math proved too difficult even for Roger Penrose.
I might have a way of simplifying the math in either case. This requires a redefinition of pi as the square root of 6 times Reimann's Zeta(1) value. However, the term 6 represents a structure of six Klein bottles interconnected/looped at their handles as to form a type of xyz axial system that allows all three axes to represent complex numbered coordinates. This pushes the difficult/impossible math toward the center (at the handles), and makes the exterior (pseudo-spheres of the Klein bottles) as simple as adding complex numbers.
With three values, 81, the speed of light, and a secret "uncertainty" number, I can make this 6-lobed structure mathematically represent any Lepton or Quark (by spin, mass, and charge). Pretty neat, huh? The only great difficulty is finding empirical evidence of such a 6-lobed structure in nature (doh!). That won't happen until someone invents the detector, a similarly 6-lobed interferometer!
rd4ji2@live.com
PS a couple of other difficulties are we need 3.14 space dimensions and the value of pi gets smaller (becomes 2) at the center of the structure.
Anonymous
It occurred to me that a Mobius strip twists through space. However the depicted Klein bottles (except maybe the Lawson one) seem to discard this twist. I've created my own Klein 'strip' that derives directly from a Mobius strip.
You can find images at:
1. http://i57.tinypic.com/mcq3q0.png
2. http://i62.tinypic.com/j5dp4x.gif
3. http://i60.tinypic.com/raytqo.gif
The first one shows the Klein Strip in the classic mobius view.
The second one is an animation which shows how it directly derives from a Mobius strip.
The third one is an animation that depicts how the rotation steps along the Strip.
I hope that these will qualify as Klein shapes especially as they derive directly from a Mobius.